Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Poster: Factorisation
Poster: Factorisation | Mathematics (Maths) Class 8 PDF Download
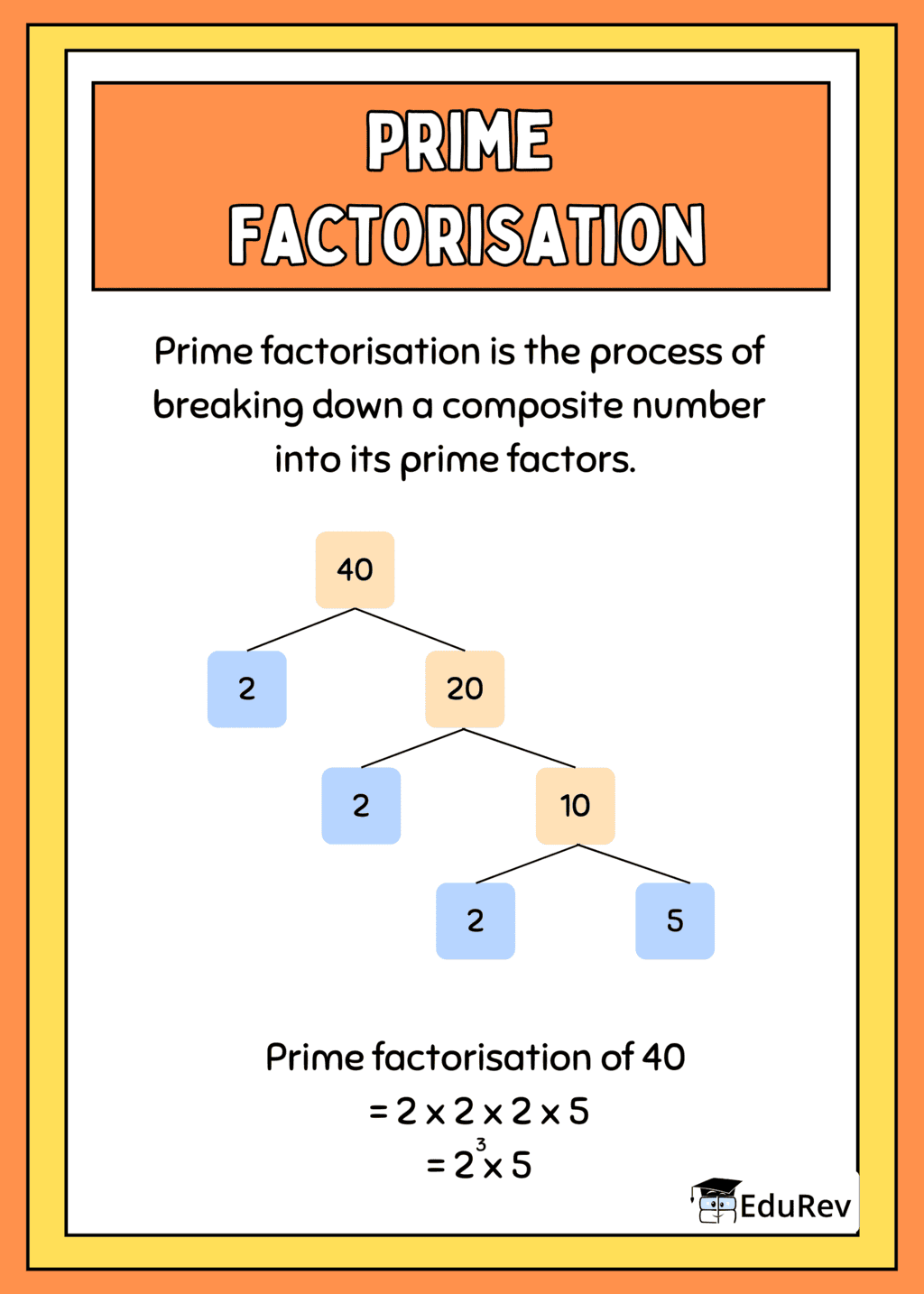
The document Poster: Factorisation | Mathematics (Maths) Class 8 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
94 videos|549 docs|42 tests
|
FAQs on Poster: Factorisation - Mathematics (Maths) Class 8
| 1. What is factorisation in mathematics? |  |
Ans.Factorisation is the process of breaking down an expression into a product of its factors. For example, the factorisation of the quadratic expression \(x^2 - 5x + 6\) is \((x - 2)(x - 3)\). This technique is essential for simplifying expressions, solving equations, and finding roots.
| 2. Why is factorisation important in solving equations? |  |
Ans.Factorisation is crucial in solving equations because it allows us to rewrite complex expressions in simpler forms. By factoring an equation, we can find its roots or solutions more easily, often transforming it into a form that can be solved using the zero-product property, which states that if the product of two factors is zero, at least one of the factors must be zero.
| 3. What are the common methods of factorisation? |  |
Ans.Common methods of factorisation include:
1. Factor by grouping: Reorganizing terms to create common factors.
2. Factoring out the greatest common factor (GCF): Identifying and extracting the highest factor common to all terms.
3. Quadratic factorisation: Applying techniques like completing the square or using the quadratic formula to factor quadratic expressions.
4. Special products: Recognizing patterns such as the difference of squares or perfect square trinomials.
| 4. How can I factor a polynomial expression? |  |
Ans.To factor a polynomial expression, start by looking for the greatest common factor of all the terms. Then, if applicable, identify special patterns (like difference of squares) or use methods like grouping or trial and error with possible roots. For polynomials of degree two or higher, you may also apply synthetic division or the Rational Root Theorem to help with the factorisation.
| 5. What are the applications of factorisation in real life? |  |
Ans.Factorisation has numerous real-life applications, including in areas such as physics for solving quadratic equations related to projectile motion, in engineering for optimizing designs, and in finance for analyzing profit/loss scenarios. It also plays a role in computer science algorithms, cryptography, and data compression techniques, making it a vital skill across various fields.
Related Searches





















