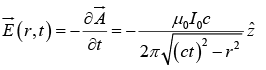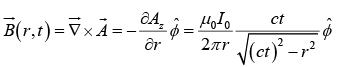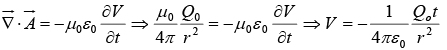Potential & Field Formulation for Time Varying Fields | Electricity & Magnetism - Physics PDF Download

Clear all your Physics doubts with EduRev Join for Free

Join for Free

Scalar and Vector Potentials

We want general solution to Maxwell's Equations,

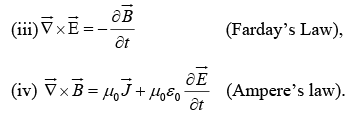
Given 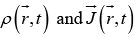 what are the fields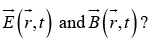

From equation (ii) we can still write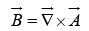

⇒

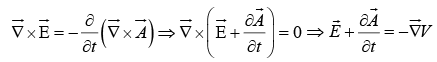
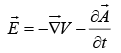
Now from equation (i)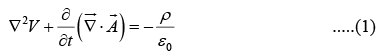

From equation (iv)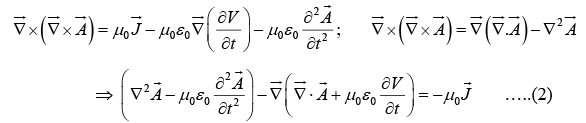

Equations (1) and (2) contain all the information of Maxwell’s equations. Thus we need to calculate only four components (one for V and three for 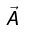 instead of six components (three for  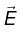and three for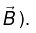

Example 1:  In an infinite straight wire constant current I₀ is turned on abruptly at t = 0 . Then corresponding retarded potentials are given by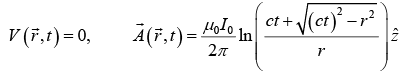 . Find the fields corresponding to these potentials.

The electric field is

And the magnetic field is

Gauge Transformation

Suppose we have two sets of potentials, 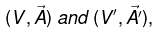 which correspond to the same electric and magnetic fields.

Thus,

Since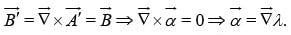

Two potentials also give the same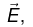
So,


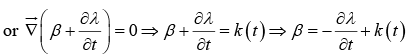
Actually, we might as well absorb k (t ) into λ, defining a new λ by adding 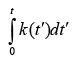 to the old one. This will not affect the gradient of λ ; it just adds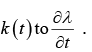

It follows that

Conclusion: For any old scalar function λ , we can add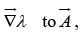  

provided we simultaneously subtract 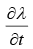 from V. None of these will affect the physical quantities  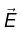and 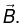 Such changes in V and  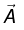are called gauge transformations. 

Coulomb and Lorentz Gauge

Coulomb Gauge reads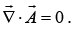

Lorentz Gauge condition is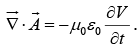

Since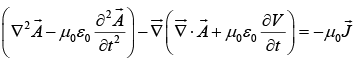

and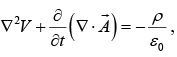

Using Lorentz Gauge condition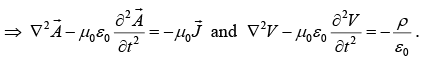

The virtue of the Lorentz gauge is that it treats V and 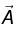 on an equal footing: the same 

differential operator 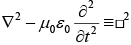  (called the d' Alembertian) occurs in both equations: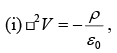



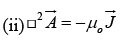
Example 2: For a vector potential 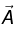 the divergence of  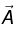is 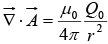 where Q₀ is a constant of appropriate dimensions. Find the corresponding scalar potential  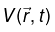that makes  and V Lorentz gauge invariant.