Explore Exams
Login Signup
Sign in Open App
CAT Exam  >  CAT Notes  >  100 DILR Questions for CAT Preparation  >  Practice Question - 79 (Games and Tournaments)

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation PDF Download

The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.

The management of a university hockey team was evaluating performance of four women players - Amla, Bimal, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals.

  1. Only one goal was scored in every even numbered match.
  2. Harita scored more goals than Bimal.
  3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
  4. Bimal scored a goal in Match 1 and one each in three other consecutive matches.
  5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
  6. The match in which the highest number of goals was scored was unique and it was not Match 5.

Q1: How many goals were scored in Match 7?
(a) 3
(b) 2
(c) 1
(d) Cannot be determined

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT PreparationView Answer  Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Ans: (c)
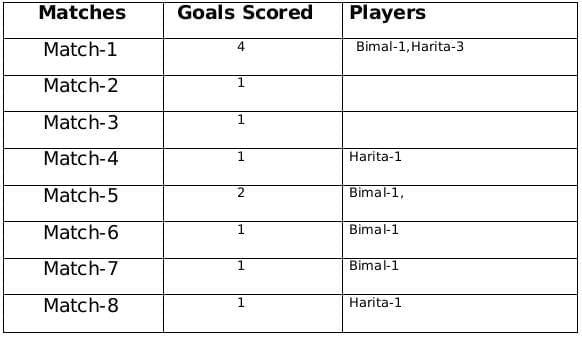
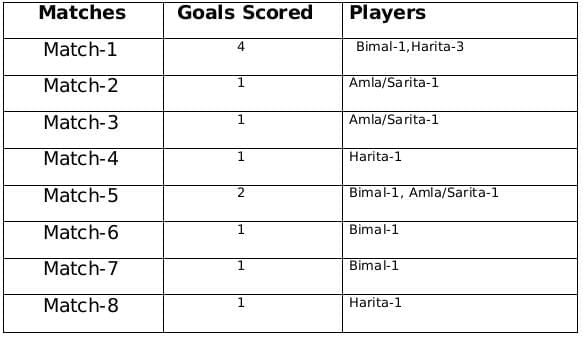
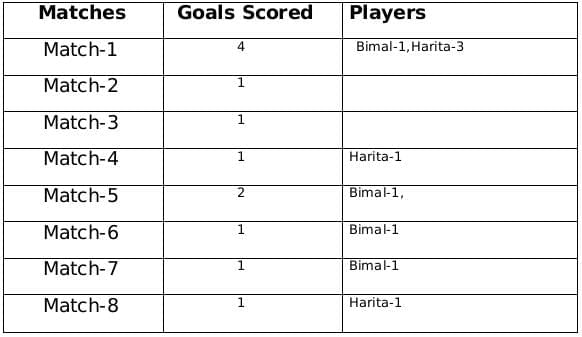
A total of 12 goals were scored in 8 matches and each player scored at least one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

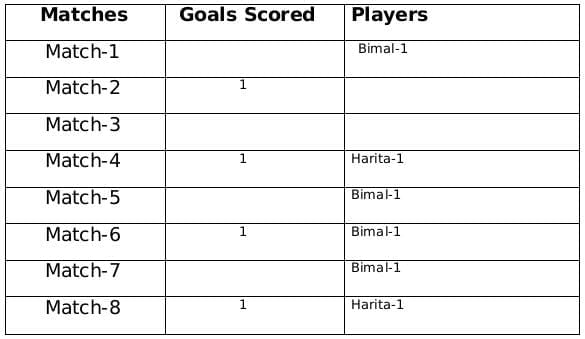
Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1, then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2, then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a = 1, b = 4 and c = 2

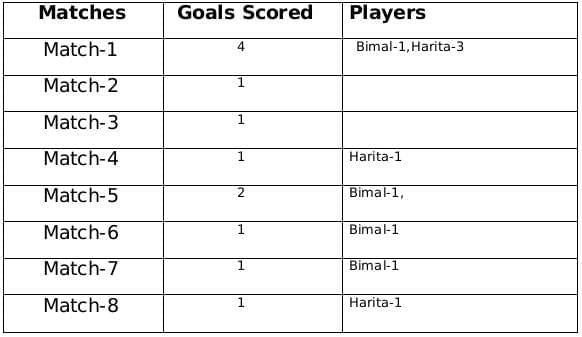
Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Q2: Which of the following is the correct sequence of goals scored in matches 1, 3, 5 and 7?
(a) 5, 1, 0, 1
(b) 3, 1, 2, 1
(c) 3, 2, 1, 2
(d) 4, 1, 2, 1

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT PreparationView Answer  Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Ans: (d)
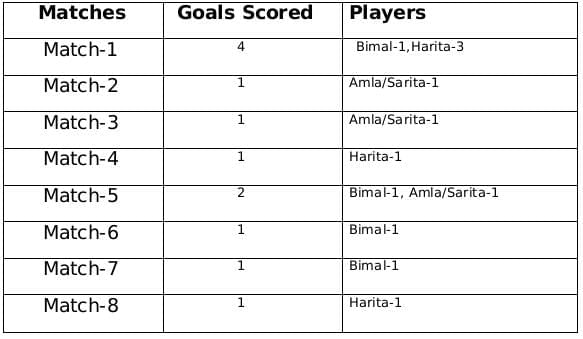
A total of 12 goals were scored in 8 matches and each player scored at least one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

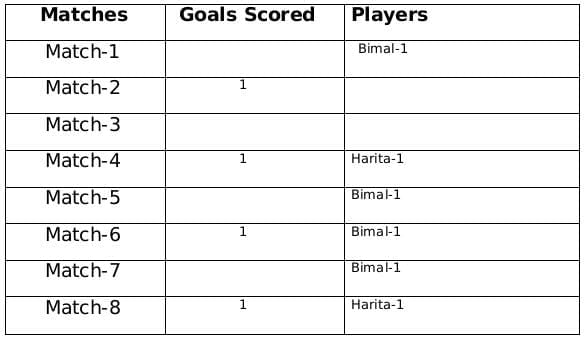
Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1, then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2, then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
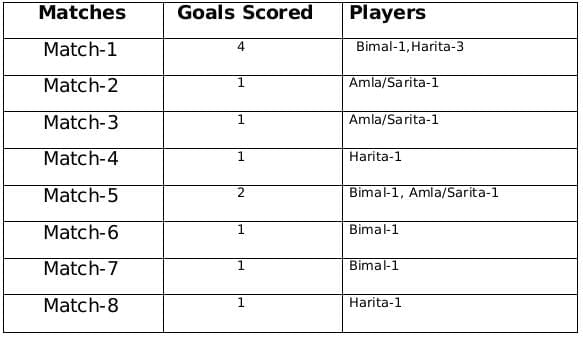
Therefore the only possible solution is a = 1, b = 4 and c = 2

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Q3: Which of the following statement(s) is/are true?
Statement 1: Amla and Sarita never scored goals in the same match.
Statement 2: Harita and Sarita never scored goals in the same match.
(a) Statement-1 only
(b) Statement-2 only
(c) Both the statements
(d) None of the statements

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT PreparationView Answer  Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Ans: (c)
A total of 12 goals were scored in 8 matches and each player scored at least one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1, then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2, then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a = 1, b = 4 and c = 2

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Q4: Which of the following statement(s) is/are false?
Statement 1: In every match at least one player scored a goal.
Statement 2: No two players scored goals in the same number of matches.
(a) None of the statements
(b) Statement-1 only
(c) Both the statements
(d) Statement-2 only

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT PreparationView Answer  Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Ans: (a)
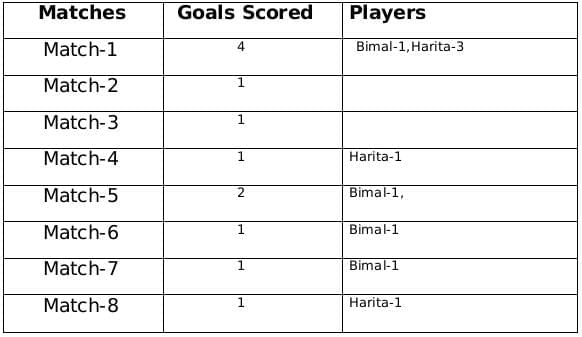
A total of 12 goals were scored in 8 matches and each player scored at least one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1, then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2, then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a = 1, b = 4 and c = 2

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Q5: If Harita scored goals in one more match as compared to Sarita, which of the following statement(s) is/are necessarily true?
Statement 1: Amla scored goals in consecutive matches.
Statement 2: Sarita scored goals in consecutive matches.
(a) Statement-2 only
(b) None of the statements
(c) Statement-1 only
(d) Both the statements

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT PreparationView Answer  Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

Ans: (b)
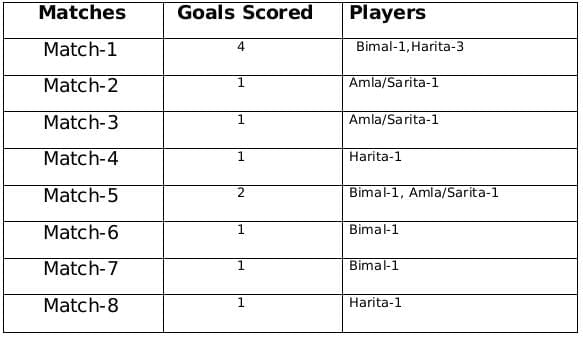
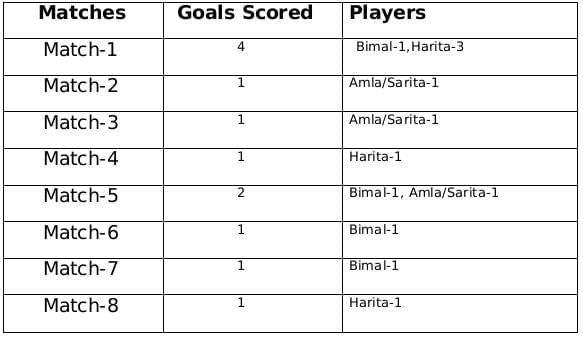
A total of 12 goals were scored in 8 matches and each player scored at least one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1, then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2, then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a = 1, b = 4 and c = 2

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

The remaining 3 goals were scored in the match 2, 3 and 5 by Amla and Sarita in some order.

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

The document Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation is a part of the CAT Course 100 DILR Questions for CAT Preparation.
All you need of CAT at this link: CAT
102 videos|123 docs|121 tests
Join Course for Free

FAQs on Practice Question - 79 (Games and Tournaments) - 100 DILR Questions for CAT Preparation

1. What are the common formats of games and tournaments used in competitive settings?
Ans. The common formats of games and tournaments include knockout (or elimination) tournaments, round-robin tournaments, and Swiss system tournaments. Knockout tournaments eliminate participants after a loss, while round-robin tournaments allow each participant to compete against all others. The Swiss system combines elements of both, pairing participants with similar scores over several rounds without eliminating anyone.
2. How do point systems work in games and tournaments?
Ans. Point systems in games and tournaments typically award points based on performance. For example, in round-robin formats, participants might earn points for wins, ties, or losses, contributing to their overall ranking. A common system awards 3 points for a win, 1 point for a draw, and 0 points for a loss, which helps determine standings and qualifications for subsequent rounds.
3. What is the significance of seeding in tournament formats?
Ans. Seeding is crucial in tournament formats as it determines the matchups based on participants' rankings or past performance. Higher-seeded players or teams face lower-seeded ones in the early rounds, which aims to prevent the strongest competitors from eliminating each other too soon. This system enhances fairness and maintains spectator interest by ensuring that top contenders progress further in the tournament.
4. How do tie-breakers work in tournaments?
Ans. Tie-breakers are used in tournaments when participants have equal points or scores at the end of the competition. Common tie-breakers include head-to-head results, differential points, or additional playoff matches. These criteria help determine rankings or advance participants when standard point systems do not yield a clear winner.
5. What strategies can participants employ to succeed in tournaments?
Ans. Participants can employ various strategies to succeed in tournaments, such as studying opponents' previous performances, managing time effectively during matches, and adapting their gameplay based on the tournament format. Additionally, maintaining physical and mental stamina, practicing under tournament conditions, and developing a flexible game plan can enhance their chances of success.
About this Document
Sep 26, 2025 Last updated
Related Exams
CAT
Document Description: Practice Question - 79 (Games and Tournaments) for CAT 2025 is part of 100 DILR Questions for CAT Preparation preparation. The notes and questions for Practice Question - 79 (Games and Tournaments) have been prepared according to the CAT exam syllabus. Information about Practice Question - 79 (Games and Tournaments) covers topics like and Practice Question - 79 (Games and Tournaments) Example, for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Practice Question - 79 (Games and Tournaments).
Introduction of Practice Question - 79 (Games and Tournaments) in English is available as part of our 100 DILR Questions for CAT Preparation for CAT & Practice Question - 79 (Games and Tournaments) in Hindi for 100 DILR Questions for CAT Preparation course. Download more important topics related with notes, lectures and mock test series for CAT Exam by signing up for free. CAT: Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation
Description
Full syllabus notes, lecture & questions for Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation - CAT | Plus excerises question with solution to help you revise complete syllabus for 100 DILR Questions for CAT Preparation | Best notes, free PDF download
Information about Practice Question - 79 (Games and Tournaments)
In this doc you can find the meaning of Practice Question - 79 (Games and Tournaments) defined & explained in the simplest way possible. Besides explaining types of Practice Question - 79 (Games and Tournaments) theory, EduRev gives you an ample number of questions to practice Practice Question - 79 (Games and Tournaments) tests, examples and also practice CAT tests
102 videos|123 docs|121 tests
Join Course for Free
Download as PDF
Explore Courses for CAT exam
Related Searches

Previous Year Questions with Solutions

,

ppt

,

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

,

Sample Paper

,

Objective type Questions

,

past year papers

,

mock tests for examination

,

shortcuts and tricks

,

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

,

study material

,

Summary

,

Viva Questions

,

Free

,

pdf

,

Practice Question - 79 (Games and Tournaments) | 100 DILR Questions for CAT Preparation

,

Semester Notes

,

Extra Questions

,

Exam

,

practice quizzes

,

MCQs

,

Important questions

,

video lectures

;
Additional Information about Practice Question - 79 (Games and Tournaments) for CAT Preparation

Practice Question - 79 (Games and Tournaments) Free PDF Download

The Practice Question - 79 (Games and Tournaments) is an invaluable resource that delves deep into the core of the CAT exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Practice Question - 79 (Games and Tournaments) now and kickstart your journey towards success in the CAT exam.

Importance of Practice Question - 79 (Games and Tournaments)

The importance of Practice Question - 79 (Games and Tournaments) cannot be overstated, especially for CAT aspirants. This document holds the key to success in the CAT exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Practice Question - 79 (Games and Tournaments) Notes

Practice Question - 79 (Games and Tournaments) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Practice Question - 79 (Games and Tournaments). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Practice Question - 79 (Games and Tournaments) Notes on EduRev are your ultimate resource for success.

Practice Question - 79 (Games and Tournaments) CAT Questions

The "Practice Question - 79 (Games and Tournaments) CAT Questions" guide is a valuable resource for all aspiring students preparing for the CAT exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Practice Question - 79 (Games and Tournaments) on the App

Students of CAT can study Practice Question - 79 (Games and Tournaments) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Practice Question - 79 (Games and Tournaments), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Practice Question - 79 (Games and Tournaments) is prepared as per the latest CAT syllabus.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup