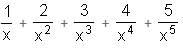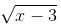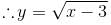This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Functions (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Functions - 1
Try yourself:If f(x) = y and g(x) = y2 + 1, find g(f(x)).
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:If , 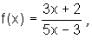 then
then
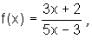 then
then
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:The graph of the function y = 5x6 + 3x4 - x2 + 8
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:If f(x, y) = 3x2 - 2xy - y2 + 4, find f(1, -1).
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:The given graph is


View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:A function is defined as f(x) = 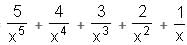 + 1 + x + 2x2 + 3x3 + 4x4 + 5x5. If f(2) = 260.78, what is the value of f
+ 1 + x + 2x2 + 3x3 + 4x4 + 5x5. If f(2) = 260.78, what is the value of f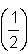 ?
?
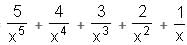 + 1 + x + 2x2 + 3x3 + 4x4 + 5x5. If f(2) = 260.78, what is the value of f
+ 1 + x + 2x2 + 3x3 + 4x4 + 5x5. If f(2) = 260.78, what is the value of f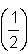 ?
?
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:Find the range of the function f(x) = 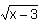
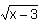
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:f : → R and g : R → R are defined as f (x) = x2 and g (x) = x + 3, x ∈ R, then (fog) (x) = ?
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:Let a function be fn+1(x) = fn (x) + 3 . If f2(2) = 4, find the value of f6(2).
View Solution
Question for Practice Questions Level 1: Functions - 1
Try yourself:Let A = {a, b, c}. Then, the range of the relation R = {(a, b), (a, c), (b, c)} defined on A is
View Solution
Download as PDF
Related Searches

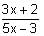
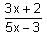
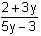
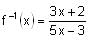
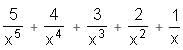 + 1 + x + 2x2 + 3x3 + 4x4 + 5x5
+ 1 + x + 2x2 + 3x3 + 4x4 + 5x5