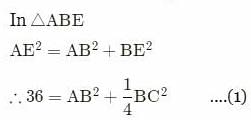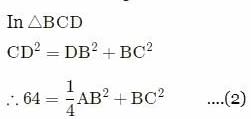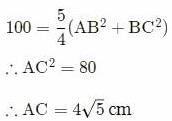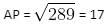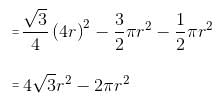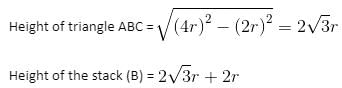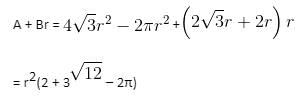This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Geometry (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Geometry - 1
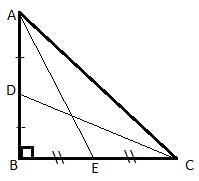
Try yourself:If the medians of a right-angled triangle, which are drawn from the vertices of the acute angles, measure 6 cm and 8 cm, find the length of the hypotenuse.
View Solution
Question for Practice Questions Level 2: Geometry - 1
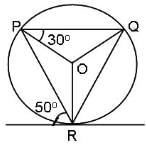
Try yourself:If O is the centre of the circle and R is the point of contact of the tangent, then what is the measure of ∠ORQ?
View Solution
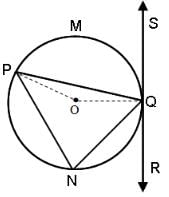
Question for Practice Questions Level 2: Geometry - 1
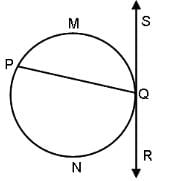
Try yourself:Find the measure of angle PQS, if the measure of arc PMQ is 150°.
View Solution
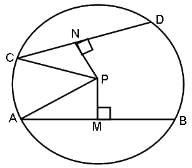
Question for Practice Questions Level 2: Geometry - 1
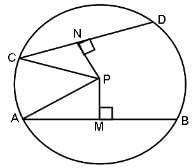
Try yourself:What is the length of PN, if AB = 30, PM = 8, DC = 16 and P is the centre of the circle?
View Solution
Question for Practice Questions Level 2: Geometry - 1
Try yourself:Four tangents to a circle form a parallelogram PQRS. Find the length of side PS.
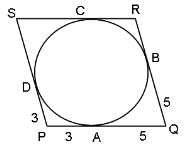
View Solution
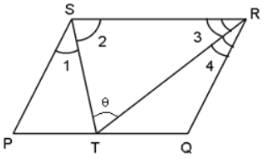
Question for Practice Questions Level 2: Geometry - 1
Try yourself:If PS || QR, ∠1 = ∠2 and ∠3 = ∠4, then what is the measure of ∠STR?
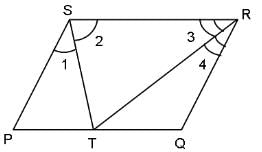
View Solution
Question for Practice Questions Level 2: Geometry - 1
Try yourself:The sum of the interior angles of a triangle is 180°. How many sides does a polygon have if the sum of its interior angles is 2520°?
View Solution
Question for Practice Questions Level 2: Geometry - 1
Try yourself:In the given figure, AB || CD. Find angle BGF.
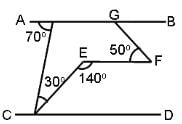
View Solution
Question for Practice Questions Level 2: Geometry - 1
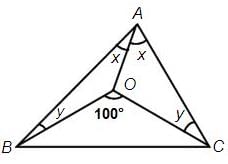
Try yourself:In the following figure, OA bisects ∠A, ∠ABO = ∠ACO and ∠BOC = 100°. Find the measure of ∠AOB.
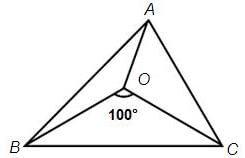
View Solution
Question for Practice Questions Level 2: Geometry - 1
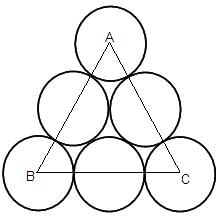
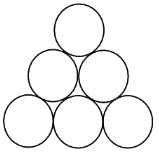
Try yourself:Six circles, each of radius r feet, are placed as shown in the figure below. If A is the area bounded by but not included in the circles (in square feet), and B is the height of the stack (in feet), then find the value of A + Br.
View Solution
Download as PDF
Related Searches