Practice Questions: Lines and Angles | Maths Olympiad Class 6 PDF Download

Q1: How many right angles form a straight angle?
Sol:
We know that a right angle measures 90°.
A straight angle measures 180°.
To find how many right angles make one straight angle:
$\mathrm{180°}÷\mathrm{90°}=2180^\backslash circ\; \backslash div\; 90^\backslash circ\; =\; 2$
So, two right angles form a straight angle.
Answer: Two right angles.

Q2: If $\backslash angle\; XYZ\; =\; 80^\backslash circ$∠XYZ=80° and $\backslash angle\; XYW\; =\; 30^\backslash circ$∠XYW=30°, and both angles share the same arm 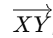, what is the angle between the non-shared arms?

Sol:
The total angle between the non-shared arms is the sum of both given angles:
80° + 30° = 110°
So, the angle between the non-shared arms is 110°.
Answer: 110°

Q3: Two angles $\backslash angle\; JKL\; =\; 50^\backslash circ$∠JKL=50° and ∠MKL=60° share a common vertex K. What is their combined angle?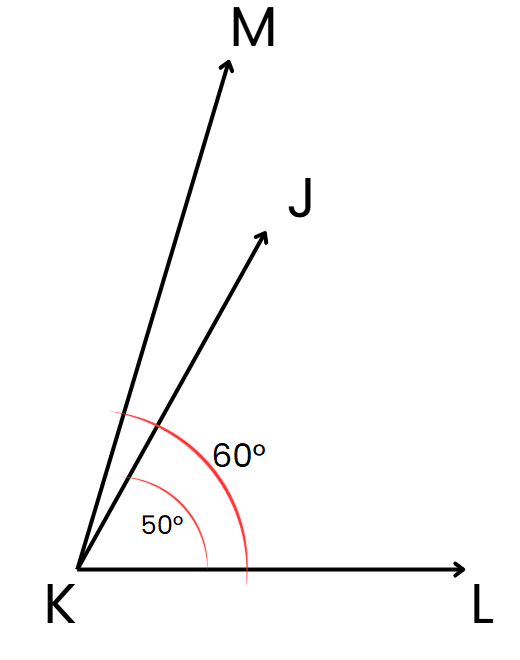
Sol:
When two angles share a common vertex and arm, we can add them to get the combined angle:
50° + 60° = 110°
So, the total angle formed is 110°.
Answer: 110°

Q4: A student measures an angle of 100° using a protractor, but the reading shows 95°. What is the misalignment angle?
Sol:
To find the misalignment, subtract the incorrect reading from the actual angle:
$100^\backslash circ\; -\; 95^\backslash circ\; =\; 5^\backslash circ$100° − 95° = 5°
So, the protractor was misaligned by 5°.
Answer: 5° misalignment

Q5: A 160° angle is bisected three times. What is the measure of the smallest angle formed after all the bisections?
Sol:
We divide the angle step by step:

• First bisection:
  $160^\backslash circ\; \backslash div\; 2\; =\; 80^\backslash circ$160° ÷ 2 = 80°

• Second bisection:
  80° ÷ 2 = 40°

• Third bisection:
  $40^\backslash circ\; \backslash div\; 2\; =\; 20^\backslash circ$40° ÷ 2 = 20°
  After three bisections, the smallest angle formed is 20°.
  Answer: 20°

Q6: A point is marked on a paper and labeled P. How many dimensions does it have?
Sol: A point only shows a position and has no length, width, or height.
Answer: A point has zero dimensions.

Q7: Is an angle measuring 170° acute, right, or obtuse?
Sol: An angle between 90° and 180° is called an obtuse angle.
Answer: Obtuse angle.

Q8: Two angles share a common vertex Q and one common arm. One measures 60°, the other 45°. What is the angle between the outer arms?
Sol: The angle between the outer arms is the sum of the angles:
60° + 45° = 105°
Answer: 105°

Q9: Compare ∠ABC=70° and $\backslash angle\; DEF\; =\; 110^\backslash circ$∠DEF=110°. Which is larger?
Sol: 110° > 70°, so ∠DEF is larger.
Answer: $\backslash angle\; DEF$∠DEF is larger.

Q10: A carpenter uses a square tool that forms a 90° angle. What is this angle called?
Sol: An angle of 90° is called a right angle.
Answer: Right angle.

Q11: Classify the angle made by the hands of a clock at 10 o’clock.
Sol: 

• At 10 o’clock, the hour hand is at 10 and the minute hand is at 12.
• The angle between each number on the clock = 360° ÷ 12 = 30°.
• From 10 to 12, there are 2 hour spaces.
• So, the angle between the hands = 2 × 30° = 60°

Answer: The angle is 60°, which is an acute angle (since it's less than 90°).

Q12: The sum of three angles on a straight line is 180°. Two angles are 2x and x. Find the third if it's double the second.
Sol:
Let angles be 2x, x, and 2x.
Sum = 2x + x + 2x = 5x = 180° 

⇒ x = 36°
Angles: 72°, 36°, 72°
Answer: 72°, 36°, 72°

Q13: A paper circle is folded into a semicircle, then into a quarter circle, and once more. What is the angle at the final fold, and how many times was the original angle divided?

Sol:
Total angle of a full circle = 360°

Step 1:
First fold → semicircle
360° ÷ 2 = 180°

Step 2:
Second fold → quarter circle
180° ÷ 2 = 90°

Step 3:
Third fold
90° ÷ 2 = 45°

So, the final angle after 3 folds = 45°

Now, total number of equal parts the original circle is divided into:
360° ÷ 45° = 8 parts

Q14: A slit with a 72° angle is cut in cardboard. Three rotating arms have angles 70°, 72°, and 74°. Which arm(s) pass through the slit, and why?

Sol:

• The slit angle is 72°.

• For an arm to pass through, its angle must be equal to or smaller than the slit (but not wider).

• The arm with 70° is narrower than the slit → it might pass through.

• The arm with 72° is exactly equal → it fits perfectly.

• The arm with 74° is wider than the slit → it will not pass.

However, usually only an arm exactly equal to the slit angle fits snugly without wobble or force.

Answer: Only the 72° arm passes through the slit, because it exactly matches the slit angle. The 70° is too narrow and the 74° is too wide.

Q15: A full turn is divided into five equal angles. What is the measure of each, and classify them.

Sol:

• A full turn = 360°

• Dividing into 5 equal angles:

$360\circ ÷5=72\circ 360^\backslash circ\; \backslash div\; 5\; =\; 72^\backslash circ$360∘÷5=72∘

• Since 72° < 90°, each angle is an acute angle.

Answer:
Each angle = 72°, and it is an acute angle.