Practice Questions: Patterns in Mathematics | Maths Olympiad Class 6 PDF Download
1. Identify the pattern for the following sequence and find the next number.
2, 3, 5, 8, 12, 17, 23, ____.
Ans:
Given,
2, 3, 5, 8, 12, 17, 23, ____
The pattern involved in the given sequence is:
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 4 = 12
12 + 5 = 17
17 + 6 = 23
23 + 7 = 30
Therefore, the next number of the given sequence is 30.
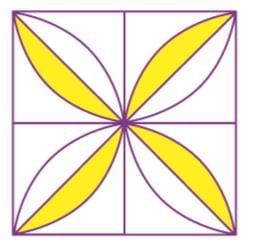
2. Observe the below figure and identify the missing part.
Ans:
Consider the question figure, where the design in each part will be obtained by rotating the previous design by 90 degrees in the clockwise direction.
So, the missing part will be option (b).
Hence, the complete figure is:
3. Write the next three numbers of the following sequence.
173, 155, 137, 119, 101
Ans:
173, 155, 137, 119, 101
The pattern in the given sequence is:
173 – 18 = 155
155 – 18 = 137
137 – 18 = 119
119 – 18 = 101
So, the next three numbers can be written as:
101 – 18 = 83
83 – 18 = 65
65 – 18 = 47
Thus, the sequence is 173, 155, 137, 119, 101, 83, 65, 47.
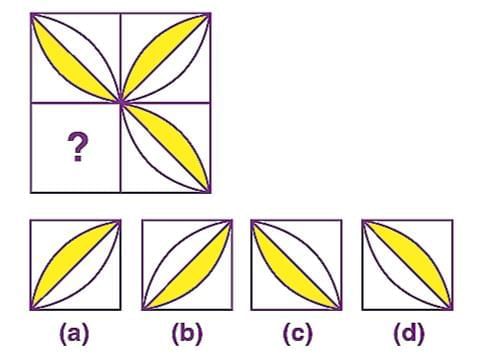
4. Observe the following figure and choose the correct option.
Ans:
Each part of the square box contains a triangle inscribed in the circle in the given figure. Also, the triangle in the next circle is the vertical image of the previous one.
Similarly, in the second row, the triangle in the missing part will be an image of the previous one.
Thus, the missing part is option (a).
5. What is the formula for the pattern for this sequence?
11, 21, 31, 41, 51, 61, 71
Ans:
Given,
11, 21, 31, 41, 51, 61, 71
The numbers in this sequence are written as:
11 + 10 = 21, 21 + 10 = 31, 31 + 10 = 41, and so on.
This can also be expressed as:
11 = 10 + 1 = 10 × 1 + 1
21 = 20 + 1 = 10 × 2 + 1
31 = 30 + 1 = 10 × 3 + 1
41 = 40 + 1 = 10 × 4 + 1 and so on.
From this, we can write the formula for the above pattern as: 10n + 1, where n = 1, 2, 3, etc.
6. Find the pattern in the sequence and write the next two numbers.
10, 17, 36, 73, 134,…
Ans:
Given sequence is:
10, 17, 36, 73, 134,…
10 = 13 + 9
17 = 23 + 9
36 = 33 + 9
73 = 43 + 9
134 = 53 + 9
So, the next number = 63 + 9 = 216 + 9 = 225
Again, the next number = 73 + 9 = 343 + 9 = 352
Therefore, the sequence is:
10, 17, 36, 73, 134, 225, 352.
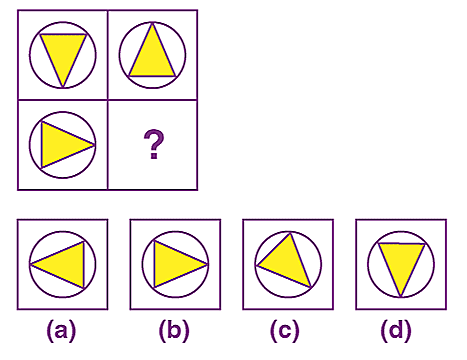
7. Observe the pattern given below. Find the missing number.
Ans:
In the given figure, we can observe that the sum of the four numbers is equal to the number written in the middle of the shape.
That means,
11 + 22 + 33 + 44 = 110
16 + 24 + 32 + 40 = 112
? + 23 + 34 + 12 = 114
? = 114 – 23 – 34 – 12 = 45
Therefore, the missing number is 45.
8. What is the next number of the following sequence?
20, 18, 21, 16, 23, 12, 25, 8, 27, 4, 33, ?
Ans:
Given sequence:
20, 18, 21, 16, 23, 12, 25, 8, 27, 4, 33
Let us find the difference between two consecutive numbers of the sequence to identify the pattern.
18 – 20 = -2
21 – 18 = 3
16 – 21 = -5
23 – 16 = 7
12 – 23 = -11
25 – 12 = 13
8 – 25 = -17
27 – 8 = 19
4 – 27 = -23
33 – 4 = 29
Here, we can see that the differences are the prime numbers.
So, the number number = 33 – 31 = 2
9. Estimate the next number of the following sequence.
1, 2, 6, 15, 31, ?
Ans:
Given,
1, 2, 6, 15, 31, ?
Let’s write the difference between consecutive numbers.
2 – 1 = 1
6 – 2 = 4
15 – 6 = 9
31 – 15 = 16
Here, 1 = 12, 4 = 22, 9 = 32, 16 = 42.
Thus, the next number of the sequence will be obtained by adding 52, i.e. 25, to the previous number.
Therefore, 31 + 52 = 31 + 25 = 56.
10. What will be the next number of the given sequence?
1, 5, 12, 22, 35, ?
Ans:
Given sequence is:
1, 5, 12, 22, 35, ?
Let’s write the difference between consecutive numbers.
5 – 1 = 4
12 – 5 = 7
22 – 12 = 10
35 – 22 = 13
The difference between these numbers follows a pattern that 3 is odd to the previous difference.
So, the next number will be obtained by adding 13 + 3, i.e. 16 to 35.
Hence, the next number = 35 + 16 = 51.
|
30 videos|120 docs|59 tests
|
FAQs on Practice Questions: Patterns in Mathematics - Maths Olympiad Class 6
| 1. What are patterns in mathematics, and why are they important for Class 6 students? |  |
| 2. How can students identify patterns in numbers and shapes? |  |
| 3. What are some examples of patterns that students might encounter in Class 6 mathematics? |  |
| 4. How do patterns relate to algebra in Class 6 math? |  |
| 5. What activities can teachers use to teach patterns in mathematics effectively? |  |