Class 7 Maths Chapter 9 Practice Question Answers - Perimeter and Area
Q1. The area of a circle is the measurement of the region enclosed by its
(a) Radius
(b) Centre
(c) Circumference
(d) Area
Ans: (c)
Sol: As shown in the above figure, area is the region enclosed inside the boundary/circumference of the circle.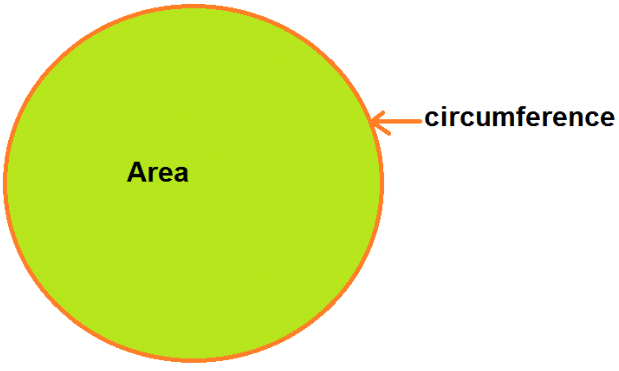
Q2. Circumference of a circle is ______
(a) πr
(b) 2πr
(c) 3πr
(d) 4πr
Ans: (b)
Sol: Circumference of a circle whose radius is r is given by 2πr.
Q3. Area of a circle is _______
(a) πr2
(b) 2π
(c) 2πr2
(d) 4πr
Ans: (a)
Sol: Area covered within the boundary of circle = π×r2 , where r is a radius of a circle.
Q4. A path of width 8 m runs around a circular park whose radius is 38 m. Find the area of the path.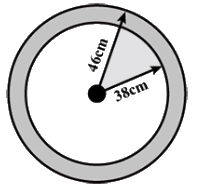 (a) 2112 m2
(a) 2112 m2
(b) 2834 m2
(c) 3212 m2
(d) 1578 m2
Ans: (a)
Sol: Inner radius (Radius of the park) =38 m
Outer radius (Radius of the park + path width of the park) =38+8=46 m
Area of the path =π(462 −382 )
= 22/7 (2116−1444)
= 22/7 (672)
=2112 m2
Q5. The circumference of a circular field is 308m. Find its radius in metres.
(a) 49m
(b) 59m
(c) 91m
(d) 94m
Ans: (a)
Sol: The circumference of a circular field is 308m
Therefore, 2πr=308
⇒ r = 308 x 7 / 2 x 22
⇒ r = 49 m
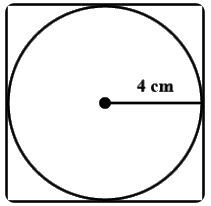
Q6. A circle is inscribed in a square as shown below. If the radius of the circle is 4 cm, then the perimeter of the square is ______
 (a) 28 cm
(a) 28 cm
(b) 24 cm
(c) 32 cm
(d) 36 cm
Ans: (c)
Sol: From the fig it is clear that,
Diameter of the circle = side of the square
So length of side of square = 2 × 4 cm
=8 cm
∴ perimeter of the square = 8 + 8 + 8 + 8
=32 cm
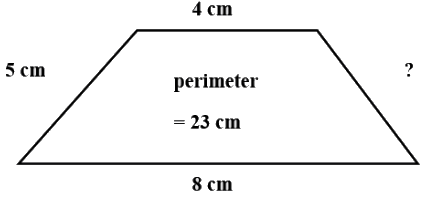
Q7. Find the missing length of the following figure.
 (a) 6 cm
(a) 6 cm
(b) 4 cm
(c) 2 cm
(d) 5 cm
Ans: (a)
Sol: Let unknown side of the figure is x
Perimeter = sum of all sides of figure
23 = 4 + 5 + 8 + x
x = 23 − 17 = 6 cm.
Q8. Find the missing length of the figure given below.
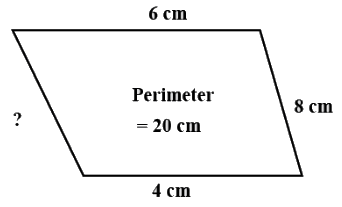 (a) 4 cm
(a) 4 cm
(b) 2 cm
(c) 6 cm
(d) 8 cm
Ans: (b)
Sol: Let unknown side is x
Perimeter = sum of length.
20 = 6 + 4 + 8 + x
x = 20 − 18 = 2 cm
Q9. If the radii of two concentric circles are 15 cm and 13 cm, respectively, then the area of the circulating ring in sq. cm will be:
(a) 176
(b) 178
(c) 180
(d) 200
Ans: (a)
Sol: R=15 cm,r=13 cm.
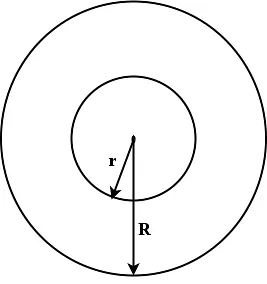 Area of the circulating ring = π(R2 - r2)
Area of the circulating ring = π(R2 - r2)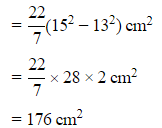
Q10. Perimeter of a triangle is the sum of the lengths of all the _____ sides.
(a) 4
(b) 2
(c) 3
(d) 6
Ans: (c)
Sol: Perimeter of a triangle is the sum of the lengths of all the three sides.
Q11. The radius of a wheel is 0.25m. How many rounds will it take to complete the distance of 11km?
(a) 7000
(b) 8000
(c) 9000
(d) 6000
Ans: (a)
Sol: Distance covered in one round = Circumference of wheel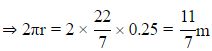
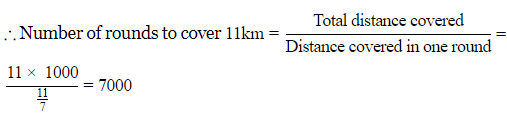
Q12. The area of a triangle with base 10 cm and height 8 cm is:
(a) 18 cm²
(b) 40 cm²
(c) 80 cm²
(d) 32 cm²
Ans: (b)
Sol: Area of a triangle = (1/2) × base × height
= (1/2) × 10 cm × 8 cm
= 40 cm².
Q13. The perimeter of an equilateral triangle is 30 cm. What is the length of each side?
(a) 10 cm
(b) 15 cm
(c) 12 cm
(d) 8 cm
Ans: (a)
Sol: Perimeter of an equilateral triangle = 3 × side length.
30 cm = 3 × side length.
Side length = 30 cm / 3 = 10 cm.
Q14. The area of a parallelogram with base 12 cm and height 8 cm is:
(a) 80 cm²
(b) 96 cm²
(c) 40 cm²
(d) 24 cm²
Ans: (b)
Sol: Area of a parallelogram = base × height
= 12 cm × 8 cm
= 96 cm².
Q15. A circular garden has a radius of 7 meters. What is the area of the garden in square meters? (Use π = 22/7)
(a) 154 m²
(b) 154 cm²
(c) 1540 m²
(d) 1540 cm²
Ans: (a)
Sol: Area of a circle = π × radius²
= (22/7) × 7 m × 7 m
= 154 m².
|
77 videos|386 docs|39 tests
|
FAQs on Class 7 Maths Chapter 9 Practice Question Answers - Perimeter and Area
| 1. What is the formula to calculate the perimeter of a rectangle? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. How can I calculate the area of a circle? |  |
| 5. Is there a specific formula for the perimeter of a polygon? |  |
















