Class 8 Maths Chapter 9 Practice Question Answers - Mensuration
Q1: In a trapezium, the parallel sides measure 40 cm and 20 cm. Calculate the area of the trapezium if its non-parallel sides are equal having the lengths of 26 cm.
Sol:
From the question statement draw the diagram.
Consider a trapezium of ABCD. Let AB and DC be the parallel sides as shown in the figure.
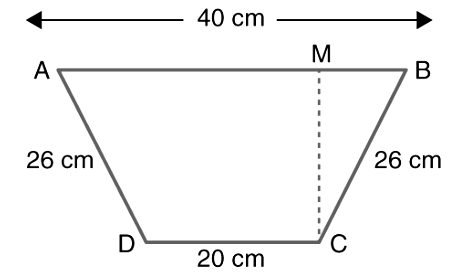
Now, CM will be the distance between the two parallel sides or the height of the trapezium.
We know,
Area of trapezium = ½ × sum of parallel sides × height.
So, height has to be found.
In the diagram, draw CL || AD
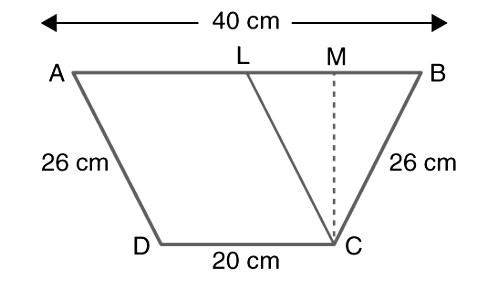
Now, ALCD is a parallelogram ⇒ AL = CD = 20 cm and CL = AD = 26 cm
As AD = CB,
CL = CB ⇒ ΔCLB is an isosceles triangle with CB as its height.
Here, BL = AB – AL = (40 – 20) = 20 cm. So,
LM = MB = ½ BL = ½ × 20 = 10 cm
Now, in ΔCLM,
CL2 = CM2 + LM2 (Pythagoras Theorem)
262 = CM2 + 102
CM2 = 262 – 102
Using algebraic identities, we get; 262 – 102 = (26 – 10) (26 + 10)
hence,
CM2 = (26 – 10) (26 + 10) = 16 × 36 = 576
CM = √576 = 24 cm
Now, the area of trapezium can be calculated.
Area of trapezium, ABCD = ½ × (AB + CD) × CM
= ½ × (20 + 40) × 24
Or, Area of trapezium ABCD = 720 cm2
Q2: From a circular sheet of radius 4 cm, a circle of radius 3 cm is cut out. Calculate the area of the remaining sheet after the smaller circle is removed.
Sol:
The area of the remaining sheet after the smaller circle is removed will be = Area of the entire circle with radius 4 cm – Area of the circle with radius 3 cm
We know,
Area of circle = πr²
So,
Area of the entire circle = π(4)² = 16π cm2
And,
Area of the circle with radius 3 cm which is cut out = π(3)² = 9π cm2
Thus, the remaining area = 16π – 9π = 7π cm2
Q3: A lawnmower takes 750 complete revolutions to cut grass on a field. Calculate the area of the field if the diameter of the lawnmower is 84 cm and the length is 1 m.
Sol:
Given, length of lawnmower = 1m = 100cm
Its circumference = π × D = 22/7 × 84 = 264 cm
Length of field will be = 264 × 750 = 198000 cm
Here, the width of field = length of the lawnmower i.e. 100 cm
So, area of field = 198000 × 100 = 19,800,000 cm²
Or, 1980 m²
Q4: Calculate the height of a cuboid which has a base area of 180 cm2 and volume is 900 cm3.
Sol:
Volume of cuboid = base area × height
900 = 180 × height
So, height = 900/180
= 5 cm
Q5: The parallel sides of a trapezium measure 12 cm and 20 cm. Calculate its area if the distance between the parallel lines is 15 cm.
Sol:
Area of trapezium = ½ × perpendicular distance between parallel sides × sum of parallel sides
= ½ × 15 × (12 + 20)
= 1/2 × 15 × 32
= 15 × 16
= 240 cm2
Q6: A square and a rectangle have the same perimeter. Calculate the area of the rectangle if the side of the square is 60 cm and the length of the rectangle is 80 cm.
Sol:
Perimeter of square formula = 4 × side of the square
Hence, P (square) = 4 × 60 = 240 cm
Perimeter of rectangle formula = 2 × (Length + Breadth)
Hence, P (rectangle) = 2 (80 + Breadth)
= 160 + 2 × Breadth
According to the given question,
160 + 2 × Breadth = 240 cm
2 × Breadth = 240 – 160
Breadth = 80/2
The breadth of the rectangle = 40 cm
Now, the area of rectangle = Length × Breadth = 80 × 40 = 3200 cm2
Q7: The area of a rhombus is 16 cm2 and the length of one of its diagonal is 4 cm. Calculate the length of other diagonal.
Sol:
Area of rhombus = ½ × d1 × d2
⇒ 16 = ½ × 4 × d2
So, d2 = 32/4
= 8 cm
Q8: A cuboidal box of dimensions 1 m × 2 m × 1.5 m is to be painted except its bottom. Calculate how much area of the box has to be painted.
Sol:
Given,
Length of the box, l = 2 m,
Breadth of box, b = 1 m
Height of box, h = 1.5 m
We know that the surface area of a cuboid = 2(lb + lh + bh)
But here the bottom part is not to be painted.
So,
Surface area of box to be painted = lb + 2(bh + hl)
= 2 × 1 + 2 (1 × 1.5 + 1.5 × 2)
= 2 + 2 (1.5 + 3.0)
= 2 + 9.0
= 11
Hence, the required surface area of the cuboidal box = 11 m2
Q9: A flooring tile is in the shape of a parallelogram with 24 cm base and the corresponding 10 cm height. Calculate the number of tiles required to cover a floor of area 1080 m2 (If required you can split the tiles in whatever way you want to fill up the corners).
Sol: The area of a parallelogram is given by the formula: Area = base × height.
Given the base = 24 cm and height = 10 cm, the area of one tile is:
Area of one tile = 24 cm × 10 cm = 240 cm²
Now, we need to convert the area of the floor from square meters to square centimeters since the area of the tile is in square centimeters.
1 m² = 10000 cm²
So, the area of the floor = 1080 m² × 10000 cm²/m² = 10800000 cm²
Now, to find the number of tiles required, divide the total area of the floor by the area of one tile:
Number of tiles required = Total floor area / Area of one tile
Number of tiles required = 10800000 cm² / 240 cm² = 45000
So, 45000 tiles are required to cover the floor.
Q10: How many bricks each 25 cm by 15 cm by 8 cm, are required for a wall 32 m long, 3 m high and 40 cm thick?
Sol: First, let's calculate the volume of one brick:
Volume of one brick = Length × Width × Height
Volume of one brick = 25 cm × 15 cm × 8 cm = 3000 cm³
Now, let's calculate the volume of the wall:
Volume of the wall = Length × Width × Height
Volume of the wall = 3200 cm × 300 cm × 40 cm = 38400000 cm³
Now, we'll find out how many bricks are required to build the wall by dividing the total volume of the wall by the volume of one brick:
Number of bricks required = Total wall volume / Volume of one brick
Number of bricks required = 38400000 cm³ / 3000 cm³ = 12800
So, 12800 bricks, each measuring 25 cm by 15 cm by 8 cm, are required to build the wall.
Q11: Two cubes are joined end to end. Now, calculate the volume of the resulting cuboid, if each side of the cubes is 6 cm.
Sol: When two cubes are joined end to end, they form a cuboid. The length of the resulting cuboid will be equal to the combined length of the two cubes, the width will be equal to the side of the cubes, and the height will be equal to the side of the cubes.
Given that each side of the cubes is 6 cm:
Length of the resulting cuboid = 6 cm + 6 cm = 12 cm
Width of the resulting cuboid = 6 cm
Height of the resulting cuboid = 6 cm
The volume of a cuboid is given by the formula:
Volume = Length × Width × Height
Substitute the values:
Volume = 12 cm × 6 cm × 6 cm = 432 cm³
So, the volume of the resulting cuboid is 432 cubic centimeters.
Q12: Find the area of a rhombus whose one side measures 5 cm and one diagonal as 8 cm.
Sol: The area of a rhombus can be calculated using the formula:
Area = (diagonal1 × diagonal2) / 2
Given that one diagonal is 8 cm and the side length is 5 cm, we can use the properties of a rhombus to find the other diagonal.
In a rhombus, the diagonals are perpendicular bisectors of each other, meaning they intersect at a right angle and divide each other into two equal parts.
Using the Pythagorean theorem, we can find the length of the other half of the diagonal (let's call it d):
d² + (5/2)² = 8²
d² + 25/4 = 64
d² = 64 - 25/4
d² = 256/4 - 25/4
d² = 231/4
d = √(231/4)
d = √231 / 2
Now that we have both diagonals, we can calculate the area:
Area = (8 cm × (√231 / 2 cm)) / 2
Area = (4√231) cm²
So, the area of the rhombus is 4√231 square centimeters.
|
81 videos|423 docs|31 tests
|
















