Q1: Consider the complex function 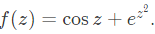 The coefficient of z5 in the Taylor series expansion of f(z) about the origin is _____ (rounded off to 1 decimal place). (2024)
The coefficient of z5 in the Taylor series expansion of f(z) about the origin is _____ (rounded off to 1 decimal place). (2024)
(a) 0
(b) 0.5
(c) 0.8
(d) 0.2
Ans: (a)
Sol: 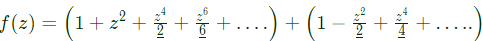 It is series is of even powers.
It is series is of even powers.
∴ Coefficient of z5 = 0.
Q2: Which of the following complex functions is/are analytic on the complex plane? (2024)
(a) f(z) = jRe(z)
(b) f(z) = Im(z)
(c) f(z) = e∣z∣
(d) f(z) = z2−z
Ans: (d)
Sol: Let us take (a), f(z) = z2−z
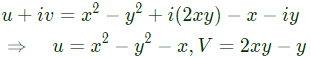 Now by C−R equation,
Now by C−R equation,
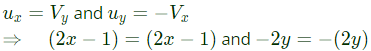 i.e. C-R equation are satisfied.
i.e. C-R equation are satisfied.
Q3: Let R be a region in the first quadrant of the xy plane enclosed by a closed curve C considered in counter-clockwise direction. Which of the following expressions does not represent the area of the region R? (2022)
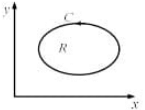 (a)
(a) 
(b) 
(c) 
(d) 
Ans: (c)
Sol: Using green theorem?s
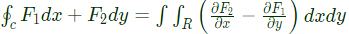 Check all the options:
Check all the options:
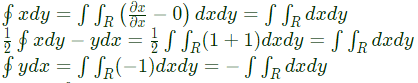 Hence,
Hence, 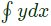 is not represent the area of the region.
is not represent the area of the region.
Q4: Let 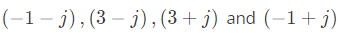 be the vertices of a rectangle C in the complex plane. Assuming that C is traversed in counter-clockwise direction, the value of the contour integral
be the vertices of a rectangle C in the complex plane. Assuming that C is traversed in counter-clockwise direction, the value of the contour integral  (2021)
(2021)
(a) jπ/2
(b) 0
(c) -jπ/2
(d) jπ/16
Ans: (c)
Sol: 
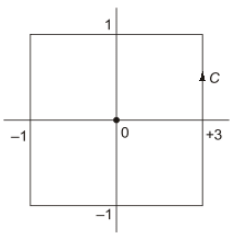 Singularities are given by z2(z−4) = 0
Singularities are given by z2(z−4) = 0
⇒ z = 0, 4
z = 0 is pole of order m = 2 lies inside contour 'c'
z = 4 is pole of order m = 1 lies outside 'c'
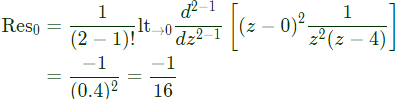 By CRT
By CRT

Q5: Let p(z) = z3 + (1 + j)z2 + (2 + j)z + 3, where z is a complex number.
Which one of the following is true? (2021)
(a) conjugate {p(z)} = p(conjugate {z}) for all z
(b) The sum of the roots of p(z) = 0 is a real number
(c) The complex roots of the equation p(z) = 0 come in conjugate pairs
(d) All the roots cannot be real
Ans: (d)
Sol: Since sum of the roots is a complex number
⇒ absent one root is complex
So all the roots cannot be real.
Q6: The real numbers, x and y with y = 3x2 + 3x + 1, the maximum and minimum value of y for x ∈ [−2, 0] are respectively ________ (2020)
(a) 7 and 1/4
(b) 7 and 1
(c) -2 and -1/2
(d) 1 and 1/4
Ans: (a)
Sol: 
 Maximum value of y in [-2, 0] is maximum {f(-2), f(0)}
Maximum value of y in [-2, 0] is maximum {f(-2), f(0)}
max{7, 1} = 7
Minimum value of y in [-2, 0]
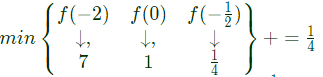 Maximum value 7, minimum value 1/4.
Maximum value 7, minimum value 1/4.
Q7: The value of the following complex integral, with C representing the unit circle centered at origin in the counterclockwise sense, is: (2020)
 (a) 8πi
(a) 8πi
(b) -8πi
(c) -πi
(d) πi
Ans: (c)
Sol: 
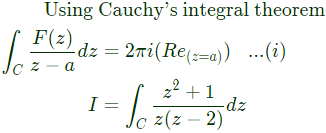 Poles are at z = 0 and 2 but only z = 0 lies inside the unit circle.
Poles are at z = 0 and 2 but only z = 0 lies inside the unit circle.
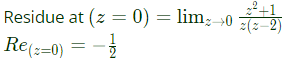 Using equation (i)
Using equation (i)

Q8: Which of the following is true for all possible non-zero choices of integers m, n; m ≠ n, or all possible non-zero choices of real numbers p, q; p ≠ q, as applicable? (2020)
(a) 
(b) 
(c) 
(d) 
Ans: (c)
Sol: 
Q9: ax3 + bx2 + cx + d is a polynomial on real x over real coefficients a, b, c, d wherein a ≠ 0. Which of the following statements is true? (2020)
(a) d can be chosen to ensure that x = 0 is a root for any given set a, b, c.
(b) No choice of coefficients can make all roots identical.
(c) a, b, c, d can be chosen to ensure that all roots are complex.
(d) c alone cannot ensure that all roots are real.
Ans: (a, d)
Sol: Given Polynomial 
Option (A):
If d = 0, then the polynomial equation becomes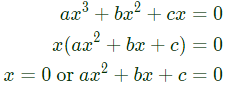 d can be choosen to ensure x = 0 is a root of given polynomial.
d can be choosen to ensure x = 0 is a root of given polynomial.
Hence, Option (A) is correct.
Option B:
A third degree polynomial equation with all root equal is given by
(x+α)3 = 0
Thus, by selecting suitable values of a, b, c and d we can have all roots identical.
Hence, option (B) is incorrect.
Option (C): Complex roots always occurs in pairs,
So, the given polynomial will have maximum of 2 complex roots and 1 real root.
Hence, option (C) is incorrect.
Option (D): Nature or roots depends on other coefficients also apart from coefficient 'c'.
Hence, option (D) is correct.
Hence, the correct options are (A) and (D).
Q10: The closed loop line integral 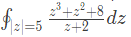 evaluated counter-clockwise, is (2019)
evaluated counter-clockwise, is (2019)
(a) +8jπ
(b) -8jπ
(c) -4jπ
(d) +4jπ
Ans: (a)
Sol: 

Q11: Which one of the following functions is analytic in the region |z∣ ≤ 1? (2019)
(a) 
(b) 
(c) 
(d) 
Ans: (b)
Sol: 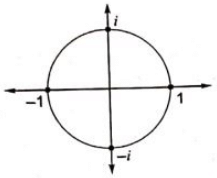 By Cauchy integral theorem,
By Cauchy integral theorem,
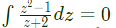 Therefore,
Therefore, 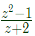 is analytic in the region ∣z∣ ≤ 1.
is analytic in the region ∣z∣ ≤ 1.
Q12: If C is a circle |z| = 4 and  (2018)
(2018)
(a) 1
(b) 0
(c) -1
(d) -2
Ans: (b)
Sol: 




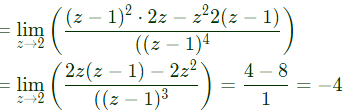 By residue theorem,
By residue theorem, 
Q13: The value of the integral 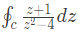 in counter clockwise direction around a circle C of radius 1 with center at the point z = -2 is (2018)
in counter clockwise direction around a circle C of radius 1 with center at the point z = -2 is (2018)
(a) πi/2
(b) 2πi
(c) -(πi/2)
(d) -2πi
Ans: (a)
Sol: 

Q14: The value of the contour integral in the complex-plane 
Along the contour |Z| = 3, taken counter-clockwise is (SET-2 (2017))
(a) -18πi
(b) 0
(c) 14πi
(d) 48πi
Ans: (c)
Sol: Pole, z = 2 lies inside |z| = 3
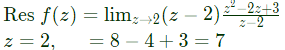 By Cauche redisue theorem,
By Cauche redisue theorem,
I = 2πi(7) = 14πi
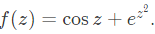 The coefficient of z5 in the Taylor series expansion of f(z) about the origin is _____ (rounded off to 1 decimal place). (2024)
The coefficient of z5 in the Taylor series expansion of f(z) about the origin is _____ (rounded off to 1 decimal place). (2024)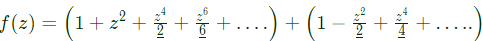 It is series is of even powers.
It is series is of even powers.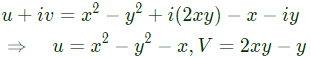 Now by C−R equation,
Now by C−R equation,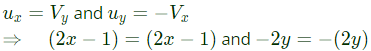 i.e. C-R equation are satisfied.
i.e. C-R equation are satisfied. (a)
(a) 



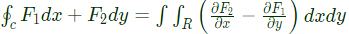 Check all the options:
Check all the options: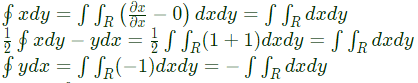 Hence,
Hence, 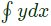 is not represent the area of the region.
is not represent the area of the region.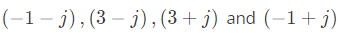 be the vertices of a rectangle C in the complex plane. Assuming that C is traversed in counter-clockwise direction, the value of the contour integral
be the vertices of a rectangle C in the complex plane. Assuming that C is traversed in counter-clockwise direction, the value of the contour integral  (2021)
(2021)
 Singularities are given by z2(z−4) = 0
Singularities are given by z2(z−4) = 0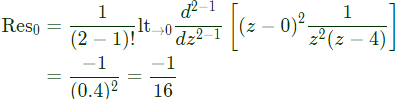 By CRT
By CRT

 Maximum value of y in [-2, 0] is maximum {f(-2), f(0)}
Maximum value of y in [-2, 0] is maximum {f(-2), f(0)}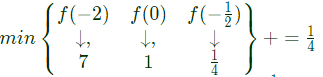 Maximum value 7, minimum value 1/4.
Maximum value 7, minimum value 1/4. (a) 8πi
(a) 8πi
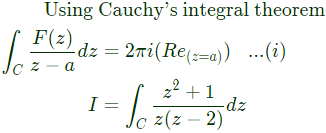 Poles are at z = 0 and 2 but only z = 0 lies inside the unit circle.
Poles are at z = 0 and 2 but only z = 0 lies inside the unit circle.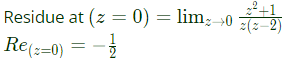 Using equation (i)
Using equation (i)






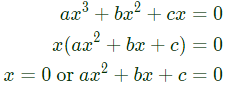 d can be choosen to ensure x = 0 is a root of given polynomial.
d can be choosen to ensure x = 0 is a root of given polynomial.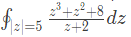 evaluated counter-clockwise, is (2019)
evaluated counter-clockwise, is (2019)





 By Cauchy integral theorem,
By Cauchy integral theorem,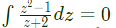 Therefore,
Therefore, 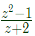 is analytic in the region ∣z∣ ≤ 1.
is analytic in the region ∣z∣ ≤ 1. (2018)
(2018)




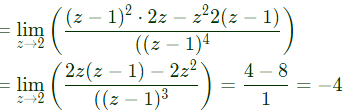 By residue theorem,
By residue theorem, 
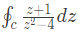 in counter clockwise direction around a circle C of radius 1 with center at the point z = -2 is (2018)
in counter clockwise direction around a circle C of radius 1 with center at the point z = -2 is (2018)


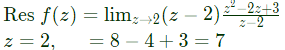 By Cauche redisue theorem,
By Cauche redisue theorem,

























