Q26: A system matrix is given as follows
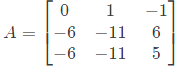 The absolute value of the ratio of the maximum eigenvalue to the minimum eigenvalue is _______. (SET-1 (2014))
The absolute value of the ratio of the maximum eigenvalue to the minimum eigenvalue is _______. (SET-1 (2014))
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c)
Sol: Characteristic equation ∣A−λI∣= 0
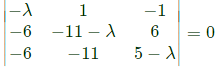
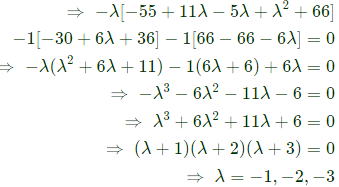 The absolute values of λ are ∣𝜆∣ = 1, 2, 3
The absolute values of λ are ∣𝜆∣ = 1, 2, 3
Ratio of maximum and minimum eigen value is = 3 : 1 = 3/1 = 3
Q27: Given a system of equations
x + 2y + 2z = b1
5x + y + 3z = b2
What of the following is true regarding its solutions (SET-1(2014))
(a) The system has a unique solution for any given b1 and b2
(b) The system will have infinitely many solutions for any given b1 and b2
(c) Whether or not a solution exists depends on the given b1 and b2
(d) The systems would have no solution for any values of b1 and b2
Ans: (b)
Q28: A Matrix has eigenvalues -1 and -2. The corresponding eigenvectors are 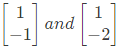 respectively. The matrix is (2013)
respectively. The matrix is (2013)
(a) 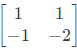
(b) 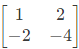
(c) 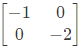
(d)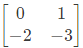
Ans: d
Sol: AX = λX
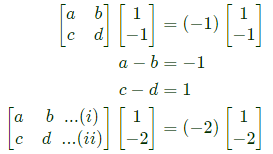
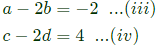 From equation (i) and (iii), a = 0 and b = 1
From equation (i) and (iii), a = 0 and b = 1
From equation (ii) and (iv), c = -2 and d = -3
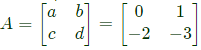
Q29: The equation 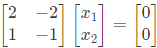 has (2013)
has (2013)
(a) no solution
(b) only one solution 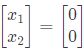
(c) non-zero unique solution
(d) multiple solutions
Ans: (d)
Sol: 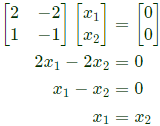 i.e. x1 and x2 are having infinite number of solutions.
i.e. x1 and x2 are having infinite number of solutions.
⇒ Multiple solutions are these.
Q30: Given that 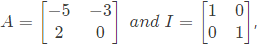 the value of A3 is (2012 )
the value of A3 is (2012 )
(a) 15A + 12I
(b) 19A + 30I
(c) 17A + 15I
(d) 17A + 21I
Ans: (b)
Sol:  Characteristic equation of A is
Characteristic equation of A is
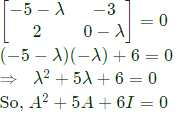 (by Cayley Hamilton theorem)
(by Cayley Hamilton theorem)
⇒ A2 = −5A − 6I
Multiplying by A on both sides, we have,
A3= −5A2 − 6A
⇒ A3 =−5(−5A−6I)−6A = 19A + 30I
Q31: The matrix 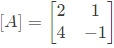 is decomposed into a product of a lower triangular matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and [U] matrices respectively are (2011)
is decomposed into a product of a lower triangular matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and [U] matrices respectively are (2011)
(a) 
(b)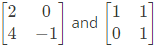
(c)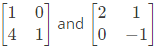
(d)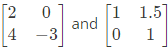
Ans: (d)
Sol: Let us try Dolittle's decomposition by putting 𝑙11 = 1 and 𝑙22 = 1
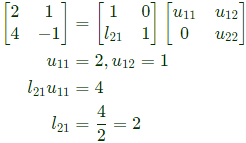
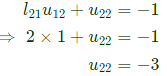 So one possible breakdown is
So one possible breakdown is
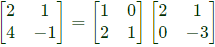 But this is not any of the choises given.
But this is not any of the choises given.
So let us do Crout's decomposition, by putting u11 = 1 and u22 = 1
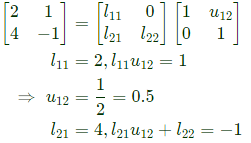
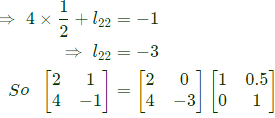
Q32: For the set of equations, x1 + 2x2 + x3 + 4x4 = 2 and 3𝑥1 + 6𝑥2 + 3𝑥3 + 12𝑥4 = 6. The following statement is true. (2010)
(a) Only the trivial solution 𝑥1 = 𝑥2 = 𝑥3 = 𝑥4 = 0 exists
(b) There are no solutions
(c) A unique non-trivial solution exists
(d) Multiple non-trivial solutions exist
Ans: (d)
Sol:  The augmental matrix is
The augmental matrix is 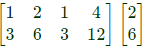
Performing gauss-elimination on this we get
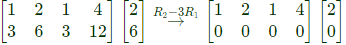 rank(A) = rank(A∣B) = 1
rank(A) = rank(A∣B) = 1
So, system is consistent.
Since, system's rank = 1 is less than the number of variables, only infinite (multiple) non-trival solution exists.
Q33: An eigenvector of 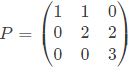 is (2010)
is (2010)
(a) 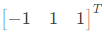
(b)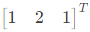
(c)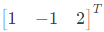
(d)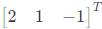
Ans: (b)
Sol: Given,
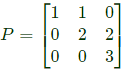
P is triangular. So eigen values are the diagonal elements themselves. Eigen values are therefore, λ1 = 1, λ2 = 2, λ3 = 3.
Now, the eigen value problem is [A − λI] 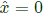
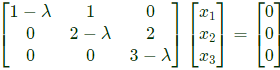 Putting λ1 = 1, we get the eigen vector corresponding to this eigen value,
Putting λ1 = 1, we get the eigen vector corresponding to this eigen value,
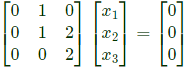 Which gives the equations
Which gives the equations
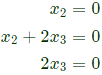 The solution is 𝑥2 = 0, 𝑥3 = 0, 𝑥1= 𝑘
The solution is 𝑥2 = 0, 𝑥3 = 0, 𝑥1= 𝑘
So, one eigen vector is 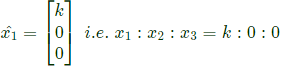
Since, none of the eigen vectors given in choises matches with this, ratio we need to proceed further and find the other eigen vectors corresponding to the other eigen values.
Now, corresponding to λ2 = 2, we get by substituting λ = 2, in the eigen value problem, the following set of equations,
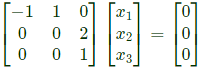 Which gives the equations,
Which gives the equations,
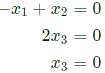 Solution is x3 = 0, x1 = k, x2 = k
Solution is x3 = 0, x1 = k, x2 = k
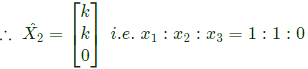 Since none of the eigen vectors given in the choises is of this ratio, we need to proceed further and find 3rd eigen vector also.
Since none of the eigen vectors given in the choises is of this ratio, we need to proceed further and find 3rd eigen vector also.
By putting λ = 3, in the eigen value problem, we get
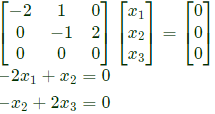
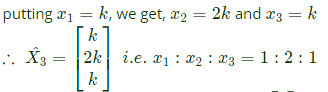 Only the eigen vector geven in choise
Only the eigen vector geven in choise 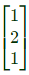 is in this ratio.
is in this ratio.
Q34: The trace and determinant of a 2 x 2 matrix are known to be -2 and -35 respectively. Its eigenvalues are (2009)
(a) -30 and -5
(b) -37 and -1
(c) -7 and 5
(d) 17.5 and -2
Ans: (c)
Sol: Trace = Sum of principal diagonal element.
Q35: Let P be a 2x2 real orthogonal matrix and  is a real vector
is a real vector  Then, which one of the following statements is correct? (2008)
Then, which one of the following statements is correct? (2008)
(a) 
(b) 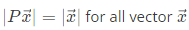
(c) 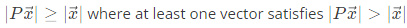
(d) No relationship can be established between 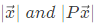
Ans: (b)
Sol: Let on orthogonal matrix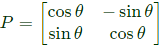 Properly of orthogonal matrix A
Properly of orthogonal matrix A
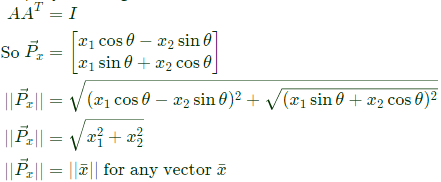
Q36: A is m × n full rank matrix with m > n and I is identity matrix. Let matrix A+ = (ATA)−1AT. Then, which one of the following statement is FALSE ? (2008)
(a) AA+A = A
(b) (AA+)2 = AA+
(c) A+A = I
(d) AA + A = A +
Ans: (b)
Sol: Choice (A) AA+A = A is corect
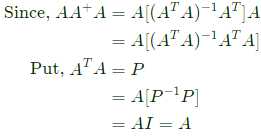
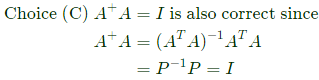
Q37: If the rank of a (5 x 6) matrix Q is 4, then which one of the following statement is correct ? (2008)
(a) Q will have four linearly independent rows and four linearly independent columns
(b) Q will have four linearly independent rows and five linearly independent columns
(c) QQT will be invertible
(d) QTQ will be invertible
Ans: (a)
Sol: If rank of (5 x 6) matrix is 4, then surely it must have exactly 4 linearly independent rows as will as 4 linearly independent columns.
Q38: The characteristic equation of a (3x3) matrix P is defined as
a(λ)∣λI−P∣ = λ3+λ2+2λ+1 = 0
If I denotes identity matrix, then the inverse of matrix P will be (2008)
(a) (P2+P+2I)
(b) (P2+P+I)
(c) −(P2+P+I)
(d) −(P2+P+2I)
Ans: (d)
Sol: If characteristic equation is
λ3 + λ2 + 2λ + 1 = 0
Then by cayley- hamilton theorem,
P3 + P2 + 2P + I = 0
I = −P3 − P2 − 2P
Multiplying by P−1 on both sides,
𝑃−1 = −𝑃2 − 𝑃 − 2𝐼 = −(𝑃2 + 𝑃 + 2𝐼)
Q39: Cayley-Hamilton Theorem states that a square matrix satisfies its own characteristic equation. Consider a matrix 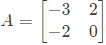 A9 equals (2007)
A9 equals (2007)
(a) 511A + 510I
(b) 309A + 104I
(c) 154A + 155I
(d) exp(9A)
Ans: a
Sol: To calculate A9
start from A2 + 3A + 2I = 0 which has been derived above
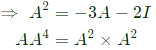

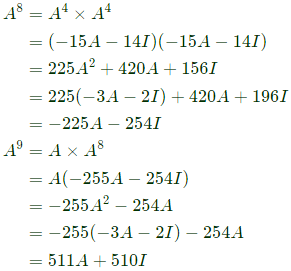
Q40: Cayley-Hamilton Theorem states that a square matrix satisfies its own characteristic equation. Consider a matrix 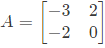 A satisfies the relation (2007)
A satisfies the relation (2007)
(a) A + 3I + 2A−1 = 0
(b) A2 + 2A + 2I = 0
(c) (A + I)(A + 2I)
(d) exp(A) = 0
Ans: (a)
Sol: 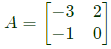
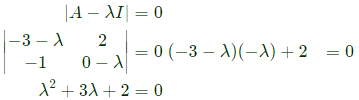 A will satisfy this equation according to cayley hamition theorem
A will satisfy this equation according to cayley hamition theorem
i.e. A2 + 3A + 2I = 0
multiplying by A−1 on both sides we get
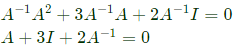
Q41: The linear operation L(x) is defined by the cross product 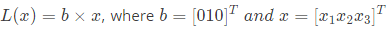 are three dimensional vectors. The 3 x 3 matrix M of this operations satisfies
are three dimensional vectors. The 3 x 3 matrix M of this operations satisfies
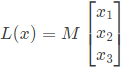 Then the eigenvalues of M are (2007)
Then the eigenvalues of M are (2007)
(a) 0, +1, -1
(b) 1, -1, 1
(c) i, -i, 1
(d) i, -i, 0
Ans: (c)
Sol: The eigen values of M are (i, −i, 1)
Q42: Let x and y be two vectors in a 3 dimensional space and <x, y> denote their dot product. Then the determinant (2007)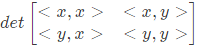 (a) is zero when x and y are linearly independent
(a) is zero when x and y are linearly independent
(b) is positive when x and y are linearly independent
(c) is non-zero for all non-zero x and y
(d) is zero only when either x or y is zero
Ans: (b)
Q43: x = [x1 x2 ... xn]T is an n-tuple nonzero vector. The nxn matrix V = xxT (2007)
(a) has rank zero
(b) has rank 1
(c) is orthogonal
(d) has rank n
Ans: (b)
Sol: The nxn matrix, V = XXT has rank 1.
Q44: If 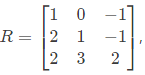 then top row of R−1 is (2005)
then top row of R−1 is (2005)
(a) [5 6 4]
(b) [5 -3 1]
(c) [2 0 -1]
(d) [2 1 1/2]
Ans: (b)
Sol:
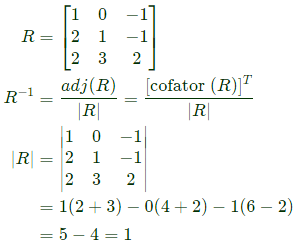 Since we need only the top row of R−1, we need to find only first column of (R) which after transpose will become first row of Adj(A).
Since we need only the top row of R−1, we need to find only first column of (R) which after transpose will become first row of Adj(A).
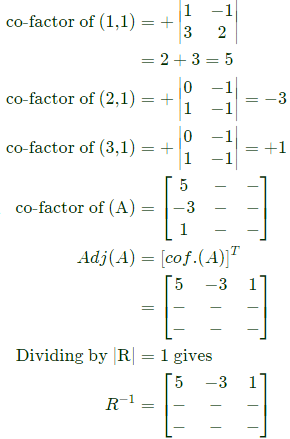
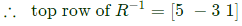
Q45: For the matrix 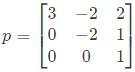 one of the eigen values is equal to -2. Which of the following is an eigen vector ? (2005)
one of the eigen values is equal to -2. Which of the following is an eigen vector ? (2005)
(a) 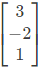
(b)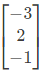
(c)
(d) 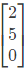
Ans: (d)
Sol: Since matrix is triangular, the eigen values are the diagonal elements themselves namely λ = 3,−2 and 1.
Corresponding to eigen value λ = −2 let us find the eigen vector
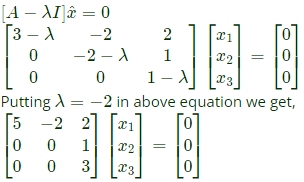 Which gives the equations,
Which gives the equations,
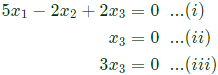 Since equation (ii) and (iii) are same we have
Since equation (ii) and (iii) are same we have
 Eigen vectors are of the form
Eigen vectors are of the form
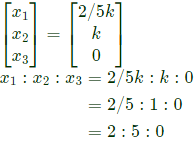
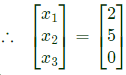 is an eigen vector of matrix p.
is an eigen vector of matrix p.
Q46: In the matrix equation Px = q, which of the following is a necessary condition for the existence of at least on solution for the unknown vector x: (2005)
(a) Augmented matrix [Pq] must have the same rank as matrix P
(b) Vector q must have only non-zero elements
(c) Matrix P must be singular
(d) Matrix P must be square
Ans: (a)
Sol: rank [Pq] = rank [P] is necessary for existence of at least one solution to Px = q.
Q47: The eigen values of the system represented by 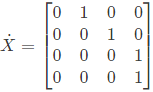 X are (2002)
X are (2002)
(a) 0, 0, 0, 0
(b) 1, 1, 1, 1
(c) 0, 0, 0, -1
(d) 1, 0, 0, 0
Ans: (d)
Q48: The determinant of the matrix 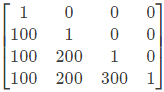 is: (2002)
is: (2002)
(a) 100
(b) 200
(c) 1
(d) 300
Ans: (c)
Sol: The given matrix is alower traingular matrix
Therefore, |A|= Product of its leading diagonal elemetns = (1)(1)(1)(1) = 1
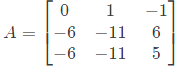 The absolute value of the ratio of the maximum eigenvalue to the minimum eigenvalue is _______. (SET-1 (2014))
The absolute value of the ratio of the maximum eigenvalue to the minimum eigenvalue is _______. (SET-1 (2014))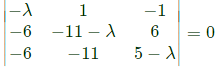
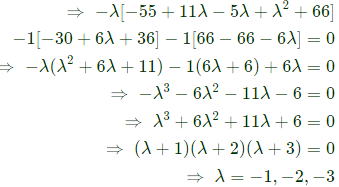 The absolute values of λ are ∣𝜆∣ = 1, 2, 3
The absolute values of λ are ∣𝜆∣ = 1, 2, 3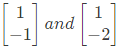 respectively. The matrix is (2013)
respectively. The matrix is (2013)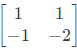
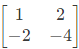
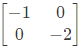
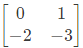
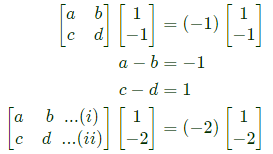
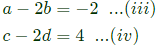 From equation (i) and (iii), a = 0 and b = 1
From equation (i) and (iii), a = 0 and b = 1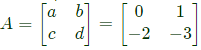
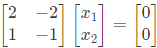 has (2013)
has (2013)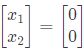
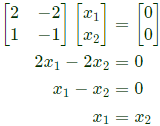 i.e. x1 and x2 are having infinite number of solutions.
i.e. x1 and x2 are having infinite number of solutions. 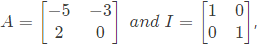 the value of A3 is (2012 )
the value of A3 is (2012 ) Characteristic equation of A is
Characteristic equation of A is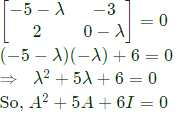 (by Cayley Hamilton theorem)
(by Cayley Hamilton theorem)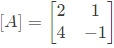 is decomposed into a product of a lower triangular matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and [U] matrices respectively are (2011)
is decomposed into a product of a lower triangular matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and [U] matrices respectively are (2011)
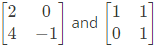
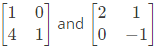
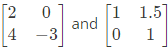
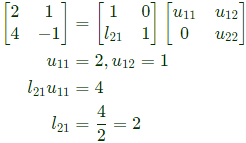
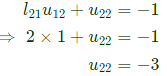 So one possible breakdown is
So one possible breakdown is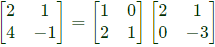 But this is not any of the choises given.
But this is not any of the choises given.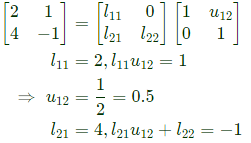
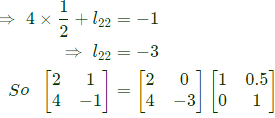
 The augmental matrix is
The augmental matrix is 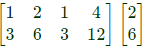
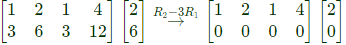 rank(A) = rank(A∣B) = 1
rank(A) = rank(A∣B) = 1 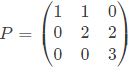 is (2010)
is (2010)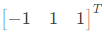
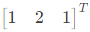
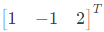
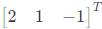
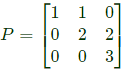
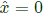
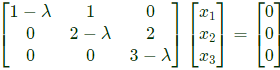 Putting λ1 = 1, we get the eigen vector corresponding to this eigen value,
Putting λ1 = 1, we get the eigen vector corresponding to this eigen value,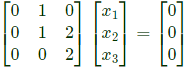 Which gives the equations
Which gives the equations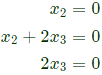 The solution is 𝑥2 = 0, 𝑥3 = 0, 𝑥1= 𝑘
The solution is 𝑥2 = 0, 𝑥3 = 0, 𝑥1= 𝑘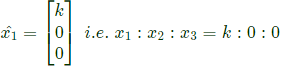
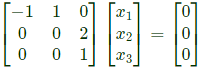 Which gives the equations,
Which gives the equations,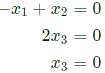 Solution is x3 = 0, x1 = k, x2 = k
Solution is x3 = 0, x1 = k, x2 = k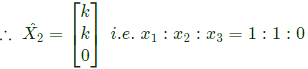 Since none of the eigen vectors given in the choises is of this ratio, we need to proceed further and find 3rd eigen vector also.
Since none of the eigen vectors given in the choises is of this ratio, we need to proceed further and find 3rd eigen vector also.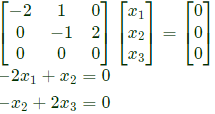
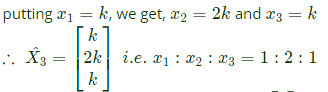 Only the eigen vector geven in choise
Only the eigen vector geven in choise 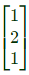 is in this ratio.
is in this ratio. is a real vector
is a real vector  Then, which one of the following statements is correct? (2008)
Then, which one of the following statements is correct? (2008)
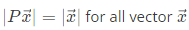
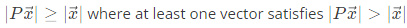
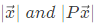
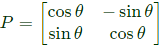 Properly of orthogonal matrix A
Properly of orthogonal matrix A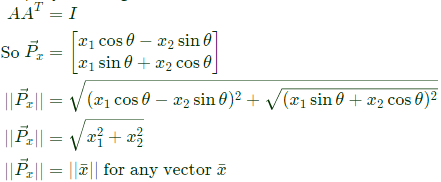
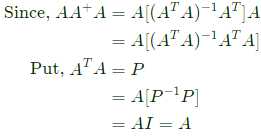
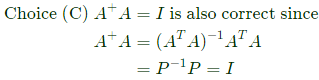
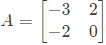 A9 equals (2007)
A9 equals (2007)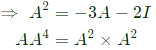

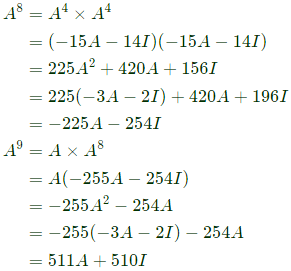
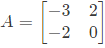 A satisfies the relation (2007)
A satisfies the relation (2007)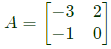
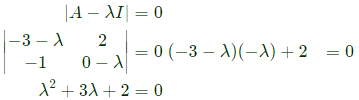 A will satisfy this equation according to cayley hamition theorem
A will satisfy this equation according to cayley hamition theorem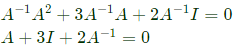
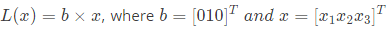 are three dimensional vectors. The 3 x 3 matrix M of this operations satisfies
are three dimensional vectors. The 3 x 3 matrix M of this operations satisfies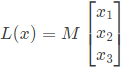 Then the eigenvalues of M are (2007)
Then the eigenvalues of M are (2007)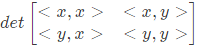 (a) is zero when x and y are linearly independent
(a) is zero when x and y are linearly independent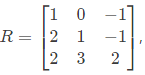 then top row of R−1 is (2005)
then top row of R−1 is (2005)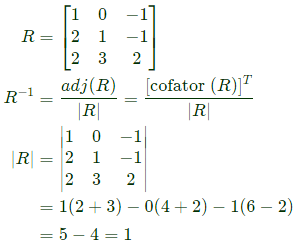 Since we need only the top row of R−1, we need to find only first column of (R) which after transpose will become first row of Adj(A).
Since we need only the top row of R−1, we need to find only first column of (R) which after transpose will become first row of Adj(A). 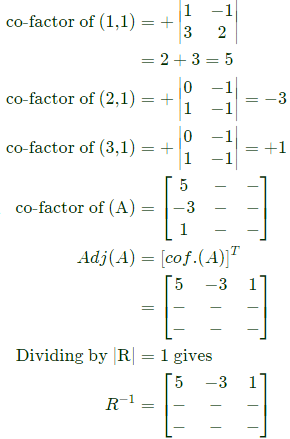
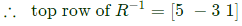
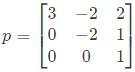 one of the eigen values is equal to -2. Which of the following is an eigen vector ? (2005)
one of the eigen values is equal to -2. Which of the following is an eigen vector ? (2005)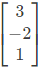
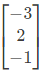

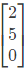
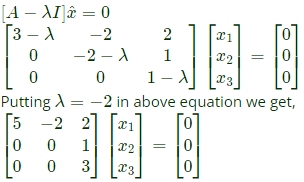 Which gives the equations,
Which gives the equations,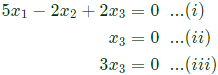 Since equation (ii) and (iii) are same we have
Since equation (ii) and (iii) are same we have Eigen vectors are of the form
Eigen vectors are of the form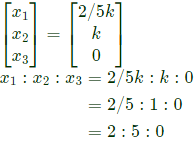
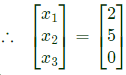 is an eigen vector of matrix p.
is an eigen vector of matrix p.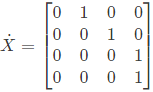 X are (2002)
X are (2002)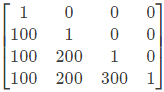 is: (2002)
is: (2002)




















