Class 9 Maths Chapter 4 Previous Year Questions - Linear Equations in Two Variables
Very Short Answer Type Questions
Q1. Write whether the following statements are True or False? Justify your answers. [2025]
(i) ax + by + c, where a, b and c are real numbers, is a linear equation in two variables.
(ii) A linear equation 2x + 3y = 5 has a unique solution.
(iii) All the points (2, 0), (–3, 0), (4, 2) and (0, 5) lie on the x-axis.
(iv) The line parallel to y-axis at a distance 4 units to the left of y-axis is given by the equation x = –4.
(v) The graph of the equation y = mx + c passes through the origin.
 View Answer
View Answer 
(i) False. [Because ax + by + c = 0 is a linear equation in two variables if both ‘a‘ and ‘b’ are non-zero.]
(ii) False. [Because a linear equation in two variables has infinitely many solutions.]
(iii) False. [Because the points (2, 0) and (–3, 0) lie on the x-axis, (0, 5) lie on the y-axis whereas the point (4, 2) lies in the first quadrant.]
(iv) True.
(v) False. [Because the point (0, 0) i.e., x = 0 + y = 0 does not satisfy the equation]
Q2. Write whether the following statement is True or False? Justify your answer. [2024]
The coordinates of points given in the table:

Represent some of the solutions of the equation 2x + 2 = y.
 View Answer
View Answer 
True. [Since, on looking at the given coordinates, we observe that each y-coordinate is two units more than double the x-coordinate.]
Q3. Look at the following graphical representation of an equation. Which of the following is not its solution? [2022]
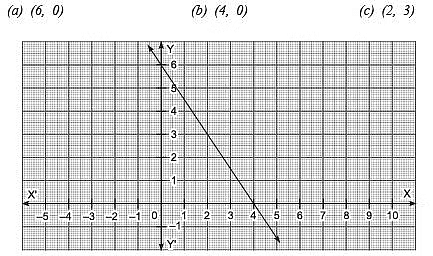
 View Answer
View Answer 
The point (6, 0) does not lie on the graph.
∴ The point (6, 0) is not the solution of the equation.
Short Answer Type Questions
Q1. Is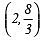 a solution of 2x + 3y = 12? [2025]
a solution of 2x + 3y = 12? [2025] View Answer
View Answer 
The given equation is 2x + 3y = 12 ...(1)
Here Solution = 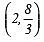
⇒ x = 2 and y = (8/3)
Substituting x = 2 and y =(8/3) in (1), we get
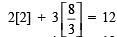 ⇒ 4 + 8 = 12⇒ 12 = 12∵ L.H.S. = R.H.S
⇒ 4 + 8 = 12⇒ 12 = 12∵ L.H.S. = R.H.S
∴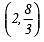 is a solution of 2x + 3y = 12.
is a solution of 2x + 3y = 12.
Q2. Write two solutions of 3x + y = 8. [2023]
 View Answer
View Answer 
We have 3x + y = 8
For x = 0, we have 3(0) + y = 8
⇒ 0 x y= 8 ⇒ y = 8
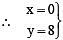 .e. (0, 8) is a solution.For x = 1, we have 3(1) + y = 8⇒ 3 + y = 8⇒ y = 8 – 3 = 5
.e. (0, 8) is a solution.For x = 1, we have 3(1) + y = 8⇒ 3 + y = 8⇒ y = 8 – 3 = 5
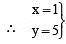 i.e. (1, 5) is another solution.
i.e. (1, 5) is another solution.
Q3. If x = –1 and y = 2 is a solution of kx + 3y = 7, find the value k. [2022]
 View Answer
View Answer 
We have kx + 3y = 7 ...(1)
∴ Putting x = –1 and y = 2 in (1), we get
k(–1) + 3(2) = 7
⇒ –k + 6 = 7
⇒ –k = 7 – 6 = 1
⇒ k= –1
Thus, the required value of k = –1.
Q4. Show that x = 2 and y = 1 satisfy the linear equation 2x + 3y = 7. [2020]
 View Answer
View Answer 
We have 2x + 3y = 7 ...(1)
Since, x = 2 and y = 1 satisfy the equation (1).
∴ Substituting x = 2 and y = 1 in (1), we get
L.H.S. = 2(2) + 3(1) = 4 + 3 = 7
= R.H.S.
Since, L.H.S. = R.H.S.
∴ x = 2 and y = 1 satisfy the given equation.
Long Answer Type Questions
Q1. The taxi fare in a town is ₹10 for the first kilometre and ₹ 6 per km for the subsequent distance. Taking the distance as ‘x’ km and total fare as ₹y, write a linear equation for this information, what will be the total fare for 15 km? [2024]
 View Answer
View Answer 
∵ Total distance is x km.
Total fare = ₹y
∴ x = 1 + (x – 1) = First km + Subsequent distance
Since, fare the first km = ₹10
∴ Fare for the remaining distance = ₹6 x (x – 1) = ₹6x – ₹6
⇒ Total fare = ₹10 + ₹6x – ₹6
= ₹4 + ₹6x
∴ y = 4 + 6x
⇒ y – 6x = 4
⇒ 6x – y + 4 = 0
Which is the required equation.
Now, total fare for 15 km:
6 x 15 – y + 4 = 0 [Substituting x = 15]
⇒ 90 – y + 4 = 0
⇒ 94 – y = 0
⇒ y = 94
∴ Total fare = ₹94.
Q2. Draw the graph x + 2y = 6 and from the graph, find the value of x when y = – 3. [2023]
 View Answer
View Answer 
We have: x + 2y = 6
⇒ 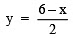 When x = 0, then
When x = 0, then 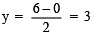 When x = 2, then
When x = 2, then 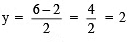 When x = 4, then
When x = 4, then 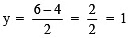
We get the following table of values of x and y.
x | 0 | 2 | 4 |
y | 3 | 2 | 1 |
(x, y) | (0, 3) | (2, 2) | (4, 1) |
Plotting the ordered pairs (0, 3), (2, 2) and (4, 1) and then joining them, we get the graph of x + 2y = 6 as shown below:
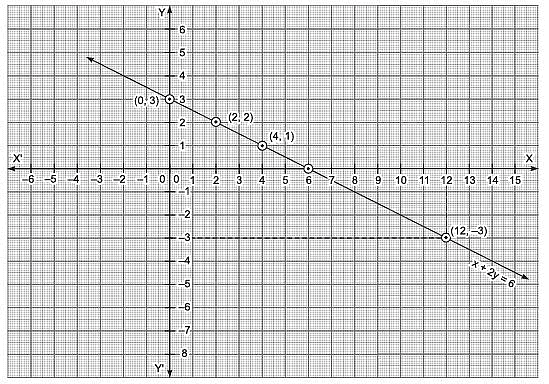
From the graph, we find that for y = – 3, the value of x = 12.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 4 Previous Year Questions - Linear Equations in Two Variables
| 1. What are linear equations in two variables? |  |
| 2. How can we solve linear equations in two variables? |  |
| 3. What is the graphical representation of a linear equation in two variables? |  |
| 4. What are the different forms of linear equations in two variables? |  |
| 5. How do we determine if two linear equations are consistent or inconsistent? |  |

















