Previous Year Questions: Numerical Method | Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE) PDF Download
Q1: Using Newton-Raphson method, a root correct to 3 decimal places of x3−3x−5 = 0 (2017)
(a) 2.222
(b) 2.275
(c) 2.279
(d) None of the above
Ans: (c)
Sol: f(x) = x3 - 3x - 5 and f'(x) = 3x2 - 3, beginning with x0 = 3, the iterates are given in Table 2 which show a stop at iteration no. 5 since the error is x5 - x4 < 10-5 resulting in a root of x* = 2.27902, see figure 2.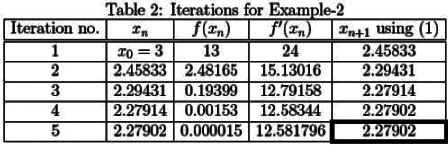
Q2: What is the sum to infinity of the series,
3 + 6x2 + 9x4 + 12x6 +… given ∣x∣ < 1 (2016)
(a) 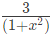 (b)
(b) 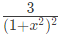 (c)
(c) 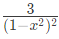 (d)
(d) 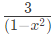 Ans: (c)
Ans: (c)
Sol: S(n) = 3 + 6x2 + 9x4 + 12x6 + ..
−x2S(n) = −3x2 − 6x4 − 9x6− ...
(1 − x2)S(n) = 3 + 3x2 + 3x4 + 3x6 + ...
(1 − x2)S(n) = 3(1 + x2 + x4 + x6 +...)
(1 − x2)S(n) = 3 × (1/(1−x2)) this series is a GP having infinite number and it a = 1 and r = x (i.e < 1)
S(n) = 3/(1 - x2)2
So Answer will be C.
Q3: The velocity v (in kilometer/minute) of a motorbike which starts from rest, is given at fixed intervals of time t (in minutes) as follows: The approximate distance (in kilometers) rounded to two places of decimals covered in 20 minutes using Simpson's 1/3rd rule is ______. (2015 SET-3)
The approximate distance (in kilometers) rounded to two places of decimals covered in 20 minutes using Simpson's 1/3rd rule is ______. (2015 SET-3)
(a) 225
(b) 310
(c) 360
(d) 420
Ans: (b)
Sol: The total distance covered is given by the area under the speed curve and can be calculated by integrating the speed curve equation in the given range. In the question, exact speed function is not given, but the speed at different time instants is given.
Question is asking the distance covered in 20 minutes. According to the question, the motion starts at t = 0 and ends at t = 20. So the speed function has to be integrated in the range t = 0 to t = 20. Therefore an additional point (t = 0) has to be considered while integrating. After adding t = 0, number of points will be 11 and number of intervals will be 10. And the answer will be 309.33.
Distance
S = ((b−a)/3n) [f(0) + 4(f(2) + f(6) + f(10) + f(14) + f(18)) + 2(f(4) + f(8) + f(12) + f(16) + f(20))]
= 2/3 [0 + 4(10 + 25 + 32 + 11 + 2) + 2(18 + 29 + 20 + 5)]
= 309.33
Q4: The secant method is used to find the root of an equation f(x) = 0. It is started from two distinct estimates xa and xb for the root. It is an iterative procedure involving linear interpolation to a root. The iteration stops if f(xb) is very small and then xb is the solution. The procedure is given below. Observe that there is an expression which is missing and is marked by ?. Which is the suitable expression that is to be put in place of ? so that it follows all steps of the secant method? (2015 SET-2) (a) xb − (fb − f(xa))fb/(xb − xa)
(a) xb − (fb − f(xa))fb/(xb − xa)
(b) xa − (fb − f(xa))fa/(xb − xa)
(c) xb − (xb − xa)fb/(fb − f(xa))
(d) xa − (xb− xa)fa/(fb − f(xa))
Ans: (c)
Sol: Also, xb − (xb − xa)fb/(fb − f(xa)) = (xafb − xbf(xa))/(fb − f(xa))
Q5: With respect to the numerical evaluation of the definite integral, 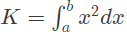 , where a and b are given, which of the following statements is/are TRUE?
, where a and b are given, which of the following statements is/are TRUE?
(I) The value of K obtained using the trapezoidal rule is always greater than or equal to the exact value of the definite integral.
(II) The value of K obtained using the Simpson's rule is always equal to the exact value of the definite integral. (2014 SET-3)
(a) I only
(b) II only
(c) Both I and II
(d) Neither I nor II
Ans: (c)
Sol: 1 is true because when we find the true error for the given function in case of Trepoziadal rule we get E = -h3/6 which is always less than zero. Here the error is = True value - Approx Value. Since the error is less than zero the approx value K is always greater than exact value.
2.Since the given function is a polynomial of degree 2 Simpson's will provide the exact value(Simpson's will give the exact value if the degree of the polynomial is < = 3).
Q6: In the Newton-Raphson method, an initial guess of x0 = 2 is made and the sequence x0, x1, x2... is obtained for the function
0.75x3 − 2x2 − 2x + 4 = 0
Consider the statements
(I) x3 = 0.
(II) The method converges to a solution in a finite number of iterations.
Which of the following is TRUE? (2014 SET-2)
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Ans: (a)
Sol: xn+1 = 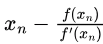 for Newton-Raphson method (See the link below)
for Newton-Raphson method (See the link below)
f(x) = 0.75x3−2x2 − 2x + 4
⇒ f(2) = −2
f′(x) = 2.25x2 − 4x − 2
⇒ f′(2) = 9 − 8 − 2 = −1
So, 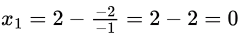
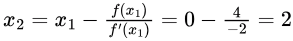 Since x2 = x0, we will get x3 = x1 = 0.
Since x2 = x0, we will get x3 = x1 = 0.
So, x3 = 0, and the method never converges. A choice.
Q7: The Guass-Seidal iterative method can be used to solve which of the following sets? (2013)
(a) Linear algebraic equations
(b) Linear and non-linear algebraic equations
(c) Linear differential equations
(d) Linear and non-linear differential equations
Ans: (a)
Sol: The Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations.
Q8: Function f is known at the following points: The value of
The value of 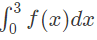 computed using the trapezoidal rule is (2013)
computed using the trapezoidal rule is (2013)
(a) 8.983
(b) 9.003
(c) 9.017
(d) 9.045
Ans: (d)
Sol: = Δx/2(f(0) + 2(f(0.3) + .... + f(2.7)) + f(3.0))
= 0.15(0 + 2(0.09 + 0.36 + 0.81 + 1.44 + 2.25 + 3.24 + 4.41 + 5.76 + 7.29) + 9.00)
= 9.045
Q9: The bisection method is applied to compute a zero of the function f(x) = x4−x3−x2−4 in the interval [1,9]. The method converges to a solution after _____iterations. (2012)
(a) 1
(b) 3
(c) 5
(d) 7
Ans: (b)
Sol: Bisection method is exactly like binary search on a list.
In bisection method, in each iteration, we pick the mid point of the interval as approxiamation of the root, and see where are we, i.e. should we choose left sub-interval, or right-subinterval, and we continue until we find the root, or we reach some error tolerance.
So in first iteration, our guess for root is mid point of [1,9] i.e. 5. Now f(5) > 0, so we choose left sub-interval [1,5] (as any value in right sub-interval [5,9] would give more positive value of f).
In second iteration, we choose mid point of [1,5] i.e. 3, but again f(3) > 0, so we again choose left sub-interval [1,3].
In third iteration, we choose mid point of [1,3] i.e. 2, now f(2) = 0
So we found root in 3 iterations. So answer is option (B).
Q10: Given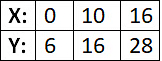 The interpolated value X=4 using piecewise linear interpolation is (2011)
The interpolated value X=4 using piecewise linear interpolation is (2011)
(a) 11
(b) 4
(c) 22
(d) 10
Ans: (d)
Sol: Piece wise linear interpolation is a simple way of connecting points through straight lines
So equation Of line joining first 2 points is
Y - x = 6
So at x = 4 , y is 10
Q11: Newton-Raphson method is used to compute a root of the equation x2 − 13 = 0 with 3.5 as the initial value. The approximation after one iteration is (2010)
(a) 3.575
(b) 3.676
(c) 3.667
(d) 3.607
Ans: (d)
Sol: x = 3.5 - ((3.52)-13)/(2*3.5) so x = 3.607 it is from the next term formula of newton raphson method.
|
34 videos|123 docs|72 tests
|
FAQs on Previous Year Questions: Numerical Method - Engineering Mathematics for Computer Science Engineering - Computer Science Engineering (CSE)
| 1. How is numerical method used in computer science engineering? |  |
| 2. What are some common numerical methods used in computer science engineering? |  |
| 3. How does the Newton-Raphson method work in numerical methods? |  |
| 4. What is the importance of numerical methods in computer science engineering? |  |
| 5. How do numerical methods help in improving computational efficiency in computer science engineering? |  |
|
34 videos|123 docs|72 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|


















