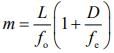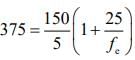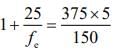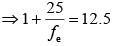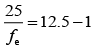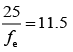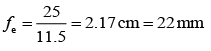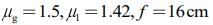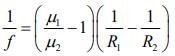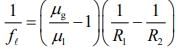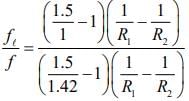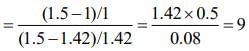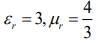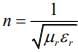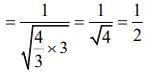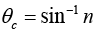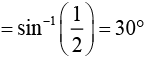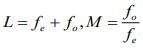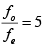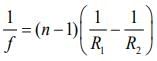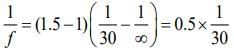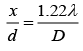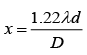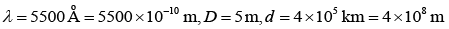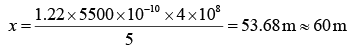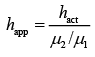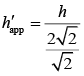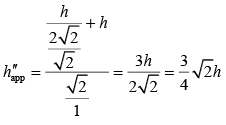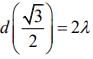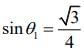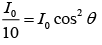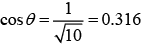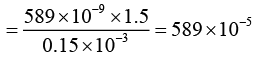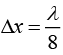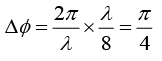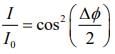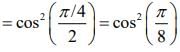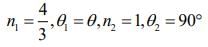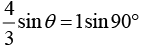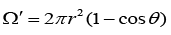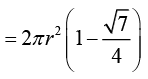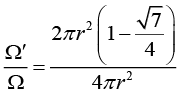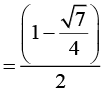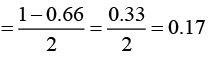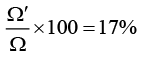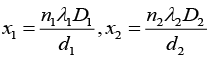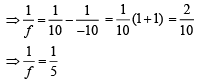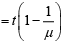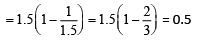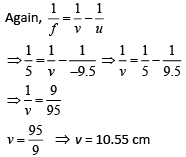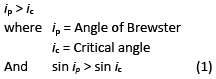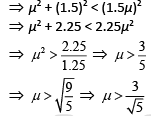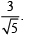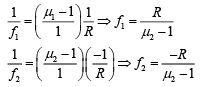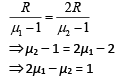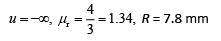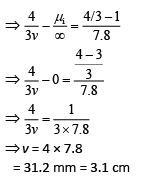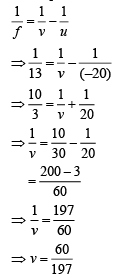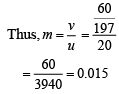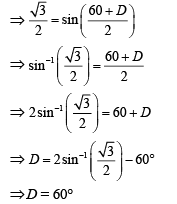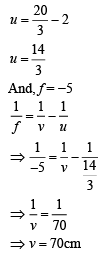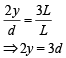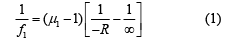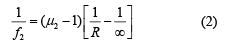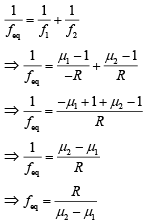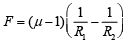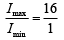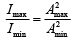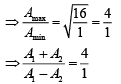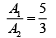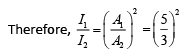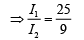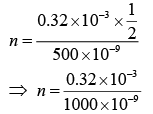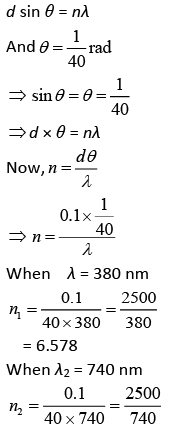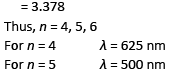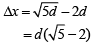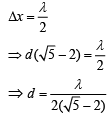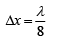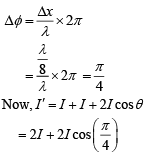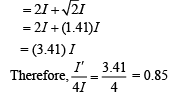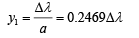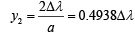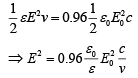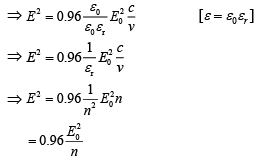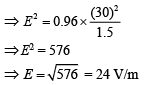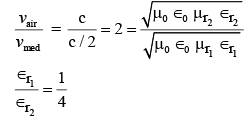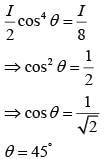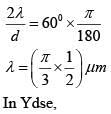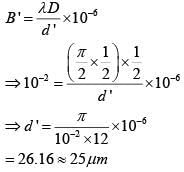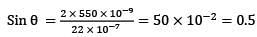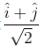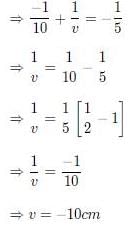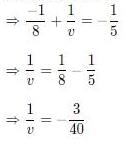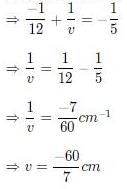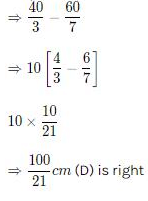JEE Main Previous Year Questions (2016- 2025): Ray & Wave Optics- 1 | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. If we need a magnification of 375 from a compound microscope of tube length 150 mm and an objective of focal length 5 mm, the focal length of the eye-piece, should be close to (2020)
(a) 22 mm
(b) 12 mm
(c) 2 mm
(d) 33 mm
Ans. (a)
Given that m = 375, fo = 5 mm and L = 150 mm.
Magnification of compound microscope is given by
Where L is length of tube, D is near point of eye D = 25 cm, fo is focal length of objective and fe focal length of eye piece. So,
Q.2. A thin lens made of glass (refractive index = 1.5) of focal length f = 16 cm is immersed in a liquid of refractive index 1.42. If its focal length in liquid is fl, then the ratio fl/f is closest to the integer (2020)
(a) 1
(b) 9
(c) 5
(d) 17
Ans. (2)
Given that,
According to Lens Maker’s formula, we have
For air, we have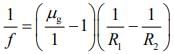
For liquid, we have
So,
Q.3. The critical angle of a medium for a specific wavelength, if the medium has relative permittivity 3 and relative permeability 4/3 for this wavelength, will be (2020)
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Ans. (b)
Given that
Reflective index is given by
Critical angle is given by
Q.4. The magnifying power of a telescope with tube length 60 cm is 5. What is the focal length of its eye piece? (2020)
(a) 20 cm
(b) 40 cm
(c) 30 cm
(d) 10 cm
Ans. (d)
Let length of the tube, focal length of eye piece lens and focal length of objective lens be L, fe and fo respectively.
We know that
Given that L = 60cm, M = 5
So, fo +fe= 60 ....................... (1)
f0 = 5fe ............... (2)
From Eqs. (1) and (2), we get
fe = 10cm, f0 = 50cm
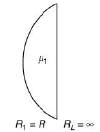
Q.5. A point object in air is in front of the curved surface of a plano-convex lens. The radius of curvature of the curved surface is 30 cm and the refractive index of the lens material is 1.5, then the focal length of the lens (in cm) is _______. (2020)
Ans. (60)
Given that n = 1.5, R1 = 30cm, R2 = ∞
From lens maker formula, we have
f = 60 cm
Q.6. An object is gradually moving away from the focal point of a concave mirror along the axis of the mirror. The graphical representation of the magnitude of linear magnification (m) versus distance of the object from the mirror (x) is correctly given by (Graphs are drawn schematically and are not to scale) (2020)
(a)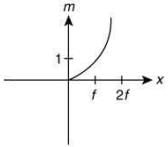
(b)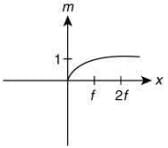
(c)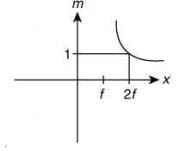
(d) 
Ans. (c)
Lens formula is given by.............. (1)
Magnification is given by m = v/u ............. (2)
At u = f Eqs. (1) and (2) becomes
v = ∞, m = ∞
At u = 2f Eqs. (1) and (2) becomes
v = -2f, m = −1
So, only graph of option (3) satisfy the conditions.
Q.7. The aperture diameter of a telescope is 5 m. The separation between the moon and the earth is 4 × 105 km. With light of wavelength of 5500 Å, the minimum separation between objects on the surface of moon, so that they are just resolved, is close to (2020)
(a) 60 m
(b) 20 m
(c) 200 m
(d) 600 m
Ans. (a)
For just resolved the angular separation is given by.................. (1)
Where D is aperture diameter of a telescope.
Let distance between object and surface of the moon be x and distance between earth and moon be d. So, θ = x/d ............ (2)
From Eqs. (1) and (2), we get
Given that
Therefore,
Q.8. A vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be (2020)
(a)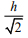
(b)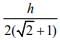
(c)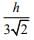
(d)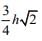
Ans. (d)
Given condition is shown in the following figureApparent depth of the bottom of the vessel is given by
Apparent depth of the bottom between two liquids, that is, at height h from bottom is
Apparent depth of the bottom at the top of the vessel, that is, at height 2h from bottom is
Q.9. Visible light of wavelength 6000 × 10−8 cm falls normally on single slit and produces a diffraction pattern. It is found that the second diffraction minimum is at 60° from the central maximum. If the first minimum is produced at θ1, then θ1 is close to (2020)
(a) 20°
(b) 30°
(c) 25°
(d) 45°
Ans. (c)
Given that λ = 6000 x 10-8cm, θ2 = 60°
nth minima of diffraction is given by dsinθ = nλ
For 2nd minima n = 2, we have d sin 60° = 2λ............. (1)
For 1st minima n = 1, we have d sinθ1 = λ
sinθ1 = λ/d
From Eq. (1), we get
=> θ ∼ 25°
Q.10. A polarizer – analyser set is adjusted such that the intensity of light coming out of the analyser is just 10% of the original intensity. Assuming that the polarizer – analyser set does not absorb any light, the angle by which the analyser need to be rotated further to reduce the output intensity to be zero, is (2020)
(a) 71.6°
(b) 18.4°
(c) 90°
(d) 45°
Ans. (b)
Given that I = I0/10 ............ (1)
Where I0 is original intensity
According to Malus Law, we have I = I0cos2θ ............ (2)
From Eqs. (1) and (2), we get
θ = 71.57°
So, angle by which analyzer need to be rotated to reduce output intensity to zero is
α = 90 −θ = 90 - 71.57 = 18.43°
Q.11. In a Young’s double slit experiment, the separation between the slits is 0.15 mm. In the experiment, a source of light of wavelength 589 nm is used and the interference pattern is observed on a screen kept 1.5 m away. The separation between the successive bright fringes on the screen is (2020)
(a) 6.9 mm
(b) 3.9 mm
(c) 5.9 mm
(d) 4.9 mm
Ans. (c)
Given that, λ = 589 nm = 589 x 10-9 m , d = 0.15 mm = 0.15 x 10-3 m and D = 1.5 m.
We know, separation between the successive bright fringes is given by x = λD/d
= 5.89 mm ~ 5.9 mm
Q.12. In a double-slit experiment, at a certain point on the screen, the path difference between the two interfering waves in (1/8)th of a wavelength. The ratio of the intensity of light at that point to that at the centre of a bright fringe is (2020)
(a) 0.853
(b) 0.672
(c) 0.568
(d) 0.760
Ans. (a)
Given that
So,
Intensities at phase difference is given by
= 0.853
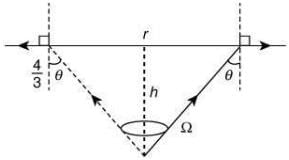
Q.13. There is a small source of light at some depth below the surface of water (refractive index = 4/3) in a tank of large cross sectional surface area. Neglecting any reflection from the bottom and absorption by water, percentage of light that emerges out of surface is (nearly) [Use the fact that surface area of a spherical cap of height h and radius of curvature r is 2πrh] (2020)
(a) 21%
(b) 34%
(c) 17%
(d) 50%
Ans. (c)
Let the angle of incident of light on surface of water be θ.
Given conditions is shown by following figure
Since, there is total internal reflection.
From Snell’s law, we have n1sinθ1 = n2sinθ2
Here
So,
Sin θ = 3/4
And cos θ = √7/4
Area of sphere where light spread is given by Ω = 4πr2
The area of a spherical cap (at the surface) is given by
The percentage of light that emerges out of surface is given by
Q.14. In a Young’s double slit experiment, 15 fringes are observed on a small portion of the screen when light of wavelength 500 nm is used. Ten fringes are observed on the same section of the screen when another light source of wavelength λ is used. Then the value of λ is (in nm)___________. (2020)
Ans. (750)
Given that λ1 = 500 nm, n1 = 15,n2 = 10
Distance of nth fringe from the centre is given by
Where D is the distance of screen from slits and d is the distance between slits.
So,
Since, x1 = x2 , D1 = D2, d1 = d2
Therefore, n1λ1 = n2λ2
15 x 500 = 10 x λ2
λ2 = 7500/10 = 750 nm
Q.15. A convex lens is put 10 cm from a light source and it makes a sharp image on a screen, kept 10 cm from the lens. Now a glass block (refractive index 1.5) of 1.5 cm thickness is placed in contact with the light source. To get the sharp image again, the screen is shifted by a distance d. Then d is (2019)
(a) 1.1 cm away from the lens.
(b) 0
(c) 0.55 cm towards the lens.
(d) 0.55 cm away from the lens.
Ans. (d)
Distance of convex lens from source of light, u = −10 cm
Distance of convex lens from screen, v = 10 cm
Refractive index, μ = 1.5 Thickness of glass, t = 1.5 cm
Therefore, f = 5 cm
Now, the slab is shifted in the direction of incident ray
Distance of convex lens from source of light, u = −(10 – 0.5) = –9.5 cm
Hence, the screen is shifted 0.55 cm away from the lens.
Q.16. Consider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index μ. A student finds that, irrespective of what the incident angle i (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is (2019)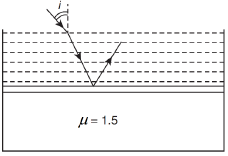
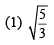
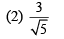
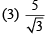
(4) 4/3
Ans. (2)
As we know that,
According to Brewester’s law,
Putting this value in Eq. (1), we get
sin ic < sin ip
Squaring both the sides, we get
Thus, the minimum value of μ is
Q.17. Two plane mirrors are inclined to each other such that a ray of light incident on the first mirror (M1) and parallel to the second mirror (M2) is finally reflected from the second mirror (M2) parallel to the first mirror (M1). The angle between the two mirrors will be (2019)
(a) 45°
(b) 60°
(c) 75°
(d) 90°
Ans. (b)
Let θ be the angle between two mirrors.As we know that, sum of angle of triangle = 180°
θ + θ + θ = 180°
⇒ 3θ = 180°
⇒ θ = 60°
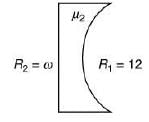
Q.18. A plano-convex lens of refractive index μ1 and focal length f1 is kept in contact with another plano-concave lens of refractive index μ2 and focal length f2. If the radius of curvature of their spherical faces is R each and f1 = 2f2, then μ1 and μ2 are related as (2019)
(a) μ1 + μ2 = 3
(b) 2μ1 – μ2 = 1
(c) 3μ2 − 2μ1 = 1
(d) 2μ2 – μ1 = 1
Ans. (b)
We have, f1 = 2f2 (1)We know that
Put these values in Eq. (1), we get
Q.19. The eye can be regarded as a single refracting surface. The radius of curvature of this surface is equal to that of cornea (7.8 mm). This surface separates two media of refractive indices 1 and 1.34. Calculate the distance from the refracting surface at which a parallel beam of light will come to focus. (2019)
(a) 1 cm
(b) 2 cm
(c) 4.0 cm
(d) 3.1 cm
Ans. (d)
We have,It is given that
Q.20. An object is at a distance of 20 m from a convex lens of focal length 0.3 m. The lens forms an image of the object. If the object moves away from the lens at a speed of 5 m/s, the speed and direction of the image will be (2019)
(a) 1.16 × 10−3 m/s towards the lens.
(b) 3.22 × 10−3 m/s towards the lens.
(c) 0.92 × 10−3 m/s away from the lens.
(d) 2.26 × 10−3 m/s away from the lens.
Ans. (1)
Lens equation is,
Therefore, v1 = m2v0
= (0.015)2 (−5)
= 1.15 × 10−3 towards the lens
Q.21. The variation of refractive index of a crown glass thin prism with wavelength of the incident light is shown. Which of the following graphs is the correct one, if Dm is the angle of minimum deviation? (2019)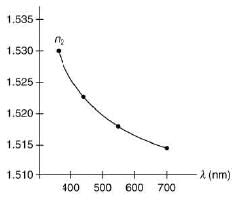
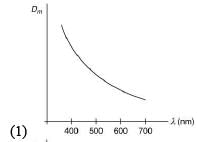
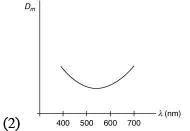

Ans. (1)
We have,
Dm = (μ – 1)A
Since, on increasing the wavelength, μ decreases and hence Dm decreases.
Q.22. A monochromatic light is incident at a certain angle on an equilateral triangular prism and suffers minimum deviation. If the refractive index of the material of the prism is √3, then the angle of incidence is (2019)
(a) 90°
(b) 30°
(c) 60°
(d) 45°
Ans. (c)
As we know that refractive index is given as
Q.23. What is the position and nature of image formed by lens combination shown in figure? (f1, f2 are focal lengths) (2019)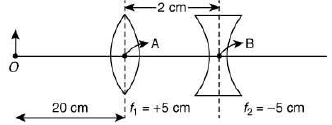 (a) 70 cm from point B at right; virtual.
(a) 70 cm from point B at right; virtual.
(b) 40 cm from point B at right; real.
(c) 20/3 cm from point B at right, real.
(d) 70 cm from point B at right; real.
Ans. (d)
As we know that lens formula is
For second lens refraction,
Therefore, 70 cm from B at right, real.
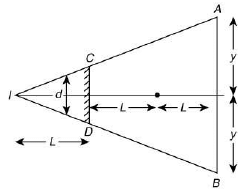
Q.24. A point source of light, S is placed at a distance L in front of the center of plane mirror of width d which is hanging vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror, at a distance 2L as shown below. The distance over which the man can see the image of the light source in the mirror is (2019)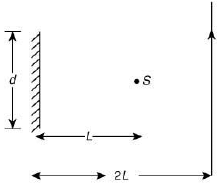 (a) d
(a) d
(b) 2d
(c) 3d
(d) d/2
Ans. (c)
Consider ΔICD and ΔIAB.
Since, both are similar triangle so, ratio of identical side of triangle are equal.
Q.25. A plano-convex lens (focal length f2, refractive index μ2, radius of curvature R) fits exactly into a plano-concave lens (focal length f1, refractive index μ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be (2019)
(1) f1 – f2 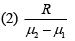
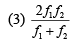
(4) f1 + f2
Ans. (2)
For plano-convex lens:
For plano-concave lens
When both lenses are combined:
Q.26. Formation of real image using a biconvex lens is shown in the figure. If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the screen? (2019)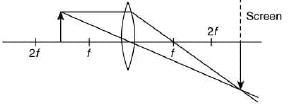 (a) Image disappears
(a) Image disappears
(b) Magnified image
(c) Erect real image
(d) No change
Ans. (a)
Focal length
Since, whole set up is immersed in water without disturbing the object and screen position. Thus, focal length of lens will change hence image disappear from the screen.
Q.27. Two coherent sources produce waves of different intensities which interfere. After interference, the ratio of the maximum intensity to the minimum intensity is 16. The intensity of the waves is in the ratio (2019)
(a) 16 : 9
(b) 25 : 9
(c) 4 : 1
(d) 5 : 3
Ans. (b)
The ratio of the maximum intensity to the minimum intensity
We know that,
where, Amax and Amin are the maximum and minimum amplitudes of the wave.
Using componendo and dividendo rule, we have
Thus, the required ratio is 25 : 9.
Q.28. In a Young’s double-slit experiment, the slits are placed 0.320 mm apart. Light of wavelength λ = 500 nm is incident on the slits. The total number of bright fringes that are observed in the angular range −30° ≤ θ ≤ 30° is (2019)
(a) 640
(b) 320
(c) 321
(d) 641
Ans. (b)
Given λ = 500 nm, d = 0.32 mm, θ = 30°
Path difference
dsinθ = nλ
0.32 × 10−3sin30° = n × 500 × 10−9
Therefore, n = 320
Q.29. In a Young’s double-slit experiment with slit separation 0.1 mm, one observes a bright fringe at angle 1/40 rad by using light of wavelength λ1. When the light of wavelength λ2 is used, a bright fringe is seen at the same angle in the same set up. Given that λ1 and λ2 are in visible range (380 nm to 740 nm), their values are (2019)
(a) 625 nm, 500 nm
(b) 380 nm, 525 nm
(c) 380 nm, 500 nm
(d) 400 nm, 500 nm
Ans. (a)
Path difference is given by
Q.30. Consider a Young’s double-slit experiment as shown in figure. What should be the slit separation d in terms of wavelength λ such that the first minima occurs directly in front of the slit (S1)? (2019)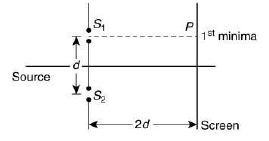
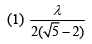
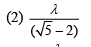
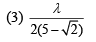
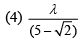
Ans. (1)
At point P we have
For first minima we know that,
Q.31. In a Young’s double-slit experiment, the path difference, at a certain point on the screen, between two interfering waves is 1/8th of wavelength. The ratio of the intensity at this point to that at the center of a bright fringe is close to (2019)
(a) 0.94
(b) 0.80
(c) 0.74
(d) 0.85
Ans. (d)
Let I be the intensity of each wave
Q.32. In a double-slit experiment, green light (5303Å) falls on a double slit having a separation of 19.44 μm and a width of 4.05 μm. The number of bright fringes between the first and the second diffraction minima is (2019)
(a) 10
(b) 05
(c) 04
(d) 09
Ans. (b)
For diffraction, first minima is
Second minima is
For interference, path difference at P
Path difference at Q
So, order of maxima is 5, 6, 7, 8, 9
Therefore, 5 bright fringes are there between the first and second diffraction minima.
Q.33. A light wave is incident normally on a glass slab of refractive index 1.5. If 4% of light gets reflected and the amplitude of the electric field of the incident light is 30 V/m, then the amplitude of the electric field for the wave propagating in the glass medium will be (2019)
(a) 30 V/m
(b) 10 V/m
(c) 24 V/m
(d) 6 V/m
Ans. (c)
Let I be the incident energy and I' be the reflected incident energy.
I' = 0.96I
Incident energy in airIncident energy in glass
Put these values in Eq. (1), we get
Q.34. An EM wave from air enters a medium. The electric fields are  in air and
in air and 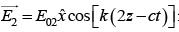 in medium, where the wave number k and frequency v refer to their values in air. The medium is non-magnetic. ∈r1 and ∈r2 refer to relative permitivities of air and medium respectively.
in medium, where the wave number k and frequency v refer to their values in air. The medium is non-magnetic. ∈r1 and ∈r2 refer to relative permitivities of air and medium respectively.
which of the following options is correct ? [2018]
(a) 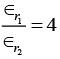
(b) 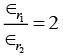
(c) 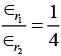
(d) 
Ans: (c)
Q.35. Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be 1/2. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be 1/8 The angle between polarizer A and C (in degrees) is: [2018]
(a) 0
(b) 30
(c) 45
(d) 60
Ans: (c)
Unpolarized light of intensity I, when passed through a polarizer A, its intensity becomes I/2
Since intensity of light emerging from polarizer B = I/2
So, A & B are parallel placed.
Let, C makes angle θ with A.
So,
Q.36. The angular width of the central maximum in a single slit diffraction pattern is 600. The width of the slit is 1 μm. The slit is illuminated by monochromatic plane waves. If another slit of same width is made near it, Young’s fringes can be observed on a screen placed at a distance of 50 cm from the slits. If the observed fringe width is 1 cm, what is slit separation distance ?
(i.e. distance between the centres of each slit.) [2018]
(a) 25 μm
(b) 50 μm
(c) 75 μm
(d) 100 μm
Ans: (a)
Q.37. Light of wavelength 550 nm falls normally on a slit of width 22.0 x 10-5 cm. The angular position of the second minima from the central maximum will be (in radians): [2018]
(a) π/8
(b) π/12
(c) π/6
(d) π/4
Ans: (c)
b sin θ = nλ
b sin θ = 2λ
sin θ = 1/2
θ = π/6
Q.38. A monochromatic beam of light has a frequency v = 3/2π × 1012 Hz and is propagating along the direction 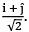 It is polarized along the
It is polarized along the 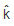 direction. The acceptable form for the magnetic field is:
direction. The acceptable form for the magnetic field is: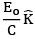 [2018]
[2018]
(a) 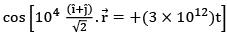
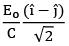
(b) 
(c) 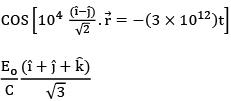
(d)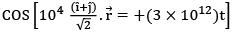
Ans: (b)
Wave propagation vector should be along
So, 2 is the only option which satisfies the above condition.
Q.39. A particle is oscillating on the X-axis with an amplitude 2 cm about the point x0 = 10 cm, with a frequency ω. A concave mirror of focal length 5 cm is placed at the origin (see figure). [2018]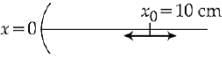
Identify the correct statements.
(A) The image executes periodic motion.
(B) The image executes non-periodic motion.
(C) The turning points of the image are asymmetric w.r.t. the image of the point at x =10 cm.
(D) The distance between the turning points of the oscillation of the image is 100/21 cm.
(a) (A), (D)
(b) (A), (C), (D)
(c) (B), (C)
(d) (B), (D)
Ans: (b)
For mean
As image copies the time period of object (A) is right as well. It will be periodic motion
For one extreme
Right arrow = -40/3 cm
for other extreme
These points are asymmetric about x0 = 10 cm So, (c) is right
Amplitude of oscillation of image
|
201 videos|410 docs|280 tests
|