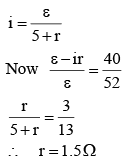Q 1. The current I1 (in A) flowing through 1 Ω resistor in the following circuit is [2020]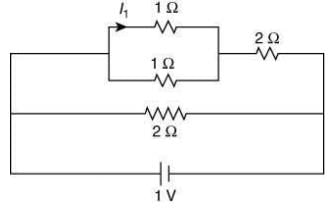
(1) 0.4
(2) 0.5
(3) 0.2
(4) 0.25
Ans: (3)
Solution:
We have the following circuit figure
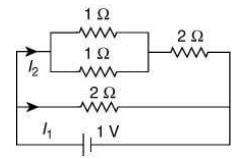
Two 1 Ω resistors are connected is parallel so equivalent resistance is
So, circuit becomes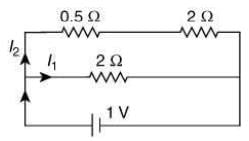
Equivalent resistance of 0.5 Ω and 2 Ω resistor connected in series is
R' = 0.5 + 2 - 2.5 Ω
So, circuit becomes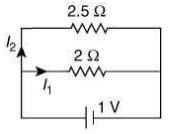
Equivalent resistance of circuit is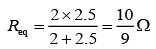
So current in the circuit is
I = V/R = 9/10A
Then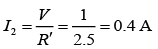
Potential difference across 0.5 Ω resistor is
V' = i2 x R = 0.4 x 0.5 = 0.2 V
So, current through 1 Ω resistor is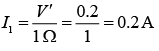
Q 2. In a building there are 15 bulbs of 45 W, 15 bulbs of 100 W, 15 small fans of 10 W and 2 heaters of 1 kW. The voltage of electric mains is 220 V. The minimum fuse capacity (rated value) of the building will be [2020]
(1) 10 A
(2) 25 A
(3) 15 A
(4) 20 A
Ans: (4)
Solution:
Given that, 15 bulbs of 45 W, 15 bulbs of 100 W, 15 small fans of 10 W, 2 heaters of 1 kW = 1000 W, Voltage of electric main, V = 220 V
Total power is given by
P = (15 × 45) + (15 × 100) + (15 × 10) + (2 × 1000)
= 675 + 1500 + 150 + 2000 = 4325 W
We know that,
I = P/V = 4325/220 = 19.659 ∼ 20A
so minimum fuse capacity of the building will be 20 A.
Q 3. The balancing length for a cell is 560 cm in a potentiometer experiment. When an external resistance of 10 Ω is connected in parallel to the cell, the balancing length changes by 60 cm. If the internal resistance of the cell is ( N/10) Ω, where N is an integer then value of N is ________. [2020]
Ans: 12
Solution:
balancing length, L = 560 cm
external resistance, R = 10 Ω
New balancing length after external resistance is connected, L' = 60 cm
Internal resistance of the cell, r = N/10Ω
Let emf of cell be E, and potential difference be V
Then, E = 560 V ...(1)
when external resistance connected in parallel, new emf is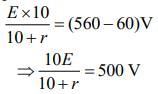
From Eq. (1), we have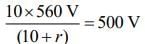
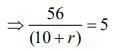
⇒ 56= 5(10 + r)
⇒ 56 = 50+5r
⇒ 5r = 6 ⇒ r = 1.2 Ω
we have,
r = N/10
⇒ 1.2 = N/10
⇒ N = 12
So value of integer N is 12.
Q 4. The length of a potentiometer wire is 1200 cm and it carries a current of 60 mA. For a cell of emf 5 V and internal resistance of 20 Ω, the null point on it is found to be at 1000 cm. The resistance of whole wire is [2020]
(1) 80 Ω
(2) 120 Ω
(3) 60 Ω
(4) 100 Ω
Ans: (4)
Solution:
Given that L = 1200 cm, I = 60mA, ε = 5V, r = 20Ω, l = 1000 cm
We know that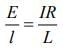
So,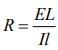
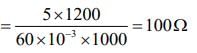
Q 5. Four resistances of 15 Ω, 12 Ω, 4 Ω and 10 Ω respectively are connected in cyclic order to form Wheatstone’s network. The resistance that is to be connected in parallel with the resistance of 10 Ω to balance the network is ___________ Ω. [2020]
Ans: 10
Solution:
Given that P' = 15Ω, Q' = 12Ω, R' = 4Ω, S' = 10Ω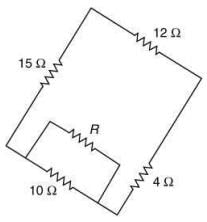
Condition for balanced Wheatstone bridge is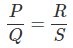
⇒ PS = QR
So,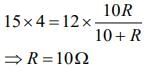
Q 6. The series combination of two batteries, both of the same emf 10 V, but different internal resistance of 20 Ω and 5 Ω, is connected to the parallel combination of two resistors 30 Ω and R Ω. The voltage difference across the battery of internal resistance 20 Ω is zero, the value of R (in Ω) is _______. [2020]
Ans: (30)
Solution:
Given condition can be shown by the following circuit figure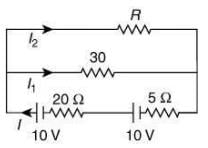
Given that
E1 = E2 = 10V, r1 = 20Ω, r2 = 5Ω, R' = 30Ω, V1 = 0V
We have
V1 = E1 - lr1
⇒ 0 = 10 - 20l
⇒ I = 0.5A
V2 = E2 - lr2
= 10 - (0.5 x 5) = 7.5 a
I = I1 + I2 = 0.5 A ..(1)
V = V1 + V2 = 7.5 V ..(2)
From Eqs. (1) and (2), we have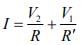
Q 7. In the given circuit diagram, a wire is joining points B and D. The current in this wire is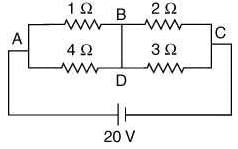 [2020]
[2020]
(1) 0.4 A
(2) 2 A
(3) 4 A
(4) zero
Ans: (2)
Solution:
Total current in the circuit is given by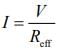
Effective resistance of the combination is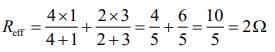
Given that V = 20 V. So,
I = 20/2 = 10 A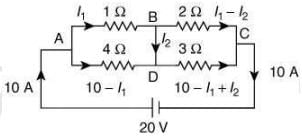
Applying KVL in loop 1, we get
I x I1 - [4 x (10 - I1)] = 0
⇒ 5I1 = 40 ⇒ I1 = 8A
Applying KVL in loop 2, we get
[ 2 x (l1 - l2)] - [3 x (10 - I1 + I2)] = 0
⇒ 5l1 - 5l2 = 30 ⇒ I2 = 2A
Q 8. In a meter bridge experiment, S is a standard resistance. R is a resistance wire. It is found that balancing length is l = 25 cm. If R is replaced by a wire of half length and half diameter that of R of same material, then the balancing distance l' (in cm) will now be _________. [2020]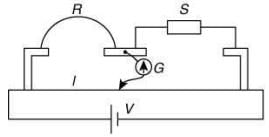
Ans: 40
Solution:
When meter bridge is balanced, we have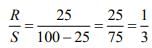
Now,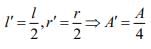
So, new resistance is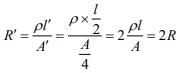
So, new balanced point is
Q 9. A resistance is shown in the figure. Its value and tolerance are given, respectively, by [2019]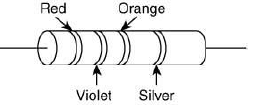
(1) 270 Ω, 10%
(2) 27 kΩ, 10%
(3) 27 kΩ, 20%
(4) 270 Ω, 5%
Ans: (2)
Solution:
This resistor, read from left to right, has the colored bands of RED, VIOLET, ORANGE and SILVER.
The resistance is,
R = (1st Digit × 10 + 2nd Digit) × Multiplier
R = (RED × 10 + VIOLET) × ORANGE = (2 × 10 + 7) × 1,000
= 27,000 Ω = 27 kΩ
Since, the last band is silver, the tolerance is 10%.
Q 10. Drift speed of electrons, when 1.5 A of current flows in a copper wire of cross section 5 mm2, is v. If the electron density in copper is 9 × 1028/m3 the value of v in m/s is close to (take charge of electron to be 1.6 × 10−19 C) [2019]
(1) 0.02
(2) 3
(3) 2
(4) 0.2
Ans: (1)
Solution: Cross section of copper wire, A = 5 mm2 = 5 × 10−6 m2
Current flows in a copper wire, I = 1.5 A
Charge, q = 1.6 × 10−19 C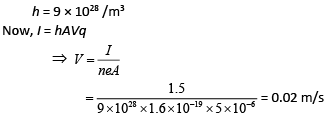
Q 11. A copper wire is stretched to make it 0.5% longer. The percentage change in its electrical resistance if its volume remains unchanged is [2019]
(1) 2.2%
(2) 2.5%
(3) 1.0%
(4) 0.5%
Ans: (3)
Solution: Resistance is given by,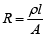
We know that,
Al = Volume (constant)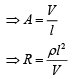
Now, percentage change is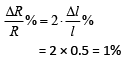
Q 12. When the switch S, in the circuit shown, is closed, then the value of current i will be [2019]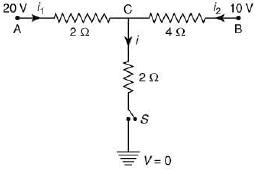
(1) 3 A
(2) 5 A
(3) 4 A
(4) 2 A
Ans: (2)
Solution:
Let V be the voltage at C.
According to the Kirchhoff’s current law, we have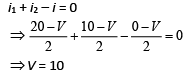

Q 13. A carbon resistance has a following colour code. What is the value of the resistance? [2019]
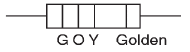
(1) 530 kΩ ± 5%
(2) 5.3 MΩ ± 5%
(3) 6.4 MΩ ± 5%
(4) 64 kΩ ± 10%
Ans: (1)
Solution: Resistor code for Green = 5
Resistor code for Orange = 3
Resistor code for Yellow = 104
Tolerance for Golden = ±5%
Therefore, G O Y Golden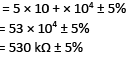
Q 14. In the given circuit the internal resistance of the 18 V cell is negligible. If R1 = 400 Ω, R3 = 100 Ω and R4 = 500 Ω and the reading of an ideal voltmeter across R4 is 5 V, then the value of R2 will be [2019]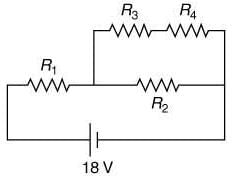
(1) 300 Ω
(2) 450 Ω
(3) 550 Ω
(4) 230 Ω
Ans: (1)
Solution: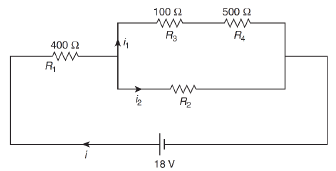
The voltage across resistance R4 is
V4 = 5V
Thus, current i1 = 5/500 = 0.01 A
Voltage across resistance R3 is V3 = 0.01 × 100 = 1 V
Thus, Total voltage = V1 + V3 + V4
(since voltage across R2 is same as voltage across R3 and R4)
⇒ 18 = 1 + 5 + V1
⇒ V1 = 12 V
⇒ i = 12/400 = 0.03 A
⇒ i2 = i – i1 = 0.03 – 0.01 = 0.02 A
therefore,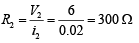
Q 15. A potentiometer wire AB having length L and resistance 12 r is joined to a cell D of emf ε and internal resistance r. A cell C having emf ε/2 and internal resistance 3r is connected. The length AJ at which the galvanometer as shown in figure, for which galvanometer shows no deflection is [2019]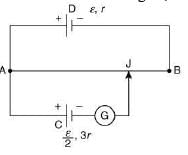
Ans: (3)
Solution:
Let at x distance it will show no deflection then current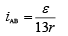
In case of no deflection 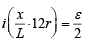
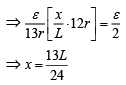
Q 16. A uniform metallic wire has a resistance of 18 Ω and is bent into an equilateral triangle. Then, the resistance between any two vertices of the triangle is [2019]
(1) 4 Ω
(2) 8 Ω
(3) 12 Ω
(4) 2 Ω
Ans: (1)
Solution: Given resistance of metallic wire = 18 Ω
It is bent into an equilateral triangle and the length of each side is same.
And its resistance = 6 Ω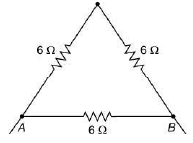
Now, Req between any two vertex is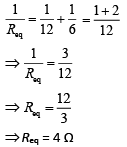
Q 17. In the given circuit the cells have zero internal resistance. The currents (in Amperes) passing through resistance R1 and R2, respectively, are [2019]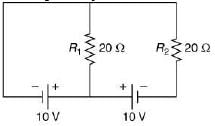
(1) 1, 2
(2) 2, 2
(3) 0.5, 0
(4) 0, 1
Ans: (3)
Solution:
Potential difference across R1 = 10 – 0 = 10 V
Current i through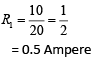
Potential difference across R2 = (0 – 0)Volt
Therefore, current i through R2 = 0
Q 18. A 2W carbon resistor is color coded with green, black, red and brown, respectively. The maximum current which can be passed through this resistor is [2019]
(1) 20 mA
(2) 100 mA
(3) 0.4 mA
(4) 63 mA
Ans: (1)
Solution:
Resistor from color coding
R = 50 × 102 Ω = 5000 Ω
Power = 2 W Power is P = i2R
⇒ 2 = i2 × 5000
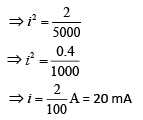
Q 19. The Wheatstone bridge shown in figure here, gets balanced when the carbon resistor used as R1 has the color code (orange, red, brown). The resistors R2 and R4 are 80 Ω and 40 Ω, respectively. Assuming that the color code for the carbon resistors gives their accurate values, the colour code for the carbon resistor, used as R3, would be [2019]
(1) Brow n, Blue, Brown
(2) Brown, Blue, Black
(3) Red, Green, Brown
(4) Grey, Black, Brown
Ans: (1)
Solution: Color code of Orange = 3
Color code of Red = 2
Color code of Brown = 10
So, R1 = 32 × 10 = 320 Ω
The balanced condition of wheat stone bridge is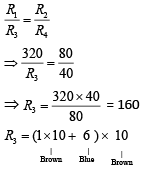
Hence, the color code is Brown, Blue, Brown.
Q 20. The actual value of resistance R, shown in the figure is 30 Ω. This is measured in an experiment as shown using the standard formula R = V/I, where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5% less, then the internal resistance of the voltmeter is [2019]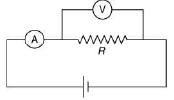
(1) 600 Ω
(2) 570 Ω
(3) 35 Ω
(4) 350 Ω
Ans: (2)
Solution: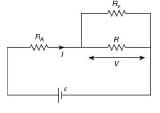
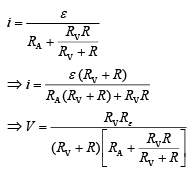
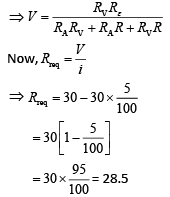
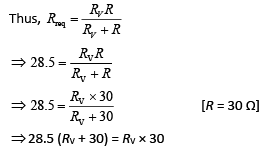
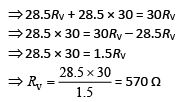
Q 21. A current of 2 mA was passed through an unknown resistor which dissipated a power of 4.4 W. Dissipated power when an ideal power supply of 11 V is connected across it is [2019]
(1) 11 × 10−5 W
(2) 11 × 10−3 W
(3) 11 × 10−4 W
(4) 11 × 105 W
Ans: (1)
Solution: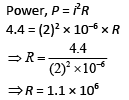
Now, dissipated power is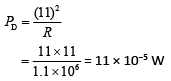
Q 22. In a Wheatstone bridge (see the figure), resistances P and Q are approximately equal. When R = 400 Ω, the bridge is balanced. On interchanging P and Q, the value of R, for balance is 405 Ω. The value of X is close to [2019]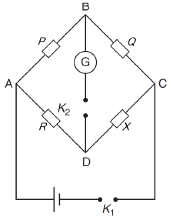
(1) 401.5 Ω
(2) 404.5 Ω
(3) 403.5 Ω
(4) 402.5 Ω
Ans: (4)
Solution:
Balanced condition of Wheatstone bridge is,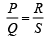
Now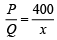 (1)
(1)
Ans,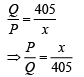 (2)
(2)
From Eq. (1) and Eq. (2), we get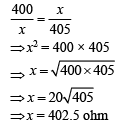
Q 23. Two equal resistances when connected in series to a battery, consume electric power of 60 W. If these resistances are now connected in parallel combination to the same battery, the electric power consumed will be [2019]
(1) 30 W
(2) 60 W
(3) 120 W
(4) 240 W
Ans: (4)
Solution: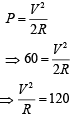
In parallel condition, power consumed is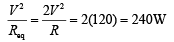
Q 24. The resistance of the meter bridge AB in given figure is 4 Ω. With a cell of emf ε = 0.5 V and rheostat resistance Rh = 2 Ω, the null point is obtained at some point J. When the cell is replaced by another one of emf ε = ε2, the same null point J is found for Rh = 6 Ω. The emf ε2 is [2019]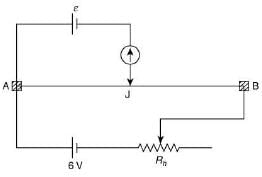
(1) 0.3 V
(2) 0.5 V
(3) 0.6 V
(4) 0.4 V
Ans: (1)
Solution:
Let null point J be at l cm from A.
Then at balance condition we have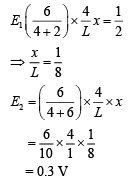
Q 25. In the experimental set up of meter bridge shown in the figure, the null point is obtained at a distance of 40 cm from A. If a 10 Ω resistor is connected in series with R1, the null point shifts by 10 cm. The resistance that should be connected in parallel with (R1 + 10) Ω such that the null point shifts back to its initial position is [2019]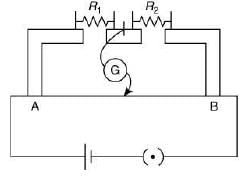
(1) 20 Ω
(2) 40 Ω
(3) 60 Ω
(4) 30 Ω
Ans: (3)
Solution:
Consider the following circuit,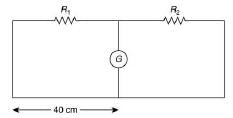
Now using Wheatstone bridge equation, we have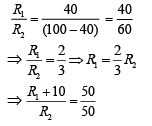
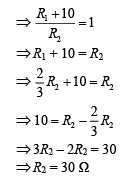
Thus, R1 = 30 – 10 = 20 Ω
Now,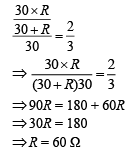
Q 26. In the circuit shown, the potential difference between A and B is [2019]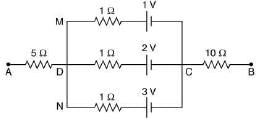
(1) 1 V
(2) 2 V
(3) 3 V
(4) 6 V
Ans:(2)
Solution: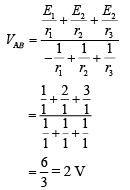
Q 27. An ideal battery of 4 V and resistance R are connected in series in the primary circuit of a potentiometer of length 1 m and resistance 5 Ω. The value of R, to give a potential difference of 5 mV across 10 cm of potentiometer wire, is [2019]
(1) 490 Ω
(2) 480 Ω
(3) 395 Ω
(4) 495 Ω
Ans: (3)
Solution:
Let i be the current flowing in the wire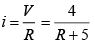
If resistance of 10 m length of wire is r, then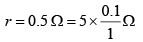
Potential difference, ΔV = ir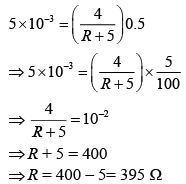
Q 28. In a meter bridge, the wire of length 1 m has a non-uniform cross-section such that, the variation dR/dl of its resistance R with length l is 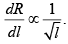 Two equal resistances are connected as shown in the figure. The galvanometer has zero deflection when the jockey is at point P. What is the length AP? [2019]
Two equal resistances are connected as shown in the figure. The galvanometer has zero deflection when the jockey is at point P. What is the length AP? [2019]
(1) 0.2 m
(2) 0.3 m
(3) 0.25 m
(4) 0.35 m
Ans: (3)
Solution: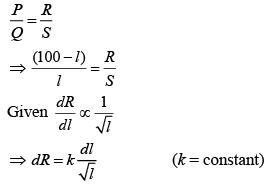
For zero deflection,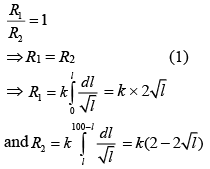
Substitute the value of R1 and R2 in Eq. (1), we have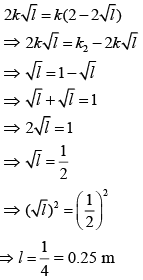
Q 29. Two electric bulbs, rated at (25 W, 220 V) and (100 W, 220 V), are connected in series across a 220 V voltage source. If the 25 W and 100 W bulbs draw powers P1 and P2, respectively, then [2019]
(1) P1 =16 W, P2 = 4 W
(2) P1 = 16 W, P2 = 9 W
(3) P1 = 9 W, P2 = 16 W
(4) P1 = 4 W, P2 = 16 W
Ans: (1)
Solution:
Suppose R1 and R2 are Resistance of bulb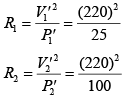
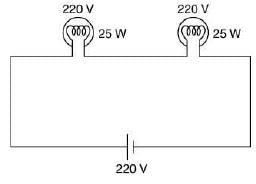
Current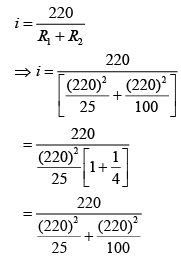
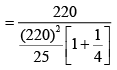
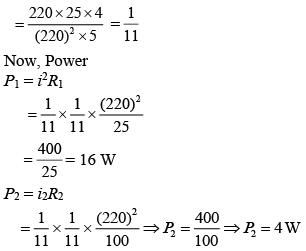
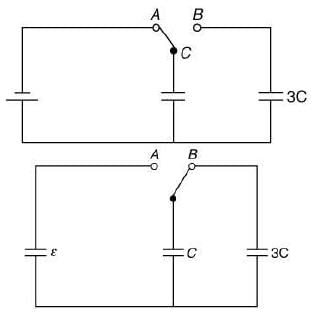
Q 29. In the figure shown, after the switch S is turned from position A to position B, the energy dissipated in the circuit in terms of capacitance C and total charge Q is [2019]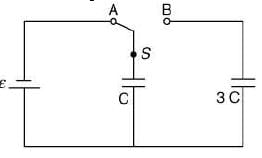
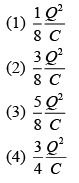
Ans: (2)
Solution:
Change on capacitor C before turning the switch S
Q = CE (1)
Since, when switch S is turned from A to B charge will be transferred from one capacitor to another capacitor until potential will not same.
Let common potential is ε'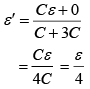
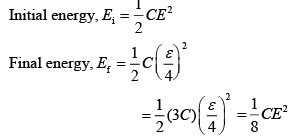
Energy dissipated, E = Ei − Ef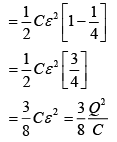
Q 30. In the given circuit diagram, the currents, I1= −0.3 A, I4 = 0.8 A and I5 = 0.4 A, are flowing as shown. The currents I2, I3 and I6, respectively, are [2019]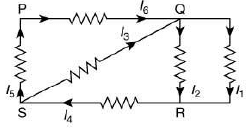
(1) 1.1 A, −0.4 A, 0.4 A
(2) 1.1 A, 0.4 A, 0.4 A
(3) 0.4 A, 1.1 A, 0.4 A
(4) −0.4 A, 0.4 A, 1.1 A
Ans: (2)
Solution:
From using KCL at point S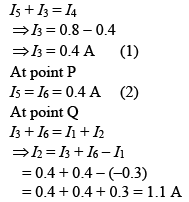
Q 31. Two batteries with e.m.f. 12 V and 13 V are connected in parallel across a load resistor of 10Ω. The internal resistances of the two batteries are 1Ω and 2Ω respectively. The voltage across the load lies between: [2018]
(1) 11.6 V and 11.7 V
(2) 11.5 V and 11.6 V
(3) 11.4 V and 11.5 V
(4) 11.7 V and 11.8 V
Ans: (2)
Solution:
The circuit may be drawn as shown in the figure.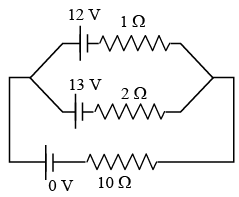
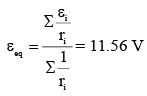
Q 32. In a potentiometer experiment, it is found that no current passes through the galvanometer when the terminals of the cell are connected across 52 cm of the potentiometer wire. If the cell is shunted by a resistance of 5Ω, a balance is found when the cell is connected across 40 cm of the wire. Find the internal resistance of the cell. [2018]
(1) 1Ω
(2) 1.5Ω
(3) 2Ω
(4) 2.5Ω
Ans: (2)
Solution:
When the cell is shunted by a resistance of 5 Ω