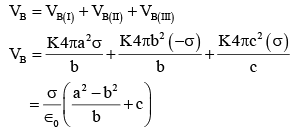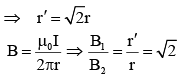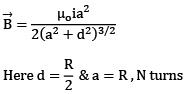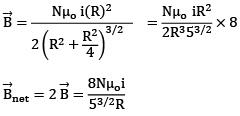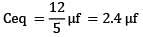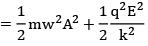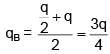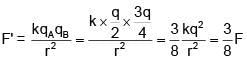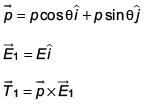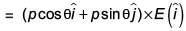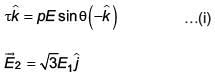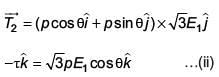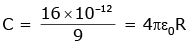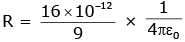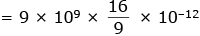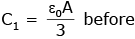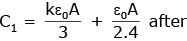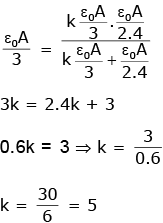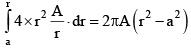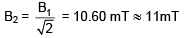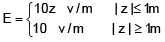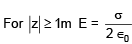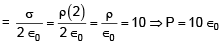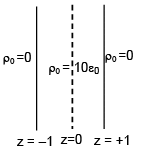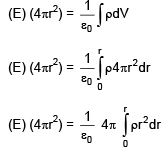Q.84. The charge on a capacitor plate in a circuit, as a function of time, is shown in the figure [2019]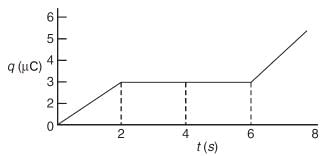 What is the value of current at t = 4 s?
What is the value of current at t = 4 s?
(a) zero
(b) 3 μA
(c) 2 μA
(d) 1.5 μA
Ans. (a)
Slope of q-t graph gives current
I = dq/dt
At t = 4 s, slope is zero
Hence, current at 4 s will be zero.
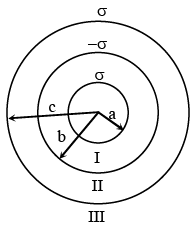
Q.85. Three concentric metal shells A, B and C of respective radii a, b and c (a < b < c) have surface charge densities +σ, -σ and +σ respectively. The potential of shell B is: [2018]
(a) 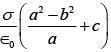
(b) 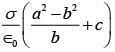
(c) 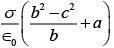
(d) 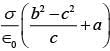
Ans. (b)
Q.86. A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material constant K = 5/3 is inserted between the plates, the magnitude of the induced charge will be: [2018]
(a) 1.2 n C
(b) 0.3 n C
(c) 2.4 n C
(d) 0.9 n C
Ans. (a)
Q = KCV
Qinduced = Q(1-1/K)
⇒ Qinduced = 1.2 nC
Q.87. The dipole moment of a circular loop carrying a current I, is 'm' and the magnetic field at the centre of the loop is B1. When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2. The ratio B1/B2 is: [2018]
(a) 1/√2
(b) √3
(c) √2
(d) 1/√2
Ans. (c)
m = I x πr2
2m = I x π(r')2
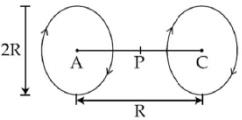
Q.88. A Helmholtz coil has a pair of loops, each with N turns and radius R. They are placed coaxially at distance R and the same current I flows through the loops in the same direction. The magnitude of magnetic field at P, midway between the centres A and C, is given by [Refer to figure given below]: [2018]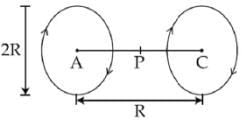 (a)
(a) 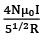
(b) 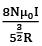
(c) 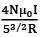
(d) 
Ans. (b)
Q.89. A charge Q is placed at a distance a/2 above the centre of the square surface of edge a as shown in the figure [2018]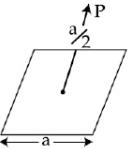 The electric flux through the square surface is:
The electric flux through the square surface is:
(a) Q/6∈o
(b) Q/∈o
(c) Q/3∈o
(d) Q/2∈o
Ans. (a)
Through whole cube = Q/∈o
Through one face = Q/6∈o
Q.90. The equivalent capacitance between A and B in the circuit given below, is: [2018] (a) 5.4 µF
(a) 5.4 µF
(b) 2.4 µF
(c) 3.6 µF
(d) 4.9 µF
Ans. (b)
Q.91. A body of mass M and charge q is connected to a spring of spring constant k. It is oscillating along x direction about its equilibrium position, taken to be at x = 0, with an amplitude A. An electric field E is applied along the x-direction. Which of the following statements is correct? [2018]
(a) The new equilibrium position is at a distance 2qE/K from x = 0
(b) The new equilibrium position is at a distance qE/2K from x = 0
(c) The total energy of the system is 1/2 mω2A2 − 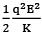
(d) The total energy of the system is 1/2 mω2A2 + 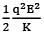
Ans. (d)
Energy at the extreme
= 1/2 kA2 = T. E
After switching on electric field
New mean position ⟹ kxo = qE
xo = qE/k
So entreme position also shifts by qE/k
Q.92. Two identical conducting spheres A and B carry equal charge. They are separated by a distance much larger than their diameters and the force between them is F. A third identical conducting sphere C is uncharged. Sphere C is first touched to A then to B and then removed. As a result the force between A and B would be equal to: [2018]
(a) 3F/4
(b) F/2
(c) 3F/8
(d) F
Ans. (c)
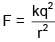
when A and C are touched charge on both will be q/2
Then when B and C are touched
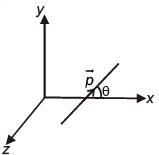
Q.93. An electric dipole has a fixed dipole moment 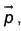 which makes angle θ with respect to x-axis. When subjected to an electric field
which makes angle θ with respect to x-axis. When subjected to an electric field 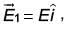 it experiences a torque
it experiences a torque 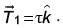 When subjected to another electric field
When subjected to another electric field 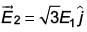 it experiences a torque
it experiences a torque 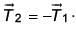 The angle θ is [2017]
The angle θ is [2017]
(a) 60°
(b) 90°
(c) 30°
(d) 45°
Ans. (a)
From (i) and (ii)
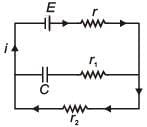
Q.94. In the given circuit diagram when the current reaches steady state in the circuit, the charge on the capacitor of capacitance C will be : [2017]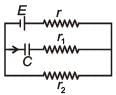 (a)
(a)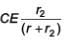
(b)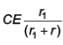
(c) CE
(d)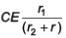
Ans. (a)
In steady state, flow of current through capacitor will be zero.
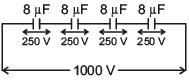
Q.95. A capacitance of 2 μF is required in an electrical circuit across a potential difference of 1.0 kV. A large number of 1 μF capacitors are available which can withstand a potential difference of not more than 300 V.
The minimum number of capacitors required to achieve this is [2017]
(a) 24
(b) 32
(c) 2
(d) 16
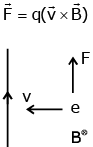
Ans. (b)
Following arrangement will do the needful:
8 capacitors of 1μF in parallel with four such branches in series.
Q.96. A magentic dipole in a constant magnetic field has - [2017]
(a) Maximum potential energy when the torque is maximum
(b) Zero potential energy when the torque is maximum
(c) Zero potential energy when the torque is minimum
(d) Minimum potential energy when the torque is maximum
Ans. (b)
PE = – PE cos θ
τ = PE sin θ
τmax when q = 90°
PE = 0
Q.97. The energy stored in the electric field produced by a metal sphere is 4.5 J. If the sphere contains 4mC charge, its radius will be: [2017]
(a) 32 mm
(b) 16 mm
(c) 28 mm
(d) 20 mm
Ans. (b)
Energy of sphere = Q2/2C
= 16 × 10–3 = 16 mm
Q.98. There is a uniform electrostatic field in a region. The potential at various points on a small sphere centred at P in the region, is found to vary between limits 589.0V to 589.8 V. What is the potential at a point on the sphere whose radius vector makes an angle of 60° with the direction of the field ? [2017]
(a) 589.4 V
(b) 589.5 V
(c) 589.2 V
(d) 589.6 V
Ans. (a)
1 DV = E.d
0.8 = Ed (max)
DV = Edcosθ = 0.8 × cos 60
= 0.4
∴ V= 589.4V
Q.99. Four closed surfaces and corresponding charge distributions are shown below -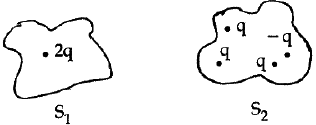
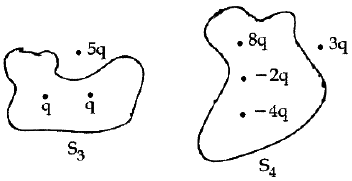 Let the respective electric fluxes through the surfaces be Φ1, Φ2, Φ3 and Φ4. Then - [2017]
Let the respective electric fluxes through the surfaces be Φ1, Φ2, Φ3 and Φ4. Then - [2017]
(a) Φ1 > Φ2 > Φ3 > Φ4
(b) Φ1 < Φ2 = Φ3 > Φ4
(c) Φ1 > Φ3 ; Φ2 > Φ4
(d) Φ1 = Φ2 = Φ3 = Φ4
Ans. (d)
Eq = same in all Φ = Same
Q.100. A negative test charge is moving near a long straight wire carrying a current. The force acting on the test charge is parallel to the direction of the current. The motion of the charge is - [2017]
(a) Away from the wire
(b) Towards the wire
(c) Parallel to the wire along the current
(d) Parallel to the wire opposite to the current
Ans. (b)
Q.101. A combination of parallel plate capacitors is maintained at a certain potential difference. When a 3 mm thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between the plates is increased by 2.4 mm. Find the dielectric constant of the slab. [2017]
When a 3 mm thick slab is introduced between all the plates, in order to maintain the same potential difference, the distance between the plates is increased by 2.4 mm. Find the dielectric constant of the slab. [2017]
(a) 6
(b) 4
(c) 3
(d) 5
Ans. (d)
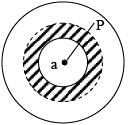
Q.102. The region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density ρ = A/r, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is: [2016]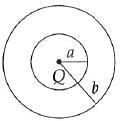
(a)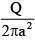
(b)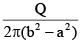
(c)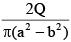
(d)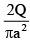
Ans. (a)
Charge in the shaded region =
Total field at P =
For field to be independent of r : Q = 2πAa2
Q.103. A magnetic dipole is acted upon by two magnetic fields which are inclined to each other a tan angle of 75°. One of the fields has magnitude of 15mT. The dipole attains stable equilibrium at an angle 30° with this field. The magnitude of the other field (in mT) is close to: [2016]
(a) 11
(b) 1060
(c) 36
(d) 1
Ans. (a)
B1 sin 30° = B2 sin 45°
Q.104. The potential (in volts) of a charge distribution is given by
V(z) = 30 – 5z2 for |z| ≤ 1m
V(z) = 35 – 10 |z| for |z| ≥ 1m
V(z) does not depend on x and y. If this potential is generated by a constant charge per unit volume ρ0, (in units of ε0) which is spread over certain region, then choose the correct statement.
(a) ρ0 = 40 ε0 in the entire region
(b) ρ0 = 20 ε0 in the entire region
(c) ρ0 = 20 ε0 for |z| in ≤ 1 m and ρ0= 0 else where
(d) ρ0 = 10 ε0 for |z| in ≤ 1 m and ρ0= 0 else where
Ans. (d)
if should be for a sheet lying in x–y plane of thickness z = 2m
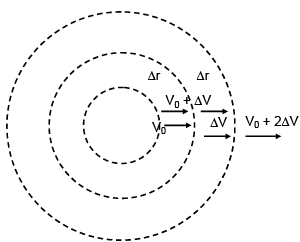
Q.105. Within a spherical charge distribution of charge density ρ(r), N equipotential surfaces of potential V0, V0+ΔV, V0+2ΔV,......, V0+NΔV (ΔV > 0), are drawn and have increasing radii r0,r1,r2,......rN, respectively. If the difference in the radii of the surface is constant for all values of V0 and ΔV then:
(a) ρ(r)αr
(b) 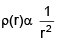
(c) 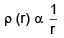
(d) ρ(r) = constant
Ans. (c)
after integral on RHS
We must obtain r2
⇒ ρ ∝ 1/r
FAQs on JEE Main Previous Year Questions (2016-2025): Electrostatics- 2
| 1. What is the formula for electric field due to a point charge? |  |
| 2. How does the electric field inside a conductor vary? |  |
| 3. What is the concept of electric potential? |  |
| 4. How does the electric potential vary with distance from a point charge? |  |
| 5. What is the relation between electric field and electric potential? |  |