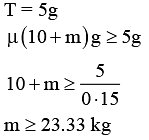Q.1. The maximum vertical height to which a man can throw a ball is 136 m. The maximum horizontal distance upto which he can throw the same ball is: [JEE Mains 2023]
(a) 272 m
(b) 68 m
(c) 192 m
(d) 136 m
Solution:
Correct Answer is Option (a)
Max vertical height
Max horizontal distance
Q.2. Given below are two statements:
Statement I: An elevator can go up or down with uniform speed when its weight is balanced with the tension of its cable.
Statement II: Force exerted by the floor of an elevator on the foot of a person standing on it is more than his/her weight when the elevator goes down with increasing speed.
In the light of the above statements, choose the correct answer from the options given below: [JEE Mains 2023]
(1) Both Statement I and Statement II are true
(2) Statement I is false but Statement II is true
(3) Statement I is true but Statement II is false
(4) Both Statement I and Statement II are false
Solution:
Correct Answer is Option (c)
Statement-1
When force balance it can move with uniform velocity (Uniform speed) True
Statement-2
Elevator going down with increasing speed means its acceleration is downwards mg – N = ma (on person) N = mg – ma (False)
Q.3. As per given figure, a weightless pulley P is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if g = 10 m/s2) [JEE Mains 2023] (a) (4√3 + 1)N
(a) (4√3 + 1)N
(b) 4(√3 + 1)N
(c) (4√3 − 1)N
(d) 4(√3 − 1)N
Solution:
Correct Answer is Option (b)
Q.4. A body of mass 1 kg begins to move under the action of a time dependent force  , where
, where  are the unit vectors along x and y axis. The power developed by above force, at the time t = 2s, will be _________ W. [JEE Mains 2023]
are the unit vectors along x and y axis. The power developed by above force, at the time t = 2s, will be _________ W. [JEE Mains 2023]
Ans. 100
Q.5. Vectors  are perpendicular to each other when 3a + 2b = 7, the ratio of b is x/2 The value of x is [JEE Mains 2023]
are perpendicular to each other when 3a + 2b = 7, the ratio of b is x/2 The value of x is [JEE Mains 2023]
Ans. 1
Q.6. If two vectors  are perpendicular to each other. Then, the value of m will be: [JEE Mains 2023]
are perpendicular to each other. Then, the value of m will be: [JEE Mains 2023]
(1) −1
(2) 3
(3) 2
(4) 1
Ans. (3)
4 × 1 + 2mx – 2 + m2 = 0
m2 – 4m + 4 = 0
(m – 2)2 = 0
m = 2
Q.7. Two bodies of masses m1= 5 kg and m2 = 3 kg are connected by a light string going over a smooth light pulley on a smooth inclined plane as shown in the figure. The system is at rest. The force exerted by the inclined plane on the body of mass m1 will be : [Take g = 10 ms−2] [JEE Mains 2022]
 (a) 30N
(a) 30N
(b) 40N
(c) 50N
(d) 60N
Solution:
Correct Answer is Option (b)
Force on equilibrium, m2g = m1gsinθ ----- (i)
Normal force on m1,
N = m1 gcosθ -----(ii)
From (i) & (ii),
Q.8. A uniform metal chain of mass m and length 'L' passes over a massless and frictionless pulley. It is released from rest with a part of its length 'l' is hanging on one side and rest of its length 'L − l' is hanging on the other side of the pully. At a certain point of time, when l = L / x, the acceleration of the chain is g / 2. The value of x is __________. [JEE Mains 2022]
 (a) 6
(a) 6
(b) 2
(c) 1.5
(d) 4
Solution:
Correct Answer is Option (d)
By solving the above;m2 = 3m1
(L - l) = 3l
L = 4l
l = L / 4 = L/x
Therefore, x = 4
Q.9. The velocity of the bullet becomes one third after it penetrates 4 cm in a wooden block. Assuming that bullet is facing a constant resistance during its motion in the block. The bullet stops completely after travelling at (4 + x) cm inside the block. The value of x is : [JEE Mains 2022]
(a) 2.0
(b) 1.0
(c) 0.5
(d) 1.5
Solution:
Correct Answer is Option (c)
Q.10. A block 'A' takes 2 s to slide down a frictionless incline of 30∘ and length 'l', kept inside a lift going up with uniform velocity 'v'. If the incline is changed to 45∘, the time taken by the block, to slide down the incline, will be approximately : [JEE Mains 2022]
(a) 2.66 s
(b) 0.83 s
(c) 1.68 s
(d) 0.70 s
Solution:
Correct Answer is Option (b)
Q.11. A block of mass M slides down on a rough inclined plane with constant velocity. The angle made by the incline plane with horizontal is θ. The magnitude of the contact force will be : [JEE Mains 2022]
(a) Mg
(b) Mg cosθ
(c) 
(d) 
Solution:
Correct Answer is Option (a)
As the body is moving with constant velocity so forces acting on the body must be balanced.
⇒ Contact force from incline should balance weight of the body.
⇒ | Fcontact | = Mg
Q.12. A bag is gently dropped on a conveyor belt moving at a speed of 2 m/s. The coefficient of friction between the conveyor belt and bag is 0.4. Initially, the bag slips on the belt before it stops due to friction. The distance travelled by the bag on the belt during slipping motion, is : [Take g=10 m/s−2 ] [JEE Mains 2022]
(a) 2 m
(b) 0.5 m
(c) 3.2 m
(d) 0.8 ms
Solution:
Correct Answer is Option (b)
v = 2 m/s
μ = 0.4
a = + (0.4) (g)
= + 4 m/s2
v2 − u2 = 2 as
⇒ (4) = 2 × (4) (s)
s = 0.5 m
Q.13. The area of cross section of the rope used to lift a load by a crane is 2.5×10−4 m2. The maximum lifting capacity of the crane is 10 metric tons. To increase the lifting capacity of the crane to 25 metric tons, the required area of cross section of the rope should be : (take g = 10ms−2 ) [JEE Mains 2022]
(a) 6.25 × 10−4 m2
(b) 10 × 10−4 m2
(c) 1 × 10−4 m2
(d) 1.67 x 10-4m2
Solution:
Correct Answer is Option (a)
Q.14. Two masses M1 and M2 are tied together at the two ends of a light inextensible string that passes over a frictionless pulley. When the mass M2 is twice that of M1, the acceleration of the system is a1. When the mass M2 is thrice that of M1, the acceleration of the system is a2. The ratio a1 / a2 will be : [JEE Mains 2022]
 (a) 1/3
(a) 1/3
(b) 2/3
(c) 3/2
(d) 1/2
Solution:
Correct Answer is Option (b)
= g/3
And,
∴
Q.15. A monkey of mass 50 kg climbs on a rope which can withstand the tension (T) of 350 N. If monkey initially climbs down with an acceleration of 4 m/s2 and then climbs up with an acceleration of 5 m/s2. Choose the correct option (g=10 m/s2). [JEE Mains 2022]
(a) T=700 N while climbing upward
(b) T=350 N while going downward
(c) Rope will break while climbing upward
(d) Rope will break while going downward
Solution:
Correct Answer is Option (c)
F.B.D of monkey while moving downward:Using Newton’s second law
mg – T = ma1
∴ 500 – T = 50 × 4
⇒ T = 300 N
F.B.D of monkey while moving up:
Using Newton’s second law of motion
T – mg = ma2
⇒ T – 500 = 50 × 5
⇒ T = 750 N
Breaking strength of string = 350 N
As T > 350N,
∴ String will break while monkey is moving upward
Q.16. Three masses M = 100 kg, m1 = 10 kg and m2 = 20 kg are arranged in a system as shown in figure. All the surfaces are frictionless and strings are inextensible and weightless. The pulleys are also weightless and frictionless. A force F is applied on the system so that the mass m2 moves upward with an acceleration of 2 ms−2. The value of F is : ( Take g = 10 ms−2 ) [JEE Mains 2022] (a) 3360 N
(a) 3360 N
(b) 3380 N
(c) 3120 N
(d) 3240 N
Solution:
Correct Answer is Option (c)
Let acceleration of 100 kg block = a1
Q.17. For a free body diagram shown in the figure, the four forces are applied in the 'x' and 'y' directions. What additional force must be applied and at what angle with positive x-axis so that the net acceleration of body is zero? [JEE Mains 2022] (a) √2N,45∘
(a) √2N,45∘
(b) √2N,135∘
(c) 2 / √3N,30∘
(d) 2N,45∘
Solution:
Correct Answer is Option (a)
Resultant of already applied forces =
⇒ Force required to balance =
⇒ Force required = √2 N in magnitude at angle 45∘ with +ve x-axis
Q.18. A 2 kg block is pushed against a vertical wall by applying a horizontal force of 50 N. The coefficient of static friction between the block and the wall is 0.5. A force F is also applied on the block vertically upward (as shown in figure). The maximum value of F applied, so that the block does not move upward, will be : (Given : g = 10 ms−2) [JEE Mains 2022] (a)10N
(a)10N
(b) 20N
(c) 25N
(d) 45N
Solution:
Correct Answer is Option (d)
Here Fmax force is trying to move the block upward so friction force will be applied towards downward.
Along horizontal direction,
N = 50 N
Along vertical diretion,
Fmax = mg + fmax
= 2 × 10 + μN
= 20 + 0.5 × 50
= 20 + 25
= 45 N
Q.19. At t = 0, truck, starting from rest, moves in the positive x-direction at uniform acceleration of 5 ms−2. At t = 20 s, a ball is released from the top of the truck. The ball strikes the ground in 1 s after the release. The velocity of the ball, when it strikes the ground, will be : (Given g = 10 ms−2) [JEE Mains 2022]
(a) 
(b) 
(c) 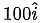
(d) 
Solution:
Correct Answer is Option (a)
At t = 20 s,
velocity of truck,
v = 0 + 5 × 20 = 100 m/sAt 20 sec a ball is dropped from the truck, so velocity of ball will be same as truck.
Velocity of truck at x-direction = 100 m/s and in y-direction = 0.
∴ Velocity of ball vx = 100 m/s, vy = 0
Now ball will show projectile motion where vertically downward acceleration g = 10 m/s act on the ball.
As horizontally no acceleration acting on the ball so horizontal velocity 100 m/s will remain unchanged.
Velocity of the ball when it reach the ground along y-direction after 1 sec.
∴ Velocity of ball
Q.20. A block of mass 10 kg starts sliding on a surface with an initial velocity of 9.8 ms−1. The coefficient of friction between the surface and block is 0.5. The distance covered by the block before coming to rest is : [use g = 9.8 ms−2] [JEE Mains 2022]
(a) 4.9 m
(b) 9.8 m
(c) 12.5 m
(d) 19.6 m
Solution:
Correct Answer is Option (b)
= 9.8 m
Q.21. An object of mass 5 kg is thrown vertically upwards from the ground. The air resistance produces a constant retarding force of 10 N throughout the motion. The ratio of time of ascent to the time of descent will be equal to : [Use g = 10 ms−2]. [JEE Mains 2022]
(a) 1 : 1
(b) √2 : √3
(c) √3 : √2
(d) 2 : 3
Solution:
Correct Answer is Option (b)
Let time taken to ascent is t1 and that to descent is t2. Height will be same so
Q.22. In the arrangement shown in figure a1, a2, a3 and a4 are the accelerations of masses m1, m2, m3 and m4 respectively. Which of the following relation is true for this arrangement? [JEE Mains 2022]
(a) 4a1 + 2a2 + a3 + a4 = 0
(b) a1 + 4a2 + 3a3 + a4 = 0
(c) a1 + 4a2 + 3a3 + 2a4 = 0
(d) 2a1 + 2a2 + 3a3 + a4 = 0
Solution:
Correct Answer is Option (a)
From virtual work done method,
(4T × a1) + (2T × a2) + (T × a3) + (T × a4) = 0
⇒ 4a1 + 2a2 + a3 + a4 = 0
Q.23. A person is standing in an elevator. In which situation, he experiences weight loss? [JEE Mains 2022]
(a) When the elevator moves upward with constant acceleration
(b) When the elevator moves downward with constant acceleration
(c) When the elevator moves upward with uniform velocity
(d) When the elevator moves downward with uniform velocity
Solution:
Correct Answer is Option (b)
N1 = mg
N2 = mg + ma
N3 = mg − ma
N4 = mg
N5 = mg
Q.24. A system of two blocks of masses m = 2 kg and M = 8 kg is placed on a smooth table as shown in figure. The coefficient of static friction between two blocks is 0.5. The maximum horizontal force F that can be applied to the block of mass M so that the blocks move together will be : [JEE Mains 2022] (a) 9.8 N
(a) 9.8 N
(b) 39.2 N
(c) 49 N
(d) 78.4 N
Solution:
Correct Answer is Option (c)
Q.25. A √34 m long ladder weighing 10 kg leans on a frictionless wall. Its feet rest on the floor 3 m away from the wall as shown in the figure. If Ef and Fw are the reaction forces of the floor and the wall, then ratio of Fw/Ff will be : (Use g = 10 m/s2.) [JEE Mains 2022] (a) 6 / √100
(a) 6 / √100
(b) 3 / √113
(c) 3 / √109
(d) 2 / √109
Solution:
Correct Answer is Option (c)
Taking torque from B
Fw × 5 = 32mg
⇒ Fw = 310 × 10 × 10
= 30N
N = mg = 100N
and fr = Fw = 30N
so
so
Q.26. A block of mass 2 kg moving on a horizontal surface with speed of 4 ms−1 enters a rough surface ranging from x = 0.5 m to x = 1.5 m. The retarding force in this range of rough surface is related to distance by F = −kx where k = 12 Nm−1. The speed of the block as it just crosses the rough surface will be : [JEE Mains 2022]
(a) zero
(b) 1.5 ms−1
(c) 2.0 ms−1
(d) 2.5 ms−1
Solution:
Correct Answer is Option (c)
F = -12x
v = 2 m/sec
Q.27. A block of mass M placed inside a box descends vertically with acceleration 'a'. The block exerts a force equal to one-fourth of its weight on the floor of the box. The value of 'a' will be [JEE Mains 2022]
(a) g / 4
(b) g / 2
(c) 3g / 4
(d) g
Solution:
Correct Answer is Option (c)
Using Newton's second law
mg − mg / 4 = ma
⇒ a = 3g / 4
Q.28. A block of mass 40 kg slides over a surface, when a mass of 4 kg is suspended through an inextensible massless string passing over frictionless pulley as shown below. The coefficient of kinetic friction between the surface and block is 0.02. The acceleration of block is. (Given g = 10 ms−2.) [JEE Mains 2022] (a) 1 ms−2
(a) 1 ms−2
(b) 1/5 ms−2
(c) 4/5 ms−2
(d) 8/11 ms−2
Solution:
Correct Answer is Option (c)
frmax = μN
=0.02 × 400
= 8 N
Let the acceleration is a as shown then.
40 − T = 4a
T − 8 = 40a
⇒ a = 32/44 = 8/11 m/s2
Q.29. A body of mass M at rest explodes into three pieces, in the ratio of masses 1 : 1 : 2. Two smaller pieces fly off perpendicular to each other with velocities of 30 ms−1 and 40 ms−1 respectively. The velocity of the third piece will be : [JEE Mains 2022]
(a) 515 ms−1
(b) 25 ms−1
(c) 35 ms−1
(d) 50 ms−1
Solution:
Correct Answer is Option (b)
Conserving momentum :
Q.30. A block of mass m slides along a floor while a force of magnitude θ is applied to it at an angle F as shown in figure. The coefficient of kinetic friction is μκ. Then, the block's acceleration 'a' is given by : (g is acceleration due to gravity) [2021 6 March (Shift 1)] (a)
(a) 
(b) 
(c) 
(d) 
Solution:
Correct Answer is Option (b)
N = mg − f sin θ
F cos θ − μkN = ma
F cos θ − μk(mg − F sin θ) = ma
Q.31. A block of 200g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20cm. If the block takes 40s to complete one round, the normal force by the side walls of the groove is : [2021 16 March (Shift 1)]
(a) 0.0314 N
(b) 9.859 × 10−2 N
(c) 6.28 × 10−3 N
(d) 9.859 × 10−4 N
Solution:
Correct Answer is Option (d)
N = mω2R
Given m = 0.2 kg, T = 40 S, R = 0.2 m
Put values in equation (1)
N = 9.859 × 10−4 N
Q.32. Consider a frame that is made up of two thin massless rods A and B as shown in the figure. A vertical force  of magnitude 100N is applied at point A of the frame.
of magnitude 100N is applied at point A of the frame. Suppose the force is
Suppose the force is  resolved parallel to the arms AB and AC of the frame. The magnitude of the resolved component along the arm AC is xN. The value of x, to the nearest integer, is ____ .
resolved parallel to the arms AB and AC of the frame. The magnitude of the resolved component along the arm AC is xN. The value of x, to the nearest integer, is ____ .
[Given: sin(35º) = 0.573, cos(35º) = 0.819
sin(110º) = 0.939, cos(110º) = -0.342] [2021 16 March (Shift 1)]
Solution: 82N
Component along AC
= 100 cos 35∘N
= 100 × 0.819 N
= 81.9 N
≈ 82 N
Q.33. Statement I: A cyclist is moving on an unbanked road with a speed of 7kmh-1 and takes a sharp circular turn along a path of radius of 2 m without reducing the speed. The static friction coefficient is 0.2 . The cyclist will not slip and pass the curve (g = 9.8 m/s2)
Statement II: If the road is banked at an angle of 45°, cyclist can cross the curve of 2 m radius with the speed of 18.5kmh-1 without slipping.
In the light of the above statements, choose the correct answer from the options given below. [2021 16 March (Shift 2)]
(a) Statement I is incorrect and statement II is correct
(b) Statement I is correct and statement II is incorrect
(c) Both statement I and statement II are false
(d) Both statement I and statement II are true
Solution:
Correct Answer is Option (d)
Statement I:
Vmax = 1-97 m/s
7 km/h = 1.944 m/s
Speed is lower than vmax, hence it can take safe turn.
Statement II:
18.5 km/h = 5.14 m/s
Speed is lower than vmax, hence it can take safe turn.
Q.34. A body of mass 2 kg moves under a force of  . It starts from rest and was at the origin initially. After 4 s, its new coordinates are (8, b, 20). The value of b is_____. (Round off to the Nearest Integer) [2021 16 March (Shift 2)]
. It starts from rest and was at the origin initially. After 4 s, its new coordinates are (8, b, 20). The value of b is_____. (Round off to the Nearest Integer) [2021 16 March (Shift 2)]
Solution: 12
Q.35. A modem grand-prix racing car of mass m is travelling on a flat track in a circular arc of radius R with a speed v. If the coefficient of static friction between the tyres and the track is μs, then the magnitude of negative lift FL acting downwards on the car is : (Assume forces on the four tyres are identical and g = acceleration due to gravity) [2021 17 March (Shift 1)]
(a) 
(b) 
(c) 
(d) 
Solution:
Correct Answer is Option (b)
Q.36. Two blocks (m = 0.5 kg and M = 4.5 kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is 3/7. Then the maximum horizontal force that can be applied on the larger block so that the blocks move together is_____N. (Round off to the Nearestlnteger)
[Take g as 9.8 ms-2 ] [2021 17 March (Shift 1)]
Solution: 21
Q.37. A body of mass 1 kg rests on a horizontal floor with which it has a coefficient of static friction 1/√3. It is desired to make the body move by applying the minimum possible force FN. The value of F will be ______(Round off to the Nearest Integer)
[Take g = 10 ms-2] [2021 17 March (Shift 2)]
Solution: 5
Q.38. A boy of mass 4 kg is standing on a piece of wood having mass 5 kg. If the coefficient of friction between the wood and the floor is 0.5, the maximum force that the boy can exert on the rope so that the piece of wood does not move from its place is N.(Round off to the Nearest Integer) [Take g = 10 ms-2] [2021 17 March (Shift 2)]
Solution: 30
N + T = 90
T = μN = 0.5(90 − T)
1.5 T = 45
T = 30
Q.39. A bullet of mass 0.1 kg is fired on a wooden block to pierce through it, but it stops after moving a distance of 50 cm into it. If the velocity of bullet before hitting the wood is 10 m/s and it slows down with uniform deceleration, then the magnitude of effective retarding force on the bullet is 'x' N. The value of x to the nearest integer is ___. [2021 18 March (Shift 1)]
Solution: 10
v2 = u2 + 2as
0 = (10)2 + 2(−a) (1/2)
a = 100 m/s2
F = ma = (0.1)(100) = 10 N
Q.40. A 60 HP electric motor lifts an elevator having a maximum total load capacity of 2000 kg. If the frictional force on the elevator is 4000 N, the speed of the elevator at full load is close to (1 HP = 746 W, g = 10 m/s2 ) [2020]
(a) 1.7 m/s
(b) 1.9 m/s
(c) 1.5 m/s
(d) 2.0 m/s
Solution:
Correct Answer is Option (b)
Given that M = 2000 kg, g = 10 m/s2, f = 4000 N, P = 60 HP = 60 × 746 J
Total force acting on elevator is:
F = Mg + f
= (2000 x 10) + 4000 = 24000 N
Power of electric motor is given by
P = Fv
⇒ v = P/F
Q.41. A mass of 10 kg is suspended by a rope of length 4 m, from the ceiling. A force F is applied horizontally at the mid-point of the rope such that the top half of the rope makes an angle of 45° with the vertical. Then F equals (Take g = 10 m/s2 and the rope to be massless) [2020]
(a) 100 N
(b) 90 N
(c) 70 N
(d) 75 N
Solution:
Correct Answer is Option (a)
Let tension in the string be T
At equilibrium, we have
T sin 450 = F ..(1)
and T cos450 = 10 x g ..(2)
Dividing Eq. (1) by Eq. (2), we get(∵ g = 10 m/s)
⇒ I = F/100
⇒ F = 100 N
Q.42. Consider a uniform cubical box of side 'a' on a rough floor that is to be moved by applying minimum possible force F at a point 'b' above its centre of mass (see figure). If the coefficient of friction is μ = 0.4, the maximum possible value of 100.b/a for box not to topple before moving is ______. [2020]
Solution: 75
Given that μ = 0.4Condition for no topple is
Friction force is given by
F = μmg
So,
So, maximum value of
Therefore,
So, maximum possible value of 100 × b/a = 75.
Q.43. A spring-mass system (mass m, spring constant k and natural length l) rests in equilibrium on a horizontal disc. The free end of the spring is fixed at the centre of the disc. If the disc together with spring-mass system, rotates about its axis with an angular velocity ω, ( k >> mω2) the relative change in the length of the spring is best given by the option [2020]
Solution:
Correct Answer is Option (3)
Let the elongation in length of the spring be Δl.
Forces act on the system are:
(i) Centripetal force, which act outward which help in expansion in spring:
Fc = mω2 (l + Δl)
(ii) Spring restoring force, which act inward which opposed the further expansion in spring.
Fs = kΔl
At balanced point, we have:
The relative change in the length of the spring is:
Since k>> mω2 then
Q.44. A block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6. What should be the minimum value of force P such that the block does not move downward? (Take g = 10 m/s2) [2019] (a) 32 N
(a) 32 N
(b) 18 N
(c) 23 N
(d) 25 N
Solution:
Correct Answer is Option (a)
The coefficient of static friction, μ = 0.6
The resultant force is
P + μmg cos θ = 3 + mg sin θ
Given m = 10 kg, μ = 0.6 and g = 10 m/s2
⇒ P + 0.6 × 50√2 = 3 + 50√2
⇒ P + 42.42 = 73.71
⇒ P = 73.71 - 42.42 = 31.29
Therefore, P ≈ 32 N
Q.45. A mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45° at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g = 10 m/s2). [2019]
(a) 200 N
(b) 140 N
(c) 70 N
(d) 100 N
Solution:
Correct Answer is Option (d)
Q.46. A particle of mass m is moving in a straight line with momentum p. Starting at time t = 0, a force F = kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here, k is a constant. The value of T is [2019]
(a) 
(b) 
(c) 
(d) 
Solution:
Correct Answer is Option (b)
Q.47. A block kept on a rough inclined plane, as shown in the figure, remains at rest up to a maximum force 2 N down the inclined plane. The maximum external force up the inclined plane that does not move the block is 10 N. The coefficient of static friction between the block and the plane is (Take g = 10 m/s2) [2019] (a) √3/2
(a) √3/2
(b) √3/4
(c) 1/2
(d) 2/3
Solution:
Correct Answer is Option (a)
Block is at rest then, 2 N force is applied.
Now, friction is
When 2 N force is applied in downward direction, thus
Block is rest (10 N force is applied)
When 10 N force is applied in upward direction, then
Dividing Eq. (1) by Eq. (2), we get
Q.48. Two masses m1 = 5 kg and m2 = 10 kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weight m that should be put on top of m2 to stop the motion is: [2018] (a) 18.3 g
(a) 18.3 g
(b) 23.3 kg
(c) 43.3 kg
(d) 10.3 kg
Solution:
Correct Answer is Option (b)
Q.49. A given object takes n times more time to slide down a 45° rough inclined plane as it takes to slide down a perfectly smooth 45° incline. The coefficient of kinetic friction between the object and the incline Is: [2018]
(a) 
(b) 
(c) 
(d) 
Solution:
Correct Answer is Option (a)
So
Sin θ = n2 sinθ − µn2 cosθ
⇒ 1 = n2 − µn2
⇒ 1 − n2 = −µn2
⇒ n2 − 1 = −µn2
⇒ µ = 1 − 1/n2
Q.50. A man grows into a giant such that his linear dimensions increase by a factor of 9. Assuming that his density remains the same, the stress in the leg will change by a factor of [2017]
(a) 81
(b) 1/81
(c) 9
(d) 1/9
Solution:
Correct Answer is Option (c)
∵ Density remains same
So, mass ∝ Volume
Q.51. A body is thrown vertically upwards. Which one of the following graphs correctly represent the velocity vs time? [2017]
(a) 
(b) 
(c)
(d)
Solution:
Correct Answer is Option (a)
Acceleration is constant and negative
Q.52. A uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is: [2017] (a)
(a) 
(b) 
(c) 
(d) 
Solution:
Correct Answer is Option (d)
Q.53. A conical pendulum of length 1 m makes an angle q = 45° w.r.t. Z-axis and moves in a circle in the XY plane. The radius of the circle is 0.4 m and its center is vertically below O. The speed of the pendulum, in its circular path, will be (Take g = 10 ms-2) [2017] (a) 0.2 m/s
(a) 0.2 m/s
(b) 0.4 m/s
(c) 2 m/s
(d) 4 m/s
Solution:
Correct Answer is Option (c)
Q.54. The machine as shown has 2 rods of length 1 m connected by a pivot at the top. The end of one rod is connected to the floor by a stationary pivot and the end of the other rod has a roller that rolls along the floor in a slot. As the roller goes back and forth, a 2 kg weight moves up and down. If the roller is moving towards right at a constant speed, the weight moves up with a [2017] (a) Speed which is 3/4th of that of the roller when the weight is 0.4 m above the ground
(a) Speed which is 3/4th of that of the roller when the weight is 0.4 m above the ground
(b) Constant speed
(c) Decreasing speed
(d) Increasing speed
Solution:
Correct Answer is Option (c)
Q.55. A point particle of mass m, moves along the uniformly rough track PQR as shown in the figure. The coefficient of friction, between the particle and the rough track equals m. The particle is released, from rest, from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The values of the coefficient of friction m and the distance x (= QR), are, respectively close to [2016] (a) 0.2 and 6.5 m
(a) 0.2 and 6.5 m
(b) 0.2 and 3.5 m
(c) 0.29 and 3.5 m
(d) 0.29 and 6.5 m
Solution:
Correct Answer is Option (c)
From work energy theorem and given condition:
∴
∴
Q.56. A rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the rocket, making an angle q. With the horizontal, a point object of mass m is kept. The minimum coefficient of friction μmin between the mass and the inclined surface such that the mass does not move is: [2016]
(a) tanθ
(b) tan2θ
(c) 3 tanθ
(d) 2 tanθ
Solution:
Correct Answer is Option (a)
Free body diagram is shown in the figure.
Psuedo force on the object is 2mg in the downward direction as seen from the rocket frame of reference.
Normal force in the direction perpendicular to the inclined plane.
N = 3mg cos(θ)
Maximum frictional force in the direction along the plane,
Fr = μmN cos(θ)
∴ Fr = 3μmmg cos(θ)
This should balance the force on the block along the downward direction of plane.
3mg sin(θ) = 3μmmg cos(θ)
μm = tan(θ)
Q.57. Which of the following option correctly describes the variation of the speed v and acceleration 'a' of a point mass falling vertically in a viscous medium that applies a force F = –kv, where 'k' is constant, on the body ?( Graphs are schematic and not drawn to scale) [2016]



Solution:
Correct Answer is Option (4)
a = g – αv
Q.58. Concrete mixture is made by mixing cement, stone and sand in a rotating cylindrical drum. If the drum rotates too fast, the ingredients remain stuck to the wall of the drum and proper mixing of ingredients does not take place. The maximum rotational speed of the drum in revolutions per minute (rpm) to ensure proper mixing is close to (Take the radius of the drum to be 1.25m and its axle to be horizontal): [2016]
(a) 1.3
(b) 0.4
(c) 27.0
(d) 8.0
Solution:
Correct Answer is Option (c)
For just complete rotation:






















 Here Fmax force is trying to move the block upward so friction force will be applied towards downward.
Here Fmax force is trying to move the block upward so friction force will be applied towards downward. At t = 20 s,
At t = 20 s,



 N1 = mg
N1 = mg
 Taking torque from B
Taking torque from B

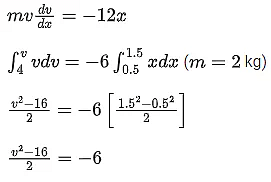

 frmax = μN
frmax = μN














 (∵ g = 10 m/s)
(∵ g = 10 m/s)