Q.1. The velocity time graph of a body moving in a straight line is shown in figure. The ratio of displacement to distance travelled by the body in time 0 to 10 s is : [(JEE Main 2023)]
The ratio of displacement to distance travelled by the body in time 0 to 10 s is : [(JEE Main 2023)]
(a) 1: 1
(b) 1: 2
(c) 1: 3
(d) 1: 4
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Displacement is calculated as the area under the v-t curve. Since, displacement is a vector quantity, negative displacement will be subtracted from the positive displacement.
Displacement = area (v x t)
= (8 × 2) + (4 × 4) – (2 × 4) – (2 × 4)
= 16 + 16 - 8 - 8
= 32 – 16
= 16 m
Distance, on the hand, is a scalar quantity. So we will add the total area under the v-t graph to obtain the total distance.
Distance =
(8 × 2) + (4 × 4) + (2 × 4) + (2 × 4)= 16 + 16 + 8 + 8
= 48 m
The ratio of displacement to distance is 16:48 = 1:3
Q.2. A ball is released from a height h. If t1 and t2 be the time required to complete first half and second half of the distance respectively. Then, choose the correct relation between t1 and t2. [(JEE Main 2022)]
(a) t1 = (√2)t2
(b) t1 = (√2 − 1)t2
(c) t2 = (√2 + 1)t1
(d) t2 = (√2 − 1)t1
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
For first h / 2 distance,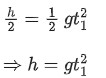
For total distance h,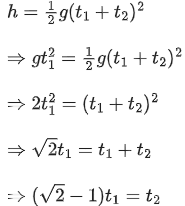
Q.3. A juggler throws balls vertically upwards with same initial velocity in air. When the first ball reaches its highest position, he throws the next ball. Assuming the juggler throws n balls per second, the maximum height the balls can reach is [(JEE Main 2022)]
(a) g/2n
(b) g/n
(c) 2gn
(d) g/2n2
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
The juggler throws n balls per second.
∴ Interval between balls = 1 / n seconds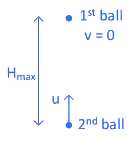
At maximum height velocity of first ball v = 0
Juggler throws all balls with same initial velocity = u
For 1st ball,
u1 =u, v1 = 0, a = −g, S = Hmax
Using formula,
v2 = u2 + 2as
0 = u2 − 2gHmax
⇒ Hmax = u2 / 2g ...... (1)
And using formula,
v = u + at
⇒ 0 = u −gt
⇒ t = u / g
∴ Time taken by ball 1 to reach maximum height (Hmax) = / g
According to the question,
t = 1n
⇒ u / g = 1/ n
⇒ u = g / n ....... (2)
Putting value of u in equation (1), we get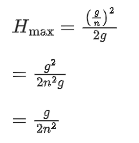
Q.4. If 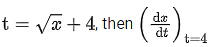 is: [(JEE Main 2022)]
is: [(JEE Main 2022)]
(a) 4
(b) zero
(c) 8
(d) 16
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 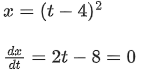
Q.5. A ball is thrown up vertically with a certain velocity so that, it reaches a maximum height h. Find the ratio of the times in which it is at height h / 3 while going up and coming down respectively. [(JEE Main 2022)]
(a) 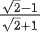
(b) 
(c) 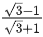
(d) 1/3
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 
Q.6. At time t=0 a particle starts travelling from a height 7 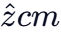 in a plane keeping z coordinate constant. At any instant of time it's position along the
in a plane keeping z coordinate constant. At any instant of time it's position along the 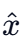 and
and 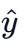 directions are defined as 3t and 5t3 respectively. At t = 1s acceleration of the particle will be [(JEE Main 2022)]
directions are defined as 3t and 5t3 respectively. At t = 1s acceleration of the particle will be [(JEE Main 2022)]
(a) −30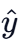
(b) 30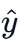
(c) 3 +15
+15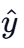
(d) 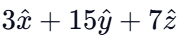
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 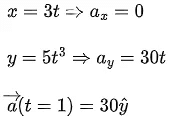
Q.7. A NCC parade is going at a uniform speed of 9 km/h under a mango tree on which a monkey is sitting at a height of 19.6 m. At any particular instant, the monkey drops a mango. A cadet will receive the mango whose distance from the tree at time of drop is: (Given g=9.8 m/s2 ) [(JEE Main 2022)]
(a) 5 m
(b) 10 m
(c) 19.8 m
(d) 24.5 m
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 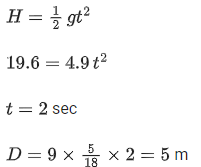
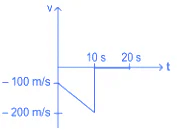
Q.8. A bullet is shot vertically downwards with an initial velocity of 100 m/s from a certain height. Within 10 s, the bullet reaches the ground and instantaneously comes to rest due to the perfectly inelastic collision. The velocity-time curve for total time t = 20 s will be: (Take g = 10 m/s2). [(JEE Main 2022)]
(a)
(b)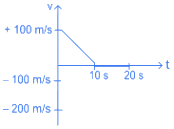
(c)
(d)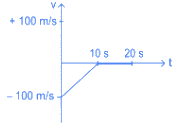
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
|v10| = (100 + 10 × 10) m/s
v10 = −200 m/s and v0 = −100 m/s
from 10s to 20s velocity remains zero
⇒ from t = 0s to 10s velocity increases in magnitude linearly.
⇒ graph given in option A fits correctly.
Q.9. Two projectiles are thrown with same initial velocity making an angle of 45∘ and 30∘ with the horizontal respectively. The ratio of their respective ranges will be : [(JEE Main 2022)]
(a) 1 : √2
(b) √2 : 1
(c) 2 : √3
(d) √3 : 2
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 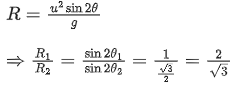
Q.10. Two projectiles thrown at 30∘ and 45∘ with the horizontal respectively, reach the maximum height in same time. The ratio of their initial velocities is : [(JEE Main 2022)]
(a) 1:2
(b) 2:1
(c) 2:1
(d) 1:2
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 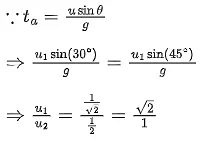
Q.11. A ball is projected from the ground with a speed 15 ms−1 at an angle θ with horizontal so that its range and maximum height are equal, then 'tan θ' will be equal to : [(JEE Main 2022)]
(a) 1 / 4
(b) 1 / 2
(c) 2
(d) 4
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 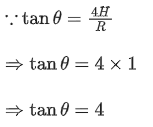
Q.12. Two projectiles P1 and P2 thrown with speed in the ratio √3 : √2, attain the same height during their motion. If P2 is thrown at an angle of 60∘ with the horizontal, the angle of projection of P1 with horizontal will be : [(JEE Main 2022)]
(a) 15∘
(b) 30∘
(c) 45∘
(d) 60∘
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
We know,
Maximum height of a projectile (H) = u2sin2θ / 2g
Given, Ratio of initial velocity of two projectile
u1 / u2 = √3 / √2
Both projectile reach the same maximum height.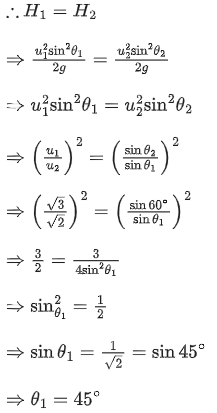
Q.13. A projectile is projected with velocity of 25 m/s at an angle θ with the horizontal. After t seconds its inclination with horizontal becomes zero. If R represents horizontal range of the projectile, the value of θ will be :[use g = 10 m/s2] [(JEE Main 2022)]
(a) 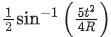
(b) 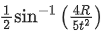
(c) 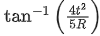
(d) 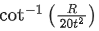
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: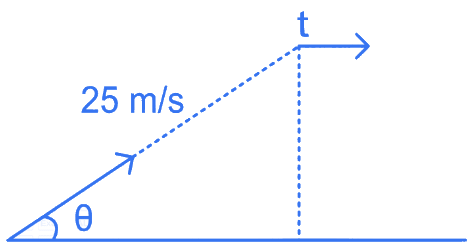
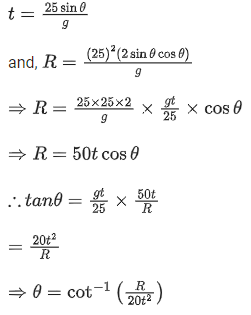
Q.14. Two buses P and Q start from a point at the same time and move in a straight line and their positions are represented by XP(t) = αt + βt2 and XQ(t) = ft − t2. At what time, both the buses have same velocity? [(JEE Main 2022)]
(a) 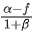
(b) 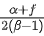
(c) 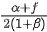
(d) 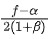
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: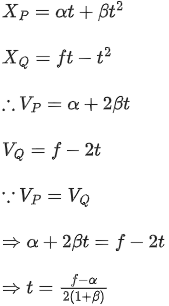
Q.15. Given below are two statements. One is labelled as Assertion A and the other is labelled as Reason R. [(JEE Main 2022)]
Assertion A : Two identical balls A and B thrown with same velocity 'u' at two different angles with horizontal attained the same range R. IF A and B reached the maximum height h1 and h2 respectively, then 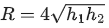
Reason R : Product of said heights.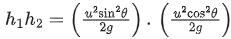
Choose the correct answer :
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is NOT the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: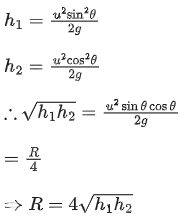
Q.16. A girl standing on road holds her umbrella at 45∘ with the vertical to keep the rain away. If she starts running without umbrella with a speed of 152 kmh−1, the rain drops hit her head vertically. The speed of rain drops with respect to the moving girl is : [(JEE Main 2022)]
(a) 30 kmh−1
(b) 25√2 kmh−1
(c) 30√2 kmh−1
(d) 25 kmh−1
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: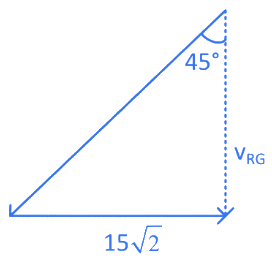
From graph,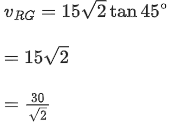
Q.17. A projectile is launched at an angle 'α' with the horizontal with a velocity 20 ms−1. After 10 s, its inclination with horizontal is 'β'. The value of tanβ will be : (g = 10 ms−2). [(JEE Main 2022)]
(a) tanα + 5secα
(b) tanα − 5secα
(c) 2tanα − 5secα
(d) 2tanα + 5secα
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: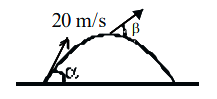 vy = 20×sinα − 10 × 10
vy = 20×sinα − 10 × 10
vx = 20cosα
∴ tanβ = vy / vx = 20sinα−100 / 20cosα
= tanα − 5secα
Q.18. Velocity (v) and acceleration (a) in two systems of units 1 and 2 are related as 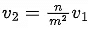 and a2 = a1 / mn respectively. Here m and n are constants. The relations for distance and time in two systems respectively are : [(JEE Main 2022)]
and a2 = a1 / mn respectively. Here m and n are constants. The relations for distance and time in two systems respectively are : [(JEE Main 2022)]
(a) 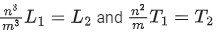
(b) 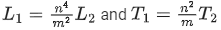
(c) 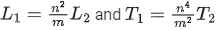
(d) 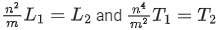
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
Similarly,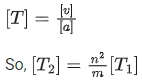
Q.19. A person can throw a ball upto a maximum range of 100 m. How high above the ground he can throw the same ball? [(JEE Main 2022)]
(a) 25 m
(b) 50 m
(c) 100 m
(d) 200 m
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: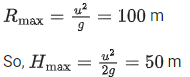
Q.20. A small toy starts moving from the position of rest under a constant acceleration. If it travels a distance of 10m in t s, the distance travelled by the toy in the next t s will be : [(JEE Main 2022)]
(a) 10 m
(b) 20 m
(c) 30 m
(d) 40 m
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: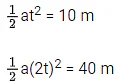
⇒ Distance travelled in next t s
= 40 − 10 = 30 m
Q.21. Two balls A and B are placed at the top of 180 m tall tower. Ball A is released from the top at t = 0 s. Ball B is thrown vertically down with an initial velocity 'u' at t = 2 s. After a certain time, both balls meet 100 m above the ground. Find the value of 'u' in ms−1. [use g = 10 ms−2] : [(JEE Main 2022)]
(a) 10
(b) 15
(c) 20
(d) 30
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
Let us assume that they meet at t = t0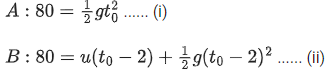
From (i), t0=4
⇒ 80 = 2u + 5(2)2
⇒ u = 30 m/s
Q.22. A projectile is fired from horizontal ground with speed v and projection angle θ. When the acceleration due to gravity is g, the range of the projectile is d. If at the highest point in its trajectory, the projectile enters a different region where the effective acceleration due to gravity is g′ = g / 0.81, then the new range is d′ = nd. The value of n is ___________ . [(JEE Advance 2022)]
 View Answer
View Answer 
Solution: (0.93and 0.97)
So, after entering in the new region, time taken by projectile to reach ground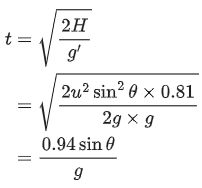
So, horizontal displacement done by the projectile in new region is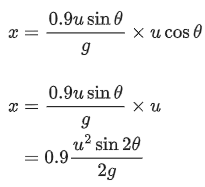
So, d′ = d / 2 + x
= 0.95d
So, n = 0.95d
Q.23. The ranges and heights for two projectiles projected with the same initial velocity at angles 42∘ and 48∘ with the horizontal are R1, R2 and H1, H2 respectively. Choose the correct option : [(JEE Main 2021)]
(a) R1 > R2 and H1 = H2
(b) R1 = R2 and H1 < H2
(c) R1 < R2 and H1 < H2
(d) R1 = R2 and H1 = H2
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Here, two projectiles are projected at angles 42∘ and 48∘ with same initial velocity.
As we know the expression of range of projectile,
Range = u2sin2θ / g
AT θ1 = 42∘,
Range, 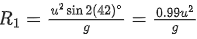
At θ2 = 48∘
Range, 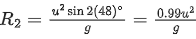
The range of the projectile is same for the two projectiles.
Therefore, R1 = R2
Now, as we know the expression of height of the projectile,
Higher the value of θ higher the value of maximum height. Therefore, H1 < H2.
Q.24. A helicopter is flying horizontally with a speed 'v' at an altitude 'h' has to drop a food packet for a man on the ground. What is the distance of helicopter from the man when the food packet is dropped? [(JEE Main 2021)]
(a) 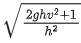
(b) 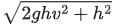
(c) 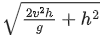
(d) 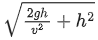
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: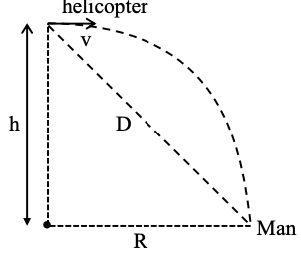
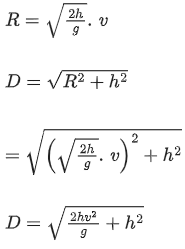
Option (c) is correct.
Q.25. A player kicks a football with an initial speed of 25 ms−1 at an angle of 45∘ from the ground. What are the maximum height and the time taken by the football to reach at the highest point during motion ? (Take g = 10 ms−2) [(JEE Main 2021)]
(a) hmax = 10 m
T = 2.5 s
(b) hmax = 15.625 m
T = 3.54 s
(c) hmax = 15.625 m
T = 1.77 s
(d) hmax = 3.54 m
T = 0.125 s
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: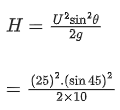
= 15.625 m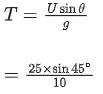
= 2.5 × 0.7
= 1.77 s
Q.26. Water drops are falling from a nozzle of a shower onto the floor, from a height of 9.8 m. The drops fall at a regular interval of time. When the first drop strikes the floor, at that instant, the third drop begins to fall. Locate the position of second drop from the floor when the first drop strikes the floor. [(JEE Main 2021)]
(a) 4.18 m
(b) 2.94 m
(c) 2.45 m
(d) 7.35 m
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: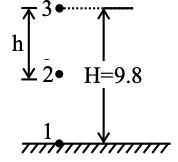
H = 1/2gt2
9.8 x 2 / 9.8 = t2
t = √2 sec
Δt : time interval between drops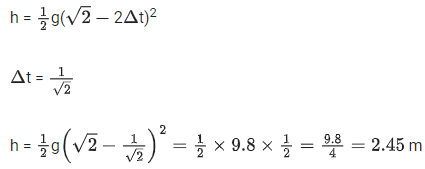
H − h = 9.8 − 2.45
= 7.35 m
Q.27. A bomb is dropped by fighter plane flying horizontally. To an observer sitting in the plane, the trajectory of the bomb is a : [(JEE Main 2021)]
(a) hyperbola
(b) parabola in the direction of motion of plane
(c) straight line vertically down the plane
(d) parabola in a direction opposite to the motion of plane
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Relative velocity of bomb w.r.t. observer in plane = 0.
Bomb will fall down vertically. So, it will move in straight line w.r.t. observer.
Q.28. A ball is thrown up with a certain velocity so that it reaches a height 'h'. Find the ratio of the two different times of the ball reaching h / 3 in both the directions. [(JEE Main 2021)]
(a) 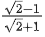
(b) 1/3
(c) 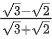
(d) 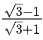
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: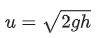
Now,
S = h / 3
a = −g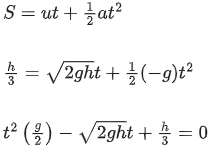
From quadratic equation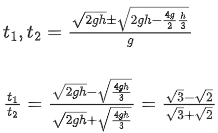
Q.29. The instantaneous velocity of a particle moving in a straight line is given as V = αt + βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is : [(JEE Main 2021)]
(a) 3α + 7β
(b) 3 / 2α + 7 / 3β
(c) α / 2 + β / 3
(d) 3 / 2α + 7 / 2β
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: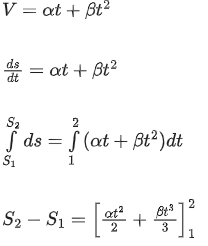
As particle is not changing direction
So distance = displacement
Distance = 
= 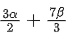
Q.30. A balloon was moving upwards with a uniform velocity of 10 m/s. An object of finite mass is dropped from the balloon when it was at a height of 75 m from the ground level. The height of the balloon from the ground when object strikes the ground was around :
(takes the value of g as 10 m/s2) [(JEE Main 2021)]
(a) 300 m
(b) 200 m
(c) 125 m
(d) 250 m
 View Answer
View Answer 
Correct Answer is Option (c)
Solution
- Object is projected as shown so as per motion under gravity
- Object takes t = 5 s to fall on ground
- Height of balloon from ground H = 75 + ut
- = 75 + 10 × 5 = 125 m
Q.31. The relation between time t and distance x for a moving body is given as t = mx2 + nx, where m and n are constants. The retardation of the motion is : (When v stands for velocity) [(JEE Main 2021)]
(a) 2 mv3
(b) 2 mnv3
(c) 2nv3
(d) 2n2v3
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: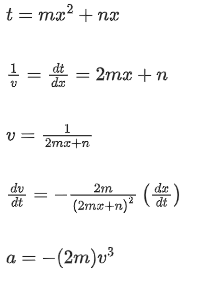
Q.32. Water droplets are coming from an open tap at a particular rate. The spacing between a droplet observed at 4th second after its fall to the next droplet is 34.3 m. At what rate the droplets are coming from the tap ? (Take g = 9.8 m/s2) [(JEE Main 2021)]
(a) 3 drops / 2 sconds
(b) 2 drops / second
(c) 1 drop / second
(d) 1 drop / 7 seconds
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
In 4 sec. 1st drop will travel
⇒1 / 2 × (9.8) × (4)2 = 78.4 m
∴ 2nd drop would have travelled
⇒ 78.4 − 34.3 = 44.1 m.
Time for 2nd drop
⇒ 1/2(9.8)t2 = 44.1
t = 3 sec
∴ each drop have time gap of 1 sec
∴ 1 drop per sec
Q.33. A boy reaches the airport and finds that the escalator is not working. He walks up the stationary escalator in time t1. If he remains stationary on a moving escalator then the escalator takes him up in time t2. The time taken by him to walk up on the moving escalator will be : [(JEE Main 2021)]
(a) 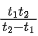
(b) 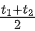
(c) 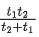
(d) t2 - t1
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
L = Length of escalator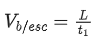
When only escalator is moving.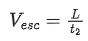
when both are moving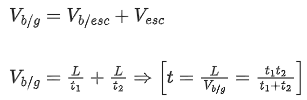
Q.34. A butterfly is flying with a velocity 4√2 m/s in North-East direction. Wind is slowly blowing at 1 m/s from North to South. The resultant displacement of the butterfly in 3 seconds is : [(JEE Main 2021)]
(a) 12√2 m
(b) 20 m
(c) 3 m
(d) 15 m
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: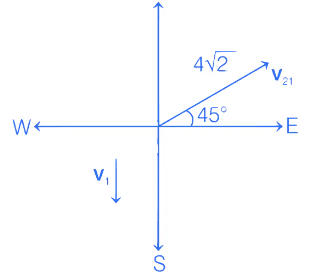
In the above figure, v1 is the speed of wind and v21 is the speed of butterfly with respect to wind.
So, v21 can be given as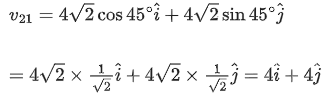
and v1 can be given as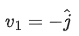
∴ Velocity of butterfly can be given as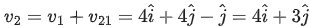
Displacement of butterfly, D = v2 × t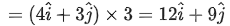
∴ Magnitude of displacement, 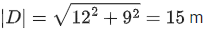
Q.35. The velocity − displacement graph of a particle is shown in the figure. [(JEE Main 2021)] The acceleration − displacement graph of the same particle is represented by :
The acceleration − displacement graph of the same particle is represented by :
(a)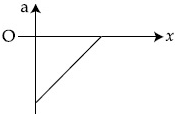
(b)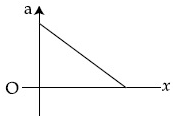
(c)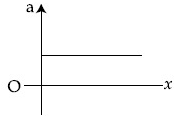
(d)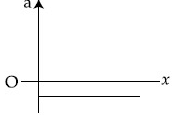
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
The slope of the given v versus x graph is m= −v0 / x0 and intercept is c = + v0. Hence, v varies with x as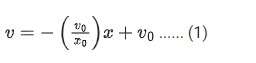
where v0 and x0 are constants of motion. Differentiating with respect to time t, we have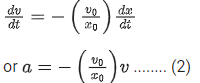
Using Eq. (1) in Eq. (2), we get
Thus the graph of a versus x is a straight line having a positive slope = 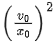 and negative intercept =
and negative intercept = 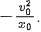 Hence the correct choice is (a).
Hence the correct choice is (a).
Q.36. The position, velocity and acceleration of a particle moving with a constant acceleration can be represented by : [(JEE Main 2021)]
(a)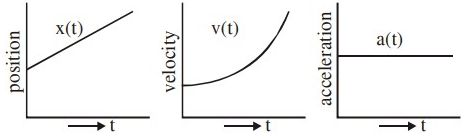
(b)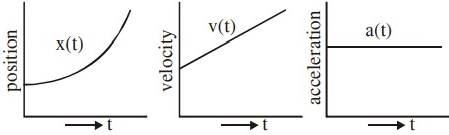
(c)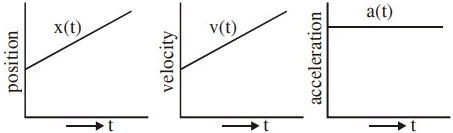
(d)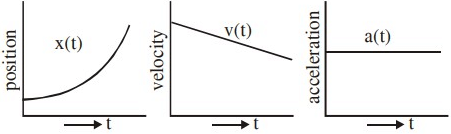
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Acceleration(a) is constant
∴ v ∝ t (straight line graph)
and x ∝ t2 (parabolic graph)
Q.37. A rubber ball is released from a height of 5 m above the floor. It bounces back repeatedly, always rising to 81 / 100 of the height through which it falls. Find the average speed of the ball. (Take g = 10 ms−2) [(JEE Main 2021)]
(a) 2.50 ms−1
(b) 3.0 ms−1
(c) 2.0 ms−1
(d) 3.50 ms−1
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 
Total distance d = h + 2e2h + 2e4h + 2e6h + 2e8h + ......
d = h + 2e2h (1 + e2 + e4 + e6 + .......)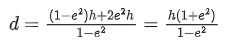
Total time = T + 2eT + 2e2T + 2e3T + .......
Total time = T + 2eT (1 + e + e2 + e3 + .......)
Average speed of the ball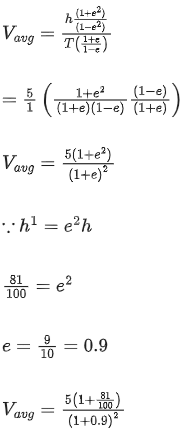
= 2.50 m/sec.
Q.38. A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate to come to rest. If the total time elapsed is t seconds, the total distance travelled is: [(JEE Main 2021)]
(a) 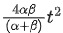
(b) 
(c) 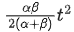
(d) 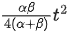
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 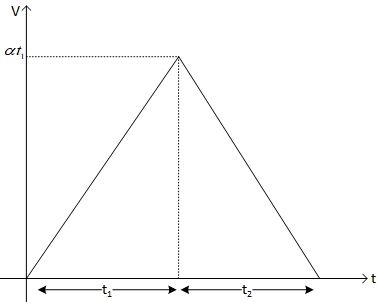
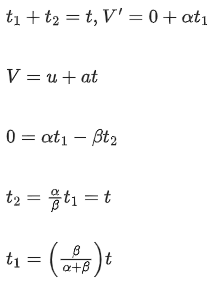
Distance = 1/2 (t1 + t2) x αt1 (area of triangle)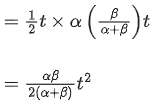
Q.39. A mosquito is moving with a velocity 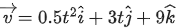 m/s and accelerating in uniform conditions. What will be the direction of mosquito after 2 s? [(JEE Main 2021)]
m/s and accelerating in uniform conditions. What will be the direction of mosquito after 2 s? [(JEE Main 2021)]
(a) 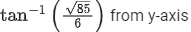
(b) 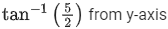
(c) 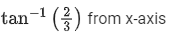
(d) 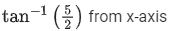
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 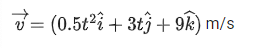
At t = 2 s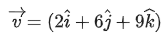
Direction cosine along y-axis,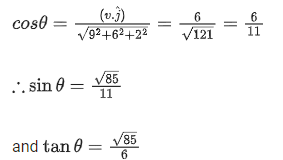
Mosquito make angle 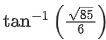 from y-axis.
from y-axis.
Q.40. The velocity-displacement graph describing the motion of bicycle is shown in the figure. [(JEE Main 2021)]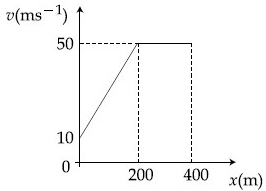 The acceleration-displacement graph of the bicycle's motion is best described by :
The acceleration-displacement graph of the bicycle's motion is best described by :
(a)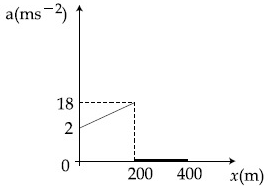
(b)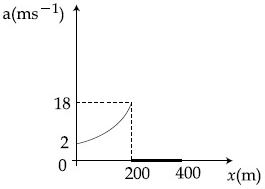
(c)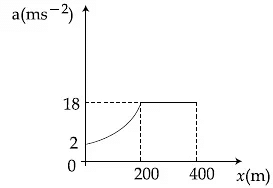
(d)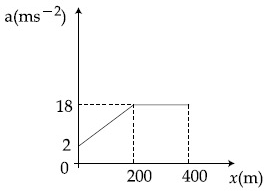
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
We know that, 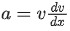
as slope is constant, so a v (from x = 0 to 200 m)
& slope = 0 so a = 0 (from x = 200 to 400 m)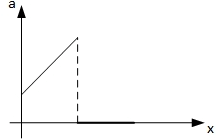
Q.41. The trajectory of a projectile in a vertical plane is y = αx βx2, where and are constants and x & y are respectively the horizontal and vertical distances of the projectile from the point of projection. The angle of projection and the maximum height attained H are respectively given by: [(JEE Main 2021)]
(a) 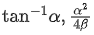
(b) 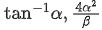
(c) 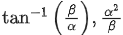
(d) 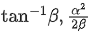
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
y = αx βx2,
comparing with trajectory equation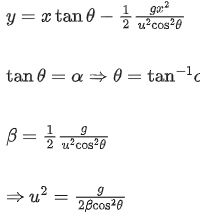
Maximum height H :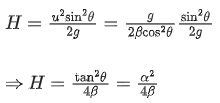
Q.42. A scooter accelerates from rest for time t1 at constant rate a1 and then retards at constant rate a2 for time t2 and comes to rest. The correct value of wil be : [(JEE Main 2021)]
(a) 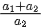
(b) 
(c) a2 / a1
(d) a1 / a2
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 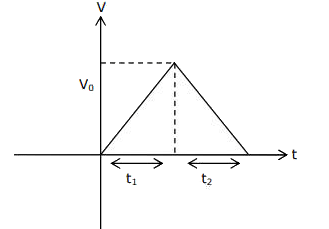
From given information :
For 1st interval
v0 = a1 t1 ....... (1)
For 2nd interval
v0 = a2 t2 ..... (2)
from (1) & (2)
a1 t1 = a2 t2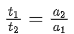
Q.43. A stone is dropped from the top of a building. When it crosses a point 5 m below the top, another stone starts to fall from a point 25 m below the top. Both stones reach the bottom of building simultaneously. The height of the building is : [(JEE Main 2021)]
(a) 50 m
(b) 25 m
(c) 45 m
(d) 35 m
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 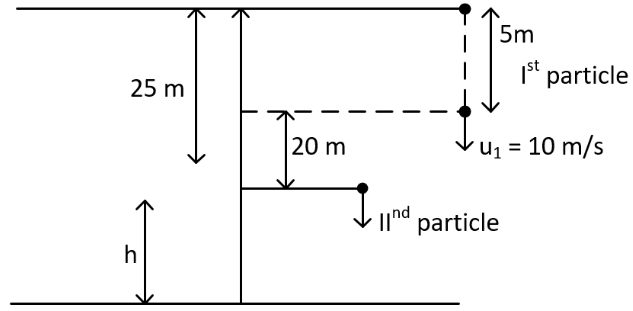
For particle (1)
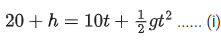
For particle (2)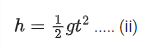
put equation (ii) in equation (i)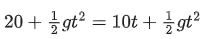
t = 2 sec.
Put in equation (ii)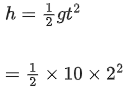
h = 20 m
The height of the building =25+20 = 45 m
Q.44. In an octagon ABCDEFGH of equal side, what is the sum of [(JEE Main 2021)]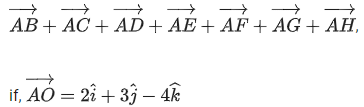
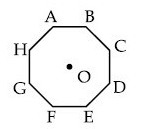 (a)
(a) 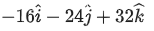
(b) 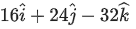
(c) 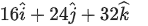
(d) 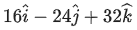
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 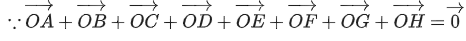
By triangle law of vector addition, we can write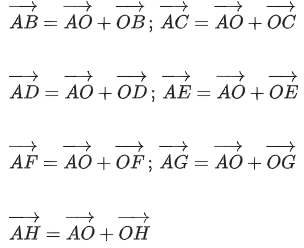
Now
Q.45. An engine of a train, moving with uniform acceleration, passes the signal-post with velocity u and the last compartment with velocity v. The velocity with which middle point of the train passes the signal post is : [(JEE Main 2021)]
(a) 
(b) 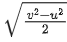
(c) 
(d) 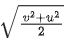
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 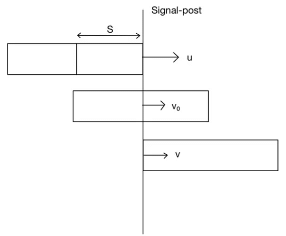
Let initial speed of train u. When midpoint of the train reach the signal post it's velocity becomes v0.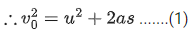
When train passes the signal post completely it's velocity becomes v.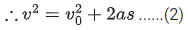
Subtracting (2) from (1) we get,
Q.46. If the velocity-time graph has the shape AMB, what would be the shape of the corresponding acceleration-time graph? [(JEE Main 2021)]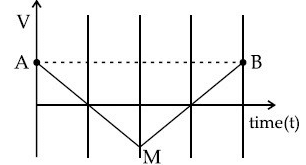
(a)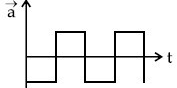
(b)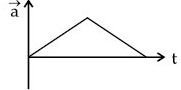
(c)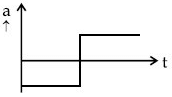
(d)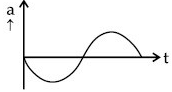
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 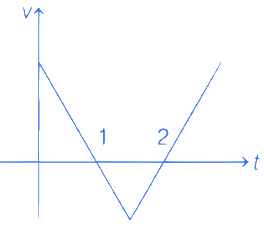
From the graph for first line, the slope is negative and intercept is positive.
So, equation of line is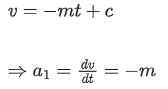
Similarly, for second line, the slope is positive and intercept is negative, so equation of line is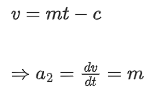
∴ The corresponding acceleration-time graph as shown below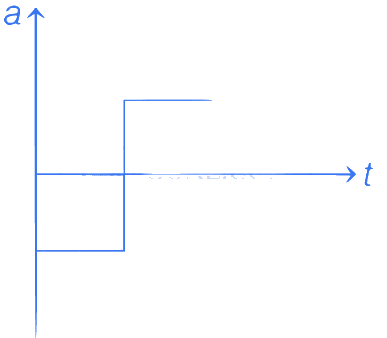
Hence, option (a) is correct.
Q.47. A particle is moving along the x-axis, with its coordinate as a function of time given by x(t) =10+ 8t - 3t2. Another particle is moving along the y-axis with its coordinate as a function of time given by y(t) = 5 - 8t3. At t = 1s, the speed of the second particle as measured in the frame of the first particle is given as √v. Then v (in m/s) is ______. [2020]
 View Answer
View Answer 
Solution: 580
Given that
x(t) =10+ 8t - 3t2, y(t) = 5 - 8t3
So,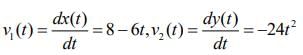
At t = 1 s, we have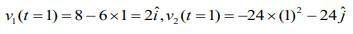
Relative velocity of second particle with respect to first particle is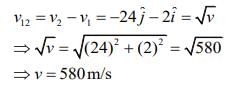
Q.48. A particle moves such that it's position vector is 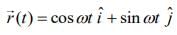 where ω is a constant and t is time. Then which of the following statements is true for the velocity
where ω is a constant and t is time. Then which of the following statements is true for the velocity 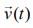 and acceleration
and acceleration  of the particle.
of the particle.
(a) 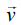 is perpendicular to
is perpendicular to 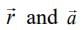 is directed away from the origin.
is directed away from the origin.
(b) 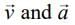 both are perpendicular to
both are perpendicular to 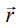
(c) 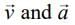 both are parallel to
both are parallel to 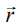
(d)  is perpendicular to
is perpendicular to 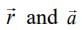 is directed towards the origin.
is directed towards the origin.
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
Given that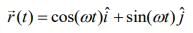
So,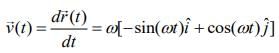
and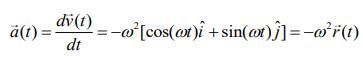
Since, 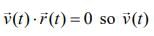 is perpendicular to
is perpendicular to 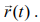
And 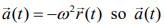 had opposite direction to
had opposite direction to 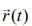 or antiparallel to
or antiparallel to 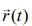 that is, directed towards the origin.
that is, directed towards the origin.
Q.49. A ball is dropped from the top of a 100 m high tower on a planet. In the last (1/2)s before hitting the ground, it covers a distance of 19 m. Acceleration due to gravity (in m/s2) near the surface on that planet is _______.
 View Answer
View Answer 
Solution: 8
Given that
u = 0 m/s, H = 100 m, d = 19 m, t = 1/2 s
Let time taken to tavel (H – h) distance be t.
So,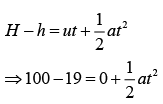
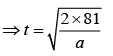 ..(1)
..(1)
Now, time taken to hit the ground is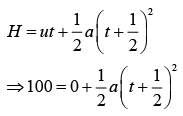
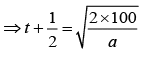 ..(2)
..(2)
From Eqs. (1) and (2), we get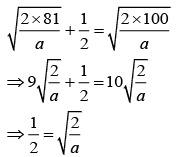
⇒ a = 8 m/s2
Q.50. A particle starts from the origin at t = 0 with an initial velocity of 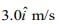 and moves in the x-y plane with a constant acceleration
and moves in the x-y plane with a constant acceleration 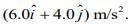 The x-coordinate of the particle at the instant when its y-coordinate is 32 m is D m. The value of D is
The x-coordinate of the particle at the instant when its y-coordinate is 32 m is D m. The value of D is
(a) 32
(b) 50
(c) 60
(d) 40
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Given that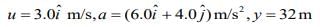
From the equation of motion in two dimensions, we have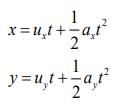
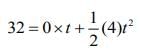
⇒ t2 = 16
⇒ t = 4 s
So,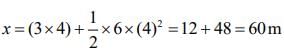
Q.51. The distance x covered by a particle in one dimensional motion varies with time t as x2 = at2 + 2bt + c. If the acceleration of the particle depends on x as x−n, where n is an integer, the value of n is ______.
 View Answer
View Answer 
Solution: 3
x2 = at2 + 2bt + c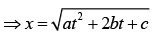 .. (1)
.. (1)
Velocity is given by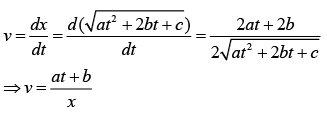
⇒ vx = at + b ..(2)
Acceleration is given by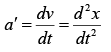
Differentiate Eq. (2) with respect to t, we get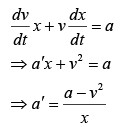
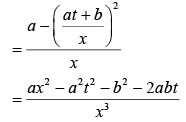
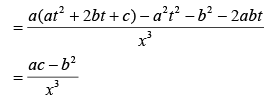
So,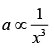
Therefore, n = 3
Q.52. In a car race on straight road, car A takes a time t less than car B at the finish and passes finishing point with a speed v more than that of car B. Both the cars start from rest and travel with constant acceleration a1 and a2, respectively. Then v is equal to [JEE Main 2019]
(a) 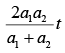
(b) 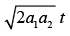
(c) 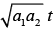
(d) 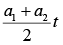
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Let time taken by car A is t'
vB = a2(t' +t)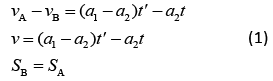
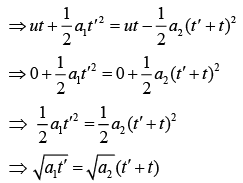
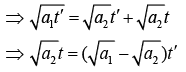
Put this value in Eq. (1), we get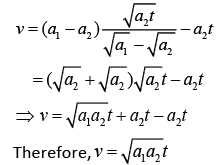
Q.53. A passenger train of length 60 m travels at a speed of 80 km/hr. Another freight train of length 120 m travels at a speed of the. The ratio of times taken by the passenger train to completely cross the freight train when (i) they are moving in same direction and (ii) in the opposite directions is [JEE Main 2019]
(a) 11/5
(b) 5/2
(c) 3/2
(d) 25/11
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
Let passenger train and freight train be A and B and vA is the velocity of passenger train and vB is the velocity of freight train B.
Relative velocity of A with respect to B is (same direction)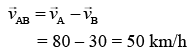
Time taken by the train A to cross the train B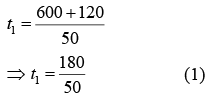
Train moving in opposite direction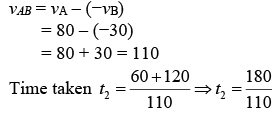
Therefore, required ratio is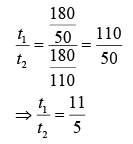
Q.54. A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5 s? (JEE Main 2019)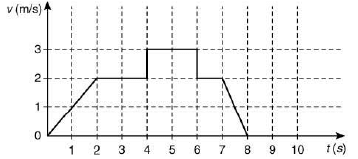
(a) 10 m
(b) 6 m
(c) 3 m
(d) 9 m
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
As we know that, area under v-t curve gives displacement.
therefore,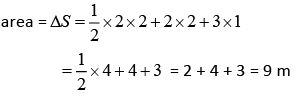
Q.55. A particle is moving with a velocity 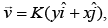 where K is a constant. The general equation for its path is (JEE Main 2019)
where K is a constant. The general equation for its path is (JEE Main 2019)
(a) y = x2 + constant
(b) y2 = x + constant
(c) y2 = x2 + constant
(d) xy = constant
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Equation for velocity of the particle is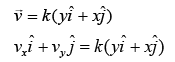
Thus,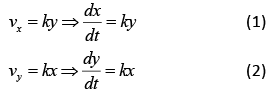
Now,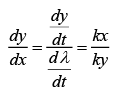
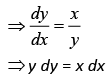
Integrating both the sides, we get
y2 = x2 + constant
Q.56. The position coordinates of a particle moving in a 3D coordinate system is given by
x = a cos ωt
y = a sin ωt
and
z = aωt
The speed of the particle is (JEE Main 2019)
(a) 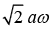
(b) aω
(c) 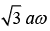
(d) 2aω
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
Velocity coordinates of particle is obtained by differentiating the position coordinate with respect to time, Thus: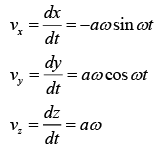
Hence, velocity of particle is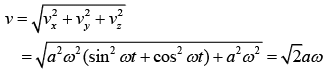
Q.57. In the cube of side a, as shown in the figure, the vector from the central point of the face ABOD to the central point of the face BEFO will be (JEE Main 2019)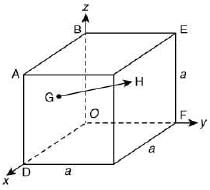
(a) 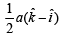
(b) 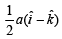
(c) 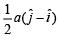
(d) 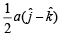
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Side of a cube is a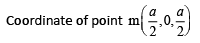
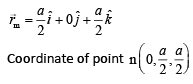
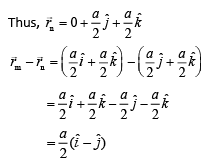
Q.58. Two guns A and B can fire bullets at speeds 1 km/s and 2 km/s respectively. From a point on a horizontal ground, they are fired in all possible directions. The ratio of maximum areas covered by the bullets fired by the two guns, on the ground is (JEE Main 2019)
(a) 1 : 16
(b) 1 : 2
(c) 1 : 4
(d) 1 : 8
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
Area covered = πR2
A ∝ R
Thus, range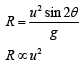

Therefore, required ratio is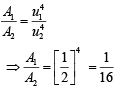
Q.59. Two vectors 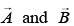 have equal magnitudes. The magnitude of
have equal magnitudes. The magnitude of
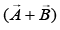 is n times the magnitude of
is n times the magnitude of 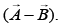 The angle between
The angle between 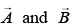 is (JEE Main 2019)
is (JEE Main 2019)
(a) 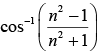
(b) 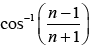
(c) 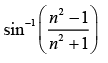
(d) 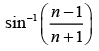
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
We know that
According to the question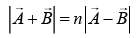
Squaring both the sides, we get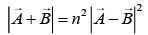
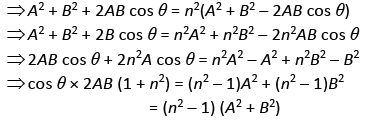
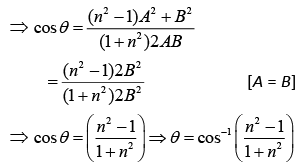
Q.60. A body is projected at t = 0 with a velocity 10 m/s at an angle of 60° with the horizontal. The radius of curvature of its trajectory at t = 1 s is R. Neglecting air resistance and taking acceleration due to gravity g = 10 m/s2, the value of R is (JEE Main 2019)
(a) 2.5 m
(b) 2.8 m
(c) 10.3 m
(d) 5.1 m
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
At t = 1: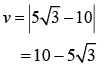
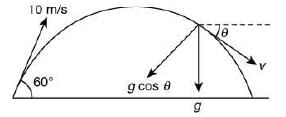
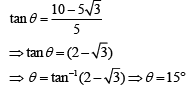
The radius of curvature of the trajectory is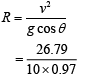
= 2.77 m = 2.8 m
Q.61. A particle moves from the point 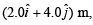 at t = 0 with an initial velocity
at t = 0 with an initial velocity 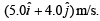 It is acted upon by a constant force which produces a consult acceleration
It is acted upon by a constant force which produces a consult acceleration 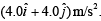 What is the distance of the particle from the origin at time 2s? (JEE Main 2019)
What is the distance of the particle from the origin at time 2s? (JEE Main 2019)
(a) 15m
(b) 20√2m
(c) 5m
(d) 10√2m
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 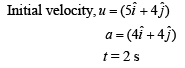
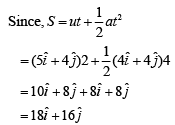
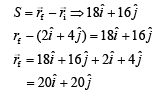
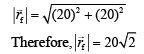
Q.62. All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up. (JEE Main 2018)
(1)
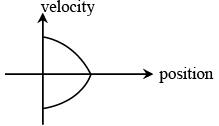
(2)
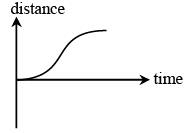
(3)
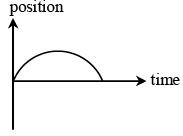
(4)
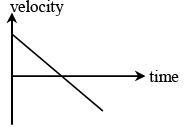
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
n graph ‘2’ initial slope is zero which is not possible, since initial velocity is non-zero in all other three graphs.
Q.63. An automobile, travelling at 40 km/h, can be stopped at a distance of 40m by applying brakes. If the same automobile is travelling at 80 km/h, the minimum stopping distance, in metres, is (assume no skidding): (JEE Main 2018)
(a) 75 m
(b) 160 m
(c) 150 m
(d) 100 m
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 
Q.64. The velocity-time graphs of a car and a scooter are shown in the figure. (i) The difference between the distance travelled by the car and the scooter in 15 s and (ii) the time at which the car will catch up with the scooter are, respectively. (JEE Main 2018)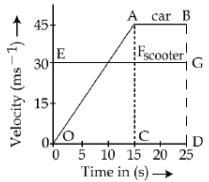
(a) 337.5 m and 25 s
(b) 225.5 m and 10 s
(c) 112.5 m and 15 s
(d) 112.5 m and 22.5 s
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
The distance traveled in 15 seconds by both will be given by area under curve.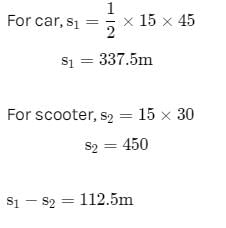
Suppose after time t, they will meet, then distance traveled by both of them will be equal.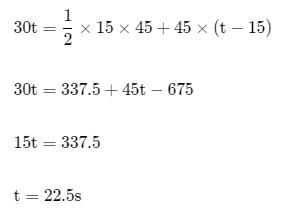
Q.65. Let 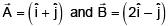 The magnitude of a coplanar vector
The magnitude of a coplanar vector 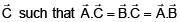 is given by: (JEE Main 2018)
is given by: (JEE Main 2018)
(a) 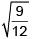
(b) 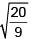
(c) 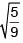
(d)
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 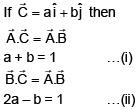
Solving equation (i) and (ii) we get
Q.66. Which graph corresponds to an object moving with a constant negative acceleration and a positive velocity? (JEE Main 2017)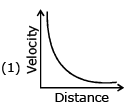

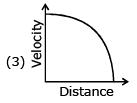
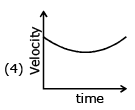
 View Answer
View Answer 
Correct Answer is Option (3)
Solution: 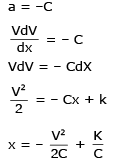
Q.67. A car is standing 200 m behind a bus, which is also at rest. The two start moving at the same instant but with different forward accelerations. The bus has acceleration 2 m/s2 and the car has acceleration 4 m/s2. The car will catch up with the bus after a time of (JEE Main 2017)
(a) 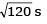
(b) 15 s
(c) 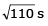
(d) 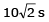
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 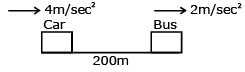
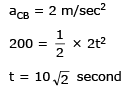
FAQs on JEE Main Previous Year Questions (2016- 2025): Motion
| 1. What are the important topics in motion for JEE Main preparation? |  |
| 2. How can I improve my problem-solving skills in motion-related questions for JEE Main? |  |
| 3. Are there any specific formulas I should memorize for motion in JEE Main? |  |
| 4. How can I relate JEE Main motion questions to real-life scenarios? |  |
| 5. What strategies can I use to tackle difficult motion problems in JEE Main? |  |















