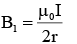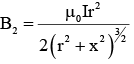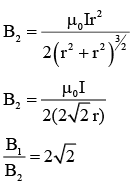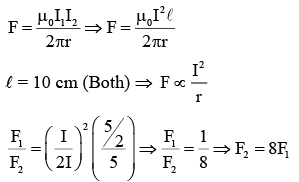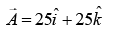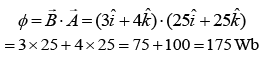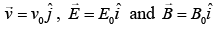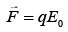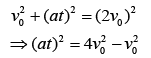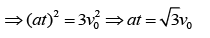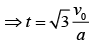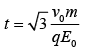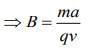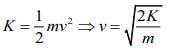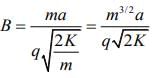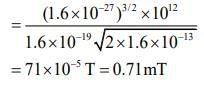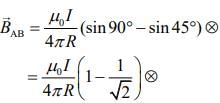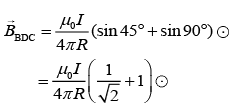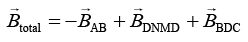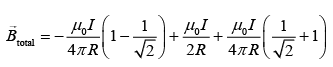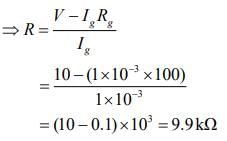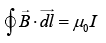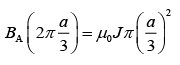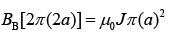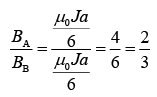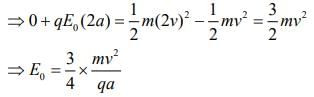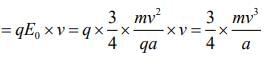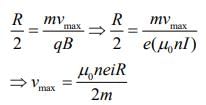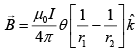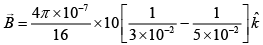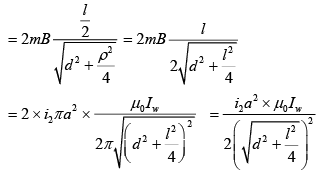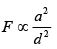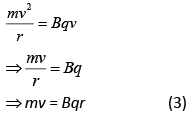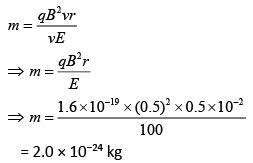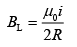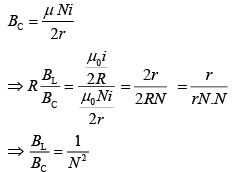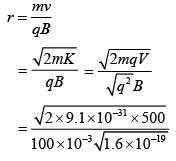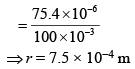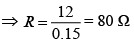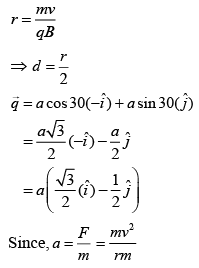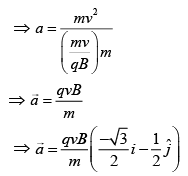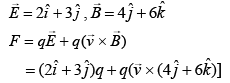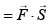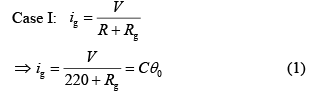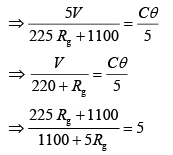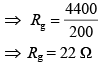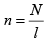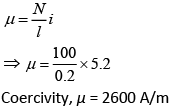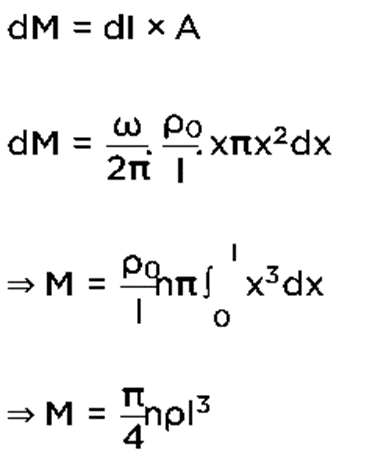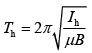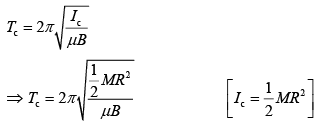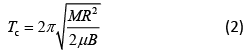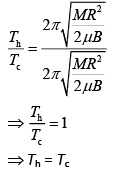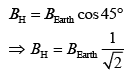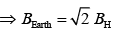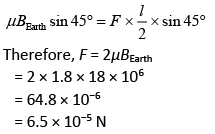Q.1. A circular loop of radius 𝑟 is carrying current I A. The ratio of magnetic field at the center of circular loop and at a distance 𝑟 from the center of the loop on its axis is: [JEE Main 2023]
(1) 2√2: 1
(2) 1: 3√2
(3) 1: √2
(4) 3√2: 2
Ans. (1)
Magnetic field at centre of coil
on the axis at x = r ⇒
Q.2. Two long straight wires P and Q carrying equal current 10 A each were kept parallel to each other at 5 cm distance. Magnitude of magnetic force experienced by 10 cm length of wire P is F1 - If distance between wires is halved and currents on them are doubled, force F2 on 10 cm length of wire P will be: [JEE Main 2023]
(1) F1/8
(2) 8F1
3) 10 F1
(4) F1/10
Ans. (2)
Q.3. The figure gives experimentally measured B vs H variation in a ferromagnetic material. The retentivity, co - ercivity and saturation, respectively, of the material are [2020]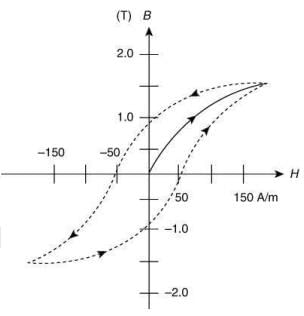 (1) 1.5 T, 50 A/m and 2.0 T
(1) 1.5 T, 50 A/m and 2.0 T
(2) 1.5 T, 50 A/m and 1.0 T
(3) 150 A/m, 1.0 T and 1.0 T
(4) 1.0 T, 50 A/m and 1.5 T
Ans: (4)
From the given graph, we have
Retentivity = 1.0 T
It is the ability of a substance to retain or resist magnetization.
Coercivity = 50 A/m
It is the resistance of a magnetic material to changes in magnetization.
And Saturation = 1.5 T
Q.4. Consider a circular coil of wire carrying constant current I, forming a magnetic dipole. The magnetic flux through an infinite plane that contains the circular coil and excluding the circular coil area is given by ϕi. The magnetic flux through the area of the circular coil area is given by ϕ0. Which of the following option is correct? [2020]
(1) ϕi = ϕ0
(2) ϕi > ϕ0
(3) ϕi < ϕ0
(4) ϕi =−ϕ0
Ans: (4)
Given, circular coil curving current and forming magnetic dipole.
ϕi is magnetic flux through an infinite plane containing circular coil and excluding circular coil area.
ϕ0 is magnetic flux through the area of circular coil.
Since, magnetic field forms closed loop so magnetic flux passing through area of circular coil and outside must be equal but opposite in direction
Therefore,
ϕi = -ϕ0
Q.5. A loop ABCDEFA of straight edges has six corner points A(0, 0, 0), B(5, 0, 0), C(5, 5, 0), D(0, 5, 0), E(0,5, 5) and F(0, 0, 5). The magnetic field in this region is 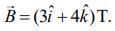 The quantity of flux through the loop ABCDEFA (in Wb) is ______. [2020]
The quantity of flux through the loop ABCDEFA (in Wb) is ______. [2020]
Ans: 175 Wb
Given that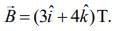
Corner points of loop ABCDEFA are A(0, 0, 0), B(5, 0, 0), C(5, 5, 0), D(0, 5, 0), E(0, 5, 5) and F(0, 0, 5).
Area vector of loop is
Magnetic flux is given by
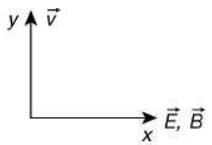
Q.6. A particle of mass m and charge q has an initial velocity 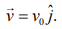 If an electric field
If an electric field 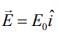 and magnetic field
and magnetic field 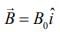 act on the particle, its speed will double after a time [2020]
act on the particle, its speed will double after a time [2020]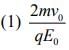
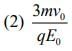
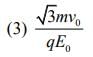
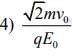
Ans: (3)
Given that
Force acting on charge along x-axis is
So, acceleration is(1)
We need to find the time when speed will be double, that is,
From Eq. (1), we get
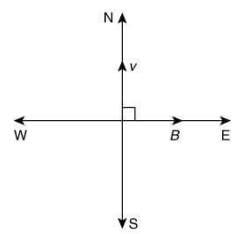
Q.7. Proton with kinetic energy of 1 MeV moves from south to north. It gets an acceleration of 1012 m/s2 by an applied magnetic field (west to east). The value of magnetic field (Rest mass of proton is 1.6 × 10−27 kg) [2020]
(1) 0.71 mT
(2) 7.1 mT
(3) 0.071 mT
(4) 71 mT 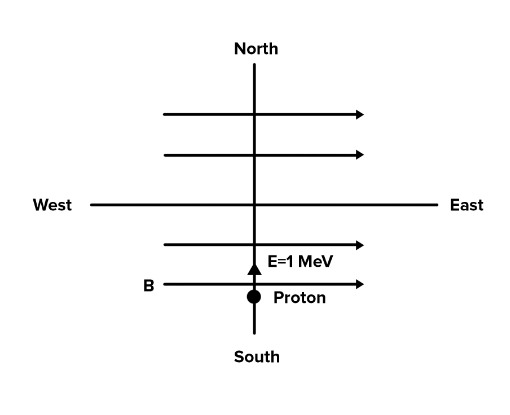
Ans: (1)
Given that
K = 1MeV = 1 x 106 x 1.6 x 10-19 J = 1.6 x 10-13 J
mp = 1.6 x 10-27 kg, q = 1.6 x 10-16 C
a = 1012 m/s2
Force on a moving charge particle in a magnetic field is given by
F qvB = sinθ
Here θ = 900
So,
F = qvB
and F = ma
So, ma = qvB
We know that
Then,
Q.8. A very long wire ABDMNDC is shown in figure carrying current I. AB and BC parts are straight, long and at a right angle. At D, wire forms a circular turn DMND of radius R. AB, BC parts are tangential to circular turn at N and D. Magnetic field at the centre of circle is [2020]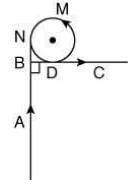
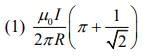
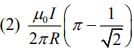
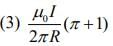

Ans: (1)
There are three magnetic fields act at the centre of the circle, that is
Magnetic field due to straight part of wire AB, that is,
Since, perpendicular distance between wire part AB and centre of circle is R. Direction of field of inside the paper.
Magnetic field due to circular part of wire DMND, that is,
Direction of field is outside the paper.
Magnetic field due to straight part of wire BDC, that is,
Since, perpendicular distance between wire part BDC and centre of circle is R. Direction of field is outside the paper.
Therefore, total magnetic field act at the centre of the circle DMND is given bySince, we are taking the direction outside the paper as reference so the inside magnetic field become negative.
So,
Q.9. A galvanometer having a coil resistance 100 Ω gives a full scale deflection when a current of 1 mA is sped through it. What is the value of the resistance which can convert this galvanometer into a voltmeter giving full scale deflection for a potential difference of 10 V? [2020]
(1) 10 kΩ
(2) 8.9 kΩ
(3) 7.9 kΩ
(4) 9.9 kΩ
Ans: (4)
Given that
Rg = 100Ω, Ig = 1mA = 1 x 10-3A, V = 10V
To make galvanometer to voltmeter, we add a resistance in series
So,
V = Ig(R + Rg)
Q.10. A long, straight wire of radius 'a' carries a current distributed uniformly over its cross-section. The ratio of the magnetic fields due to the wire at distance a/3 and 2a, respectively from the axis of the wire is [2020]
(1) 2/3
(2) 2
(3) 1/2
(4) 3/2
Ans: (1)
Given condition is shown in the following circuit figure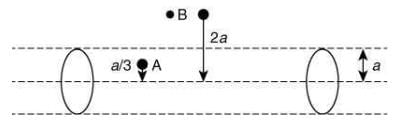
Let current density of the given wire b J
Applying Ampere's law, we haveAt point A distance a/3, we get
(1)
At point B distance 2a , we get(2)
From Eqs. (1) and (2), we get
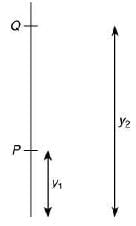
Q.11. A charged particle of mass m and charge q moving under the influence of uniform electric field 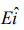 and a uniform magnetic field
and a uniform magnetic field 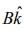 follows a trajectory from point P to Q as shown in figure. The velocities at P and Q are respectively,
follows a trajectory from point P to Q as shown in figure. The velocities at P and Q are respectively, 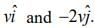 Then which of the following statements (A, B, C, D) are correct? (Trajectory shown is schematic and is not to scale) [2020]
Then which of the following statements (A, B, C, D) are correct? (Trajectory shown is schematic and is not to scale) [2020]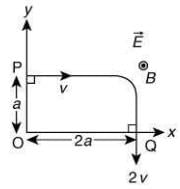
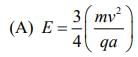
(B) Rate of work done by the electric field at P is 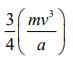
(C) Rate of work done by both the fields at Q is zero
(D) The difference between the magnitude of angular momentum of the particle at P and Q is 2 mav.
(1) (A), (C), (D)
(2) (B), (C), (D)
(3) (A), (B), (C)
(4) (A), (B), (C), (D)
Ans: (3)
Solving for point (A):
From work energy theorem, we have
WMF + WEF = ΔK
So, point (A) is true.
Solving for point (B):
Rate of work done by electric filed = Power of electric field
Power of electric filed = FEF x v
So, point (B) is true.
Solving for point (C):
At point Q,
Total rate of work done = Rate of work done by electric filed + Rate of work done by magnetic field
Rate of work done by magnetic field = 0 W (Since, force and displacement are perpendicular)
Rate of work done by electric field = 0 W (Since, force and displacement are perpendicular)
Therefore, total rate of work done at point Q by both fields = 0 W
So, point (C) is true
Solving for point (D):
Initial angular momentum is
Li = fmva
Final angular momentum is
Lf = m(2v)(2a) =4mva
Change in angular momentum is
ΔL = Lf - Li = 4mva - mva = 3mva
So, point (D) is not true.
Q.12. An electron gun is placed inside a long solenoid of radius R on its axis. The solenoid has n turns/length and carries a current I. The electron gun shoots an electron along the radius of the solenoid with speed v. If the electron does not hit the surface of the solenoid, maximum possible value of v is (all symbols have their standard meaning) [2020]
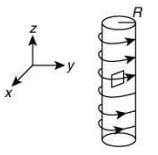
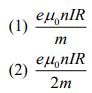
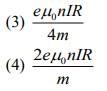
Ans: (2)
The maximum possible radius of electron for which it does not hit the surface is
r = R/2 .. (1)
Radius of circular motion of a charge particle in a magnetic field is given by
r = mv/qB .. (2)
From Eqs. (1) and (2), we get
Q.13. A current loop, having two circular arcs joined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to [2019]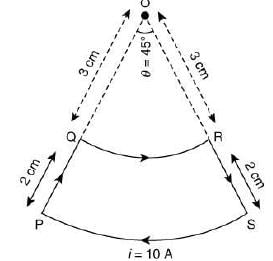
(1) 1.0 × 10−7 T
(2) 1.5 × 10−7 T
(3) 1.5 × 10−5 T
(4) 1.0 × 10−5 T
Ans: (4)
Let B be the magnetic field at point O due to are of radius r.
Given r1 = 3 cm = 3 × 10−2 m, r2 = 5 cm = 5 × 10−2 cm,
Therefore,
Since, both arcs have opposite direction of current
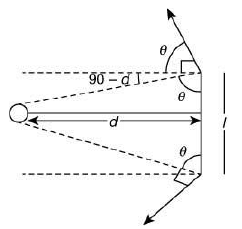
Q.14. An infinitely long current-carrying wire and a small current-carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its center from the wire is d (d ≫ a). If the loop applies a force F on the wire, then [2019]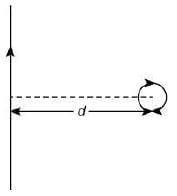

Ans: (4)
Let the effective length of magnet be l.
So, magnetic moment is
M = i2πa2 × n (number of turns, n = 1)
= i2πa2 = ml
Suppose iw is the current flowing through the wire. The force on north pole of magnet = mB and the force on south pole of magnet = mB. Then, resultant force is
F = 2mBcosθ
l << d, so l can be neglected.
Therefore,
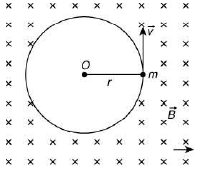
Q.15. A particle having the same charge as of electron moves in a circular path of radius 0.5 cm under the influence of a magnetic field of 0.5 T. If an electric field of 100 V/m makes it to move in a straight path, the mass of the particle is (Given charge of electron = 1.6 × 10−19 C) [2019]
(1) 9.1 × 10−31 kg
(2) 1.6 × 10−27 kg
(3) 1.6 × 10−19 kg
(4) 2.0 × 10−24 kg
Ans: (4)
Suppose a particle of mass m and charge q, entering a uniform magnetic field induction B at O with velocity V.
The force acting on the charge particle due to magnetic field is
The force F on the charged particle due to magnetic field provides the required centripetal force necessary for motion along the circular path of radius r
From Eq. (1) and Eq. (2), we get
Force due to electric field is
F = qE
Since, both are in straight line, then
qvB = qE
⇒ E = vB (4)
From Eq. (3) and Eq. (4), we have
Q.16. One of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current is passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the centre of the coil (BC), that is,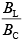 will be [2019]
will be [2019]
(1) N
(2) 1/N
(3) N2
(4) 1/N2
Ans: (4)
Let R be the radius of loop and r be the radius of circular coil of N turn.For Loop,
L = 2πR (1)
For coil,
L = N × 2πr (2)
Fron Eq.(1) and Eq. (2), we get
R = Nr
Magnetic field at the centre of loop is
Magnetic field at the centre of coil is
Q.17. In an experiment, electrons are accelerated, from rest, by applying a voltage of 500 V. Calculate the radius of the path if a magnetic field 100 mT is then applied. (Charge of the electron = 1.6 × 10−19 C Mass of the electron = 9.1 × 10−31 kg) [2019]
(1) 7.5 × 10−3 m
(2) 7.5 m
(3) 7.5 × 10−2 m
(4) 7.5 × 10−4 m
Ans: (4)
We know
Q.18. A galvanometer having a resistance of 20 Ω and 30 divisions on both sides has figure of merit 0.005 ampere/division. The resistance that should be connected in series such that it can be used as a voltmeter up to 15 V, is [2019]
(1) 100 Ω
(2) 120 Ω
(3) 80 Ω
(4) 125 Ω
Ans: (3)
Deflection current is
i0 = nk
= 30 × 0.005Thus, V = IR
⇒ 15 = (0.05 × 30 × 20) + (30 × 0.005 × R)⇒ 15 = 3 + 0.15R
Q.19. The region between y = 0 and y = d contains a magnetic field 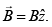 A particle of mass m and charge q enters the region with a velocity
A particle of mass m and charge q enters the region with a velocity 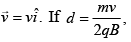 the acceleration of the charged particle at the point of its emergence at the other side is [2019]
the acceleration of the charged particle at the point of its emergence at the other side is [2019]
(1) 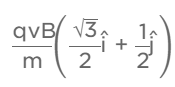
(2) 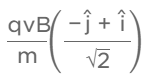
(3) 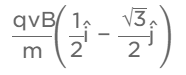
(4) 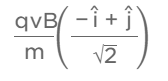
Ans: (3)
*Disputed question – None of the options is correct.
Let us suppose that particles enter from circular path with center (0, d).Radius of circular path is
Q.20. A particle of mass m and charge q is in an electric and magnetic field given by 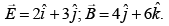 The charged particle is shifted from the origin to the point P (x = 1; y = 1) along a straight path. The magnitude of the total work done is [2019]
The charged particle is shifted from the origin to the point P (x = 1; y = 1) along a straight path. The magnitude of the total work done is [2019]
(1) (0.35)q
(2) (5)q
(3) (2.5)q
(4) (0.15)q
Ans: (2)
Electric and magnetic field is given by
Work done by magnetic force = 0
So,
Therefore, work done by electric field
Q.21. The galvanometer deflection, when key K1 is closed but K2 is open, equals θ0 (see figure). On closing K2 also and adjusting R2 to 5 Ω, the deflection in galvanometer becomes θ0 / 5. The resistance of the galvanometer is, then, given by (neglect the internal resistance of battery) [2019]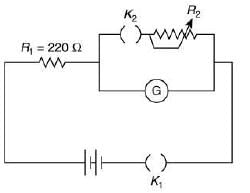
(1) 5 Ω
(2) 22 Ω
(3) 25 Ω
(4) 12 Ω
Ans: (2)
Let Rg is resistance of galvanometer
Case II(2)
⇒ 225Rg + 1100 = 5500 + 25Rg
⇒ 225Rg – 25Rg – 5500 – 1100
⇒ 200Rg = 4400
Q.22. A galvanometer, whose resistance is 50 Ω, has 25 divisions in it. When a current of 4 × 10−4 A passes through it, its needle (pointer) deflects by one division. To use this galvanometer as a voltmeter of range 2.5 V, it should be connected to a resistance of [2019]
(1) 250 Ω
(2) 200 Ω
(3) 6200 Ω
(4) 6250 Ω
Ans: (2)
Current flowing through galvanometer is Ig = 4 × 10–4 × 25
= 10−2 A
Now,
2.5 = (50 + R) × Ig [V = IR]
⇒ 2.5 = (50 + R) × 10−2
⇒ 2.5 × 102 = 50 + R
⇒ 250 = 50 + R
⇒ R = 200 Ω
Q.23. A bar magnet is demagnetized by inserting it inside a solenoid of length 0.2 m, 100 turns, and carrying a current of 5.2 A. The coercivity of the bar magnet is [2019]
(1) 285 A/m
(2) 2600 A/m
(3) 520 A/m
(4) 1200 A/m
Ans: (2)
Bar magnet requires a magnetic intensity μ.
The current through the solenoid is,
i = μ/n.
⇒ μ = i x n (1)
Let n be the turns per unit length.
Put this value in Eq. (1), we get
Q.24. A magnet of total magnetic moment 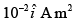 is placed in a time varying magnetic field,
is placed in a time varying magnetic field, 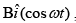 where B = 1 Tesla and ω = 0.125 rad/s. The work done for reversing the direction of the magnetic moment at t = 1 s, is [2019]
where B = 1 Tesla and ω = 0.125 rad/s. The work done for reversing the direction of the magnetic moment at t = 1 s, is [2019]
(1) 0.01 J
(2) 0.007 J
(3) 0.02 J
(4) 0.014 J
Ans: (3)
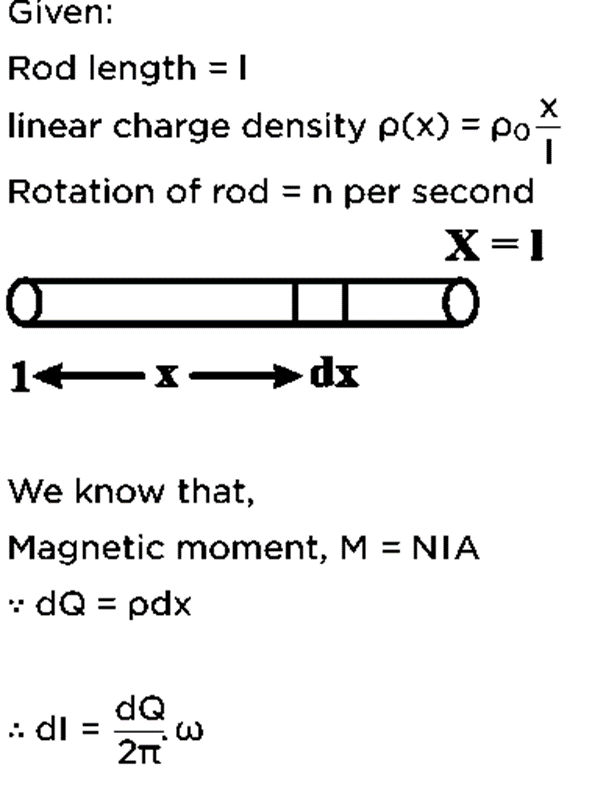
Q.25. An insulating thin rod of length l has a linear charge density 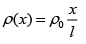 on it. The rod is rotated about an axis passing through the origin (x = 0) and perpendicular to the rod. If the rod makes n rotations per second, then the time-averaged magnetic moment of the rod is [2019]
on it. The rod is rotated about an axis passing through the origin (x = 0) and perpendicular to the rod. If the rod makes n rotations per second, then the time-averaged magnetic moment of the rod is [2019]
(1) πnρl3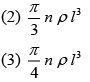
(4) nρl3
Ans: (3)
Q.26. A hoop and a solid cylinder of same mass and radius are made of a permanent magnetic material with their magnetic moment parallel to their respective axes. But the magnetic moment of hoop is twice of solid cylinder. They are placed in a uniform magnetic field in such a manner that their magnetic moments make a small angle with the field. If the oscillation periods of hoop and cylinder are Th and Tc respectively, then [2019]
(1) Th = Tc
(2) Th = 2Tc
(3) Th = 1.5Tc
(4) Th = 0.5Tc
Ans: (1)
Let μ be the magnetic moment, M masses of hoop and solid cylinder and R is the radius of hoop and solid cylinder.Oscillation period of hoop is
(1) [Th = MR2]
Oscillation period of cylinder is
Dividing Eq. (1) by Eq. (2), we get
Q.27. At some location on Earth, the horizontal component of Earth’s magnetic field is 18 × 10−6 T. At this location, magnetic needle of length 0.12 m and pole strength 1.8 A-m is suspended from its mid-point using a thread, it makes 45° angle with horizontal in equilibrium. To keep this needle horizontal, the vertical force that should be applied at one of its ends is [2019]
(1) 3.6 × 10−5 N
(2) 1.8 × 10−5 N
(3) 1.3 × 10−5 N
(4) 6.5 × 10−5 N
Ans: (4)
We have,.
FAQs on JEE Main Previous Year Questions (2016- 2025): Moving Charges & Magnetism- 1
| 1. What is the Biot-Savart Law and how is it applied in calculating magnetic fields due to current-carrying conductors? |  |
| 2. How do you determine the direction of the magnetic field around a current-carrying wire? |  |
| 3. What is the force experienced by a charged particle moving in a magnetic field? |  |
| 4. What is Ampère's Circuital Law and its significance in magnetism? |  |
| 5. How do you calculate the magnetic field at the center of a circular loop carrying current? |  |