Previous year questions (2016-2024): Properties of Triangle | JEE Main | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download

Q.1. With the usual notation, in ΔABC, if ∠A + ∠B = 120°, a = √3 +1 and b = √3 - 1, then the ratio ∠A : ∠B, is:    (2019)
(1) 7 : 1
(2) 5 : 3
(3) 9 : 7
(4) 3 : 1
Ans. (1)
Solution.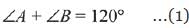




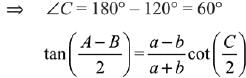
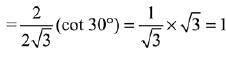
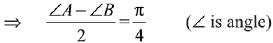
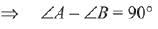  ...(2)
From eqn (1) and (2)
∠A = 105°, ∠B = 15°
Then, ∠A : ∠B = 7 : 1

Q.2. In a triangle, the sum of lengths of two sides is x and the product of the lengths of the same two sides is y. if x² - c² = y, where c is the length of the third side of the triangle, then the circumradius of the triangle is:    (2019)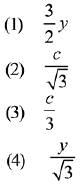

Ans. (2)
Solution.
Let two sides of triangle are a and b.
a + b = x
ab = y
x² - c² = y ⇒ (a + b)² - c² = ab
⇒ (a + b - c) (a + b + c) = ab
⇒ 2(s - c) (2s) = ab
⇒ 4s(s - c) = ab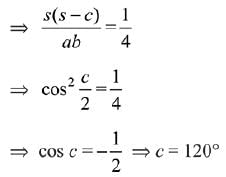

∴ Area of triangle is,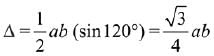

As,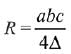
∴  

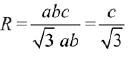
Q.3.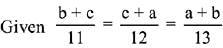 for a ΔABC with usual notation. If 

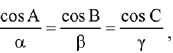 then the ordered triplet (α, β, γ) has a value:    (2019)
(1) (7, 19, 25)
(2) (3, 4, 5)
(3) (5, 12, 13)
(4) (19, 7, 25)
Ans. (1)
Solution.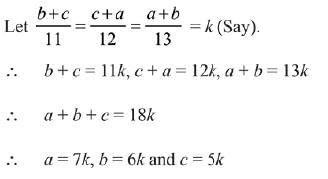



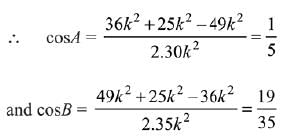
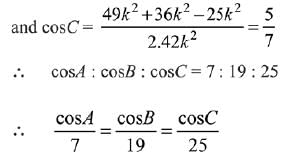
Hence, required ordered triplet is (7, 19, 25).

Q.4. If the lengths of the sides of a triangle are in A.P. and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is:    (2019)
(1) 5 : 9 : 13
(2) 4 : 5 : 6
(3) 3 : 4 : 5
(4) 5 : 6 : 7
Ans. (2)
Solution.
Let a,b,c are the sides in increasing order 2b = a + c
Let angles are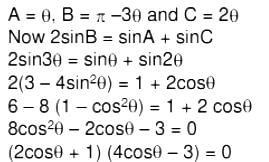


the ratio of sides a : b : c
sinA :sinB :sinC
sinθ : sin3θ : sin2θ
1 : 3 - 4sin²θ : 2cosθ
1 : 5/4 : 6/4 = 4 : 5 : 6

Q.5. The angles A, B and C of a triangle ABC are in A.P. and a : b= 1 : √3. If c = 4 cm, then the area (in sq.cm) of this triangle is:    (2019)
(1) 2/√3
(2) 4√3
(3) 2√3
(4) 4/√3
Ans. (3)
Solution.
Let the angles be a, a+d, a+2d
Then, a + a + d + a + 2d = 180º
= a + d = 60 = a + d = 60º
So angle B = 60º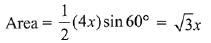



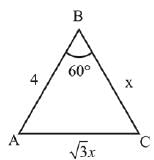
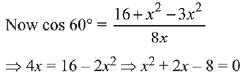
⇒ x = 2    [∵ x can't be negative]
Hence, area = 2√3 sq. cm

Q.6. PQR is a triangular park with PQ = PR = 200 m. A T.V. tower stands at the mid-point of QR. If the angle of elevation of the top of the tower at P,Q and R are respectively 45°, 30° and 30° then the height of tower (in m) is:    (2018)
(1) 100
(2) 50
(3) 100√3
(4) 50√2
Ans: (1)
Solution:

 


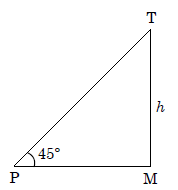
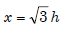
Now In ΔPOM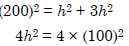

h = 100 meter

Q.7. An aeroplane flying at a constant speed, parallel to the horizontal ground, √3 km above it, is observed at an elevation of 60° from a point on the ground. If, after five seconds, its elevation from the same point, is 30°, then the speed (in km/hr) of the aeroplane, is:     (2018)
(1) 750
(2) 720
(3) 1440
(4) 1500
Ans: (3)
Solution:

Let from point C the angle of elevation of plane at B is 60º and after 5 seconds it reach at B'

Hence distance AA' = 2km


Q.8. A man on the top of a vertical tower observes a car moving at a uniform speed towards the tower on a horizontal road. If it takes 18 min. for the angle of depression of the car to change from 30° to 45° ; then after this, the time taken (in min.) by the car to reach the foot of the tower, is:    (2018)
(1)
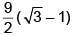
(2) 18(1 + √3)
(3) 18 (√3 – 1)
(4) 9 (1 + √3)
Ans: (4)
Solution:
Let length of tower = h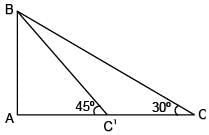

⇒ AC' = AB = h
and AC = AB cot 30º = √3 h
⇒ CC' = (√3 –1) h
Time taken by the car form C to C' = 18 min
⇒ time taken by the car to reach the foot of the tower =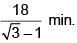
= 9 (√3 + 1) min

Q.9. The two adjacent sides of a cyclic quadrilateral are 2 and 5 and the angle between them is 60^o.
If the area of the quadrilateral is 4 √3 , then the perimeter of the quadrilateral is :    (2017)
(1) 12.5
(2) 13
(3) 13.2
(4) 12
Ans. (4)
Solution.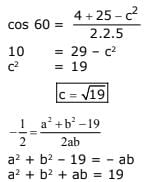

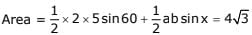
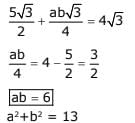
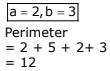
Q.10. A man is walking towards a vertical pillar in a straight path, at a uniform speed. At a certain point A on the path, he observes that the angle of elevation of the top of the pillar is 30°. After walking for 10 minutes from A in the same direction, at a point B, he observes that the angle of elevation of the top of the pillar is 60°. Then the time taken (in minutes) by him, from B to reach the pillar, is:    (2016)
(1) 6
(2) 10
(3) 20
(4) 5
Ans. (4)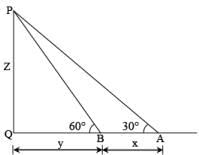

Let AB = x, BQ = y, PQ = z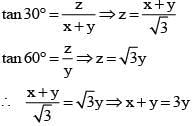

x = 2y
∴ y =x/2
To go x, it takes 10 minutes.
∴ To go y, it takes 5 minutes.

Q.11. The angle of elevation of the top of a vertical tower from a point A, due east of it is 45º. The angle of elevation of the top of the same tower from a point B, due south of A is 30º. If the distance between A and B is 54 √2 m, then the height of the tower (in metres), is    (2016)
(1) 54
(2) 108
(3) 54√3
(4) 36√3
Ans. (1)
Let height of tower is h.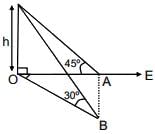

⇒ OA = G
OB = √3 h
Also OB² = OA² + AB²
⇒ 3h² = h² + (54√2 )² ⇒ h = 54