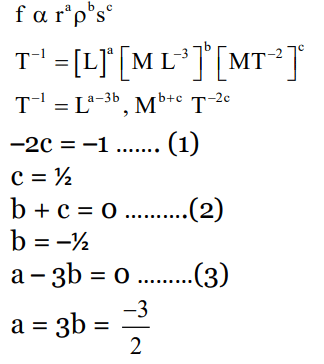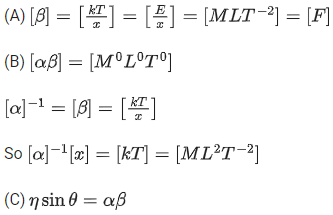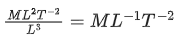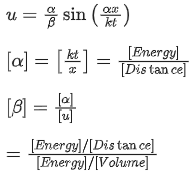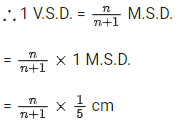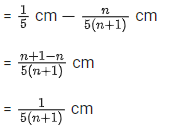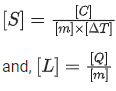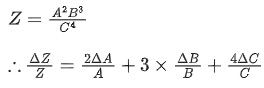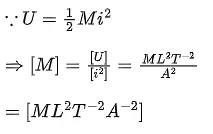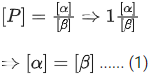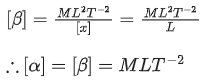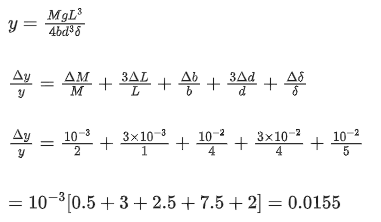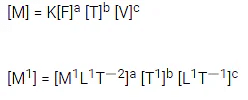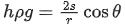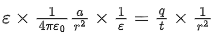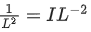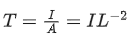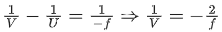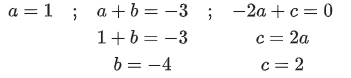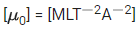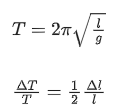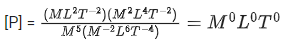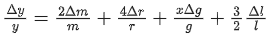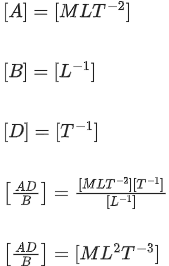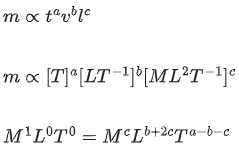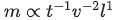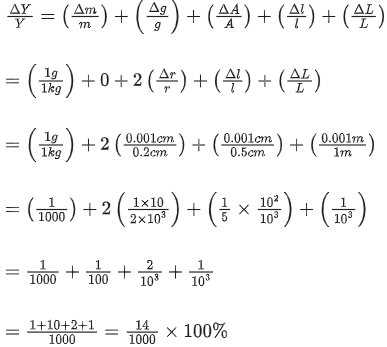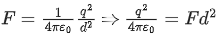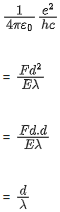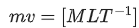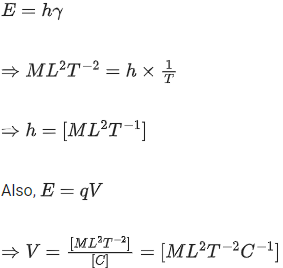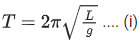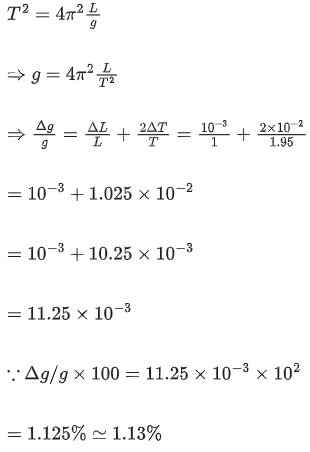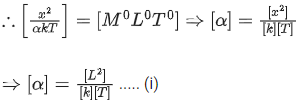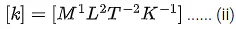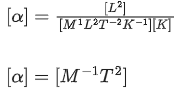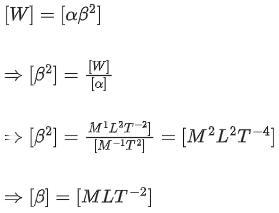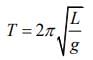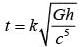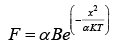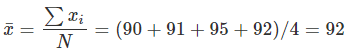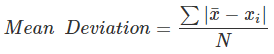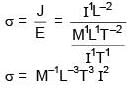JEE Main Previous Year Questions (2016- 2024): Units & Measurements PDF Download

Q.1. Match List I with List II      [(JEE Main 2023)]

Choose the correct answer from the options given below:

(1) A-I, B-III, C-IV, D-II 
(2) A-III, B-I, C-II, D-IV 
(3) A-II, B-IV, C-III, D-I 
(4) A-III, B-IV, C-I, D-II 

Correct Answer is Option (4)
Solution: 

Q.2. The frequency (𝑣) of an oscillating liquid drop may depend upon radius (𝑟) of the drop, density (𝜌) of liquid and the surface tension (s) of the liquid as : 𝑣 = 𝑟^a𝜌^bs^c. The values of a, b and c respectively are:         [(JEE Main 2023)]

Correct Answer is Option (3)
Solution: 

Q.3. Match List I with List II             [(JEE Main 2023)]

Choose the correct answer from the options given below:
(1) A-II , B-I , C-III , D-IV 

(2) A-IV, B-III , C-I , D-II

(3) A-III , B-IV, C-I , D-II 

(4) A-IV , B-III , C-II , D-I

Correct Answer is Option (2)
Solution: 

Q.4. Match List I with List II             [(JEE Main 2023)]

Choose the correct answer from the options given below options:

(1) A-I, B-II, C-III, D-IV 

(2) A-II, B-III, C-IV, D-I

(3) A-I, B-III, C-IV, D-II 

(4) A-III, B-I, C-II, D-IV

Correct Answer is Option (4)

Solution:

Q.5. Match List I with List II:

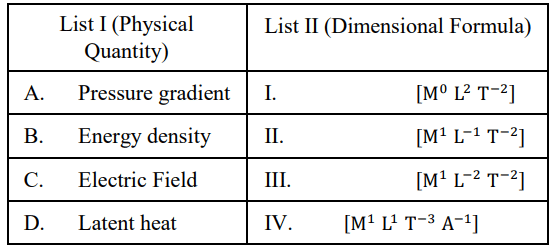
Choose the correct answer from the options given below:

(1) A-II, B – III, C-I, D-IV 

(2) A-II, B – III, C-IV, D-I

(3) A-III, B – II, C-IV, D-I 

(4) A-III, B – II, C-I, D-IV

Correct Answer is Option (3)

Solution: 

Q.6. Match List I with List II.     [(JEE Main 2022)]
Choose the correct answer from the options given below:
(a) A-III, B-II, C-I, D-IV
(b) A-III, B-IV, C-II, D-I
(c) A-IV, B-I, C-III, D-II
(d) A-II, B-III, C-I, D-IV

Correct Answer is Option (b)
Solution: 

• Torque → Nm
  Torque (measured in Newton-meters or Nm) is a physical quantity that represents the rotational force applied to an object. It is the product of the force applied to the object and the distance from the point of rotation at which the force is applied.

Torque

• Stress → N/m^{2
  Stress (measured in Newton per square meter or N/m^2), also known as pressure, is a physical quantity that describes the internal forces experienced by a material when subjected to external forces. It is calculated by dividing the force applied to an object by its cross-sectional area.}
• Latent heat → J/kg
  Latent heat (measured in Joules per kilogram or J/kg) is a physical quantity that represents the amount of energy absorbed or released by a substance during a phase change (such as solid to liquid or liquid to gas) at a constant temperature. It is the heat energy per unit mass required to change the phase of a substance without changing its temperature.
• Power → Nm/s
  Power (measured in Newton-meters per second or Nm/s), in the context of physics, represents the rate at which work is done or energy is transferred. It is the product of force and velocity, or the rate at which torque is applied. It quantifies how quickly energy is being transformed or transferred from one form to another.

Q.7. In an experiment to find out the diameter of wire using screw gauge, the following observations were noted :     [(JEE Main 2022)]

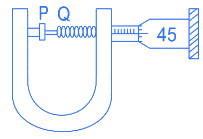(A) Screw moves 0.5 mm on main scale in one complete rotation
(B) Total divisions on circular scale =50
(C) Main scale reading is 2.5 mm
(D) 45^th  division of circular scale is in the pitch line
(E) Instrument has 0.03 mm negative error
Then the diameter of wire is:
(a) 2.92 mm
(b) 2.54 mm
(c) 2.98 mm
(d) 3.45 mm

Correct Answer is Option (c)
Solution: 

Least count =pitch/number of divisions on circular scale

L.C. = 0.5 / 50 mm = 0.01 mm

Measured diameter = (main scale reading) + (circular scale reading ) ( least count )

=2.5 mm  + (45) (0.01 mm) =2.95 mm
Actual diameter = measured diameter - zero error

2.95 mm−(−0.03 mm)
= 2.98 mm

Q.8. A travelling microscope has 20 divisions per cm on the main scale while its vernier scale has total 50 divisions and 25 vernier scale divisions are equal to 24 main scale divisions, what is the least count of the travelling microscope?     [(JEE Main 2022)]
(a) 0.001 cm
(b) 0.002 mm
(c) 0.002 cm
(d) 0.005 cm

Correct Answer is Option (c)
Solution: 
1 MSD = 1/20 cm
1 VSD = 24/25 × 1/20 cm
∴ Least count = 1 MSD − 1 VSD
= 1/20(1 − 24/25) cm
= 1/20 × 1/25 cm
= 0.002 cm

Q.9. Consider the efficiency of carnot's engine is given by 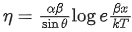, where α and β are constants. If T is temperature, k is Boltzmann constant, θ is angular displacement and x has the dimensions of length. Then, choose the incorrect option:     [(JEE Main 2022)] 
(a) Dimensions of β is same as that of force.
(b) Dimensions of α⁻¹x is same as that of energy.
(c) Dimensions of η⁻¹sin⁡θ is same as that of αβ
(d) Dimensions of α is same as that of β.

Correct Answer is Option (d)
Solution: 

So [ηsin⁡θ] = [αβ]
[η] = [M⁰L⁰T⁰] it is dimensionless quantity
(D) [α] ≠ [β]

Q.10. The dimensions of 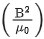 will be :
(if μ₀  : permeability of free space and  : magnetic field)     [(JEE Main 2022)]
(a) [ML²T⁻²]
(b) [MLT⁻²]
(c) [ML⁻¹ T⁻²]
(d) [ML² T⁻² A⁻¹]

Correct Answer is Option (c)
Solution: 
 = [Energy density]
=

Q.11. An expression of energy density is given by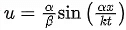, where α,β are constants, x is displacement, k is Boltzmann constant and t is the temperature. The dimensions of β will be     [(JEE Main 2022)]
(a) [ML² T⁻²θ⁻¹]
(b) [M⁰ L² T⁻²]
(c) [M⁰ L⁰ T⁰]
(d) [M⁰ L² T⁰]

Correct Answer is Option (d)
Solution: 

= [L²]

Q.12. A torque meter is calibrated to reference standards of mass, length and time each with 5% accuracy. After calibration, the measured torque with this torque meter will have net accuracy of:     [(JEE Main 2022)]
(a) 15%
(b) 25%
(c) 75%
(d) 5%

Correct Answer is Option (b)
Solution:

= 5 x 5% = 25%

Q.13. In a Vernier Calipers, 10 divisions of Vernier scale is equal to the 9 divisions of main scale. When both jaws of Vernier calipers touch each other, the zero of the Vernier scale is shifted to the left of zero of the main scale and 4^th Vernier scale division exactly coincides with the main scale reading. One main scale division is equal to 1 mm. While measuring diameter of a spherical body, the body is held between two jaws. It is now observed that zero of the Vernier scale lies between 30 and 31 divisions of main scale reading and 6^th Vernier scale division exactly coincides with the main scale reading. The diameter of the spherical body will be :     [(JEE Main 2022)]
(a) 3.02 cm
(b) 3.06 cm
(c)  3.10 cm
(d)  3.20 cm

Correct Answer is Option (c)
Solution: 
10 VSD = 9 MSD
⇒LC = 1/10MSD = 0.01 cm
Negative error = (0.1 − 0.04) cm = 0.06 cm
Reading = (3.0 cm) + 6(0.01) cm + 0.06 cm
= 3.12 cm
Closer to 3.10 cm

Q.14. A screw gauge of pitch 0.5 mm is used to measure the diameter of uniform wire of length 6.8 cm, the main scale reading is 1.5 mm and circular scale reading is 7 . The calculated curved surface area of wire to appropriate significant figures is :     [(JEE Main 2022)]
[Screw gauge has 50 divisions on its circular scale]
(a) 6.8 cm²
(b) 3.4 cm²
(c) 3.9 cm²
(d) 2.4 cm²

Correct Answer is Option (b)
Solution: 
Least count = 0.5/50 mm = 0.01 mm
∴ Diameter, d = 1.5 mm + 7 × 0.01
= 1.57 mm
∴ Surface area =(2πr) × l
= πdl
= 3.142 × 1.57/10 × 6.8 cm²
= 3.354 cm² = 3.4 cm²

Q.15. The maximum error in the measurement of resistance, current and time for which current flows in an electrical circuit are 1%,2% and 3% respectively. The maximum percentage error in the detection of the dissipated heat will be:     [(JEE Main 2022)]
(a) 2
(b) 4
(c) 6
(d) 8

Correct Answer is Option (d)
Solution: 
∵ H = i²Rt
∵ % error in H = 2 × 2% + 1% + 3%
= 8%

Q.16. If momentum [P], area [A] and time [T] are taken as fundamental quantities, then the dimensional formula for coefficient of viscosity is :     [(JEE Main 2022)]
(a) [PA⁻¹ T⁰]
(b) [PA T⁻¹]
(c) [PA⁻¹ T]
(d) [PA⁻¹ T⁻¹]

Correct Answer is Option (a)
Solution: 

Q.17. If n main scale divisions coincide with (n + 1) vernier scale divisions. The least count of vernier callipers, when each centimetre on the main scale is divided into five equal parts, will be :     [(JEE Main 2022)]
(a) 2/n+1 mm
(b) 5/n+1 mm
(c) 1/2n mm
(d) 1/5n mm

Correct Answer is Option (a)
Solution: 
5 parts of main scale division = 1 cm
∴ 1 part of main scale division = 1/5 cm
∴ 1 M.S.D. = 1/5 cm
(n + 1) vernier scale division = n main scale division.

We know,
L.C. = 1 M.S.D. − 1 V,S.D.

Q.18. Identify the pair of physical quantities which have different dimensions:     [(JEE Main 2022)]
(a) Wave number and Rydberg's constant
(b) Stress and Coefficient of elasticity
(c) Coercivity and Magnetisation
(d) Specific heat capacity and Latent heat

Correct Answer is Option (d)
Solution: 

⇒ They have different dimensions.

Q.19. Identify the pair of physical quantities that have same dimensions:     [(JEE Main 2022)]
(a) velocity gradient and decay constant
(b) Wien's constant and Stefan constant
(c) angular frequency and angular momentum
(d) wave number and Avogadro number

Correct Answer is Option (a)
Solution: 
Velocity gradient = dv/dx
⇒ Dimensions are [LT⁻¹] / [L]  = [T⁻¹]
Decay constant λ has dimensions of [T⁻¹] because of the relation dN / dt=−λ N
⇒ Velocity gradient and decay constant have same dimensions.

Q.20. If Z=A²B³ / C⁴, then the relative error in Z will be :     [(JEE Main 2022)]
(a)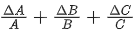
(b)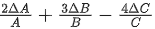
(c)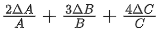
(d)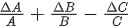

Correct Answer is Option (c)
Solution: 

Q.21. The dimension of mutual inductance is :     [(JEE Main 2022)]
(a) [ML²T⁻²A⁻¹]
(b) [ML²T⁻³A⁻¹]
(c) [ML²T⁻²A⁻²]
(d) [ML²T⁻³A⁻²]

Correct Answer is Option (c)
Solution: 

Q.22. An expression for a dimensionless quantity P is given by 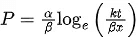; where α and β are constants, x is distance; k is Boltzmann constant and t is the temperature. Then the dimensions of α will be :     [(JEE Main 2022)]
(a) [M⁰ L⁻¹ T⁰]
(b) [M L⁰ T⁻²]
(c) [M L T⁻²]
(d) [M L² T⁻²]

Correct Answer is Option (c)
Solution: 

Now, [kt / βt] = 1
We know, E = 3/2kT(KTG)
∴ [Energy] = [KT]

Q.23. A silver wire has a mass (0.6 ± 0.006) g, radius (0.5 ± 0.005) mm and length (4 ± 0.04) cm. The maximum percentage error in the measurement of its density will be :     [(JEE Main 2022)]
(a) 4%
(b) 3%
(c) 6%
(d) 7%

Correct Answer is Option (a)
Solution: 

= 4%

Q.24. The SI unit of a physical quantity is pascal-second. The dimensional formula of this quantity will be:     [(JEE Main 2022)]
(a) [ML⁻¹T⁻¹]
(b) [ML⁻¹T⁻²
(c) [ML²T⁻¹]
(d) [M⁻¹L³T⁰]

Correct Answer is Option (a)
Solution:
[pascal-second] = MLT⁻² / L² × T
[ML⁻¹T⁻¹]

Q.25. Area of the cross-section of a wire is measured using a screw gauge. The pitch of the main scale is 0.05 mm. The circular scale has 100 divisions and for one full rotation of the circular scale, the main scale shifts by two divisions. The measured readings are listed below.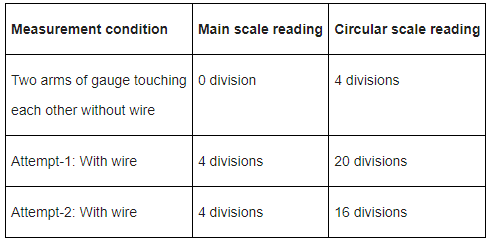
What are the diameter and cross-sectional area of the wire measured using the screw gauge?     [(JEE Advance 2022)]
(a) 2.22 ± 0.02 mm, π(1.23 ± 0.02)mm²
(b) 2.22 ± 0.01 mm, π(1.23 ± 0.01)mm²
(c) 2.14 ± 0.02 mm, π(1.14 ± 0.02)mm²
(d) 2.14 ± 0.01 mm, π(1.14 ± 0.01)mm²

Correct Answer is Option (c)

Q.26. A student determined Young's Modulus of elasticity using the formula 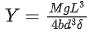. The value of g is taken to be 9.8 m/s2, without any significant error, his observation are as following.      [(JEE Mains 2021)]
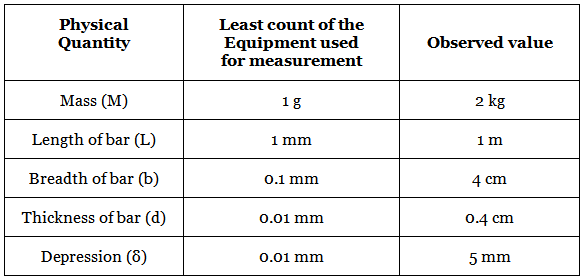Then the fractional error in the measurement of Y is :
(a) 0.0083
(b) 0.0155
(c) 0.155
(d) 0.083

Correct Answer is Option (b)
Solution: 

Q.27. If velocity [V], time [T] and force [F] are chosen as the base quantities, the dimensions of the mass will be :      [(JEE Mains 2021)]
(a) [FT⁻¹ V⁻¹]
(b) [FTV⁻¹]
(c) [FT² V]
(d) [FVT⁻¹]

Correct Answer is Option (b)
Solution: 

a = 1, b = 1, c = −1
∴ [M] = [FTV⁻¹]

Q.28. Which of the following equations is dimensionally incorrect?
Where t = time, h = height, s = surface tension, θ = angle, ρ = density, a, r = radius, g = acceleration due to gravity, v = volume, p = pressure, W = work done, T = torque, ∈ = permittivity, E = electric field, J = current density, L = length.      [(JEE Mains 2021)]
(a)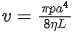
(b)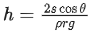
(c)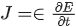
(d) W = Tθ

Correct Answer is Option (a)
Solution: 
(a)  = = Volumetric flow rate (Poiseuille's law) 
(b)
(c)
=
LHS

(d) W = Tθ

Q.29. Match List - I with List - II.      [(JEE Mains 2021)]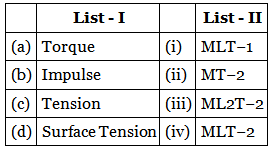

Choose the most appropriate answer from the option given below:
(a) (a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)
(b) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
(c) (a)-(i), (b)-(iii), (c)-(iv), (d)-(ii)
(d) (a)-(iii), (b)-(iv), (c)-(i), (d)-(ii)

Correct Answer is Option (a)
Solution: 
torque τ → ML²T⁻² (iii)
Impulse I → MLT⁻¹ (i)
Tension force → MLT⁻² (iv)
Surface tension → MT⁻² (ii)

Q.30. An object is placed at the focus of concave lens having focal length f. What is the magnification and distance of the image from the optical centre of the lens?      [(JEE Mains 2021)]
(a) 1, ∞
(b) Very high, ∞
(c) 1/2, f/2
(d) 1/4, f/4

Correct Answer is Option (c)
Solution: 

U = −f

V = −f / 2
m = VU = 1 / 2
distance = f / 2

Q.31. If force (F), length (L) and time (T) are taken as the fundamental quantities. Then what will be the dimension of density:      [(JEE Mains 2021)]
(a) [FL−4T2]
(b) [FL−3T2]
(c) [FL−5T2]
(d) [FL−3T3]

Correct Answer is Option (a)
Solution:
Density = [F^aL^bT^c]
[ML⁻³] = [M^aL^a+bT^−2aLbTc]
[M¹L⁻³] = [M^aL^a+bT^−2a+c]

So, density = [F¹L⁻⁴T²]

Q.32. Match List - I with List - II.      [(JEE Mains 2021)]
Choose the most appropriate answer from the options given below :
(a) (a)-(ii), (b)-(iii), (c)-(iv), (d)-(i)
(b) (a)-(iii), (b)-(ii), (c)-(iv), (d)-(i)
(c) (a)-(iv), (b)-(ii), (c)-(i), (d)-(iii)
(d) (a)-(iii), (b)-(ii), (c)-(i), (d)-(iv)

Correct Answer is Option (b)
Solution: 
SI unit of Rydberg const. = m⁻¹
SI unit of Plank's const. = kg m²s⁻¹
SI unit of Magnetic field energy density = kg m⁻¹s⁻²
SI unit of coeff. of viscosity = kg m⁻¹s⁻¹

Q.33. If E and H represents the intensity of electric field and magnetising field respectively, then the unit of E/H will be:      [(JEE Mains 2021)]
(a) ohm
(b) mho
(c) joule
(d) newton

Correct Answer is Option (a)
Solution: 
Units of E/H is volt/meter / Ampere / meter = Volt/Ampere = ohm

Q.34. Which of the following is not a dimensionless quantity?      [(JEE Mains 2021)]
(a) Relative magnetic permeability (μ_r)
(b) Power factor
(c) Permeability of free space (μ₀)
(d) Quality factor

Correct Answer is Option (c)
Solution: 

[power factor (cos ϕ)] = 1
  : Not dimensionless

quality factor (Q)=Energy stored / Energy dissipated per cycle
So Q is unitless & dimensionless.

Q.35. If the length of the pendulum in pendulum clock increases by 0.1%, then the error in time per day is:      [(JEE Mains 2021)]
(a) 86.4 s
(b) 4.32 s
(c) 43.2 s
(d) 8.64 s

Correct Answer is Option (c)
Solution: 

ΔT = 1/2 × 0.1 / 100 × 24 × 3600
ΔT= 43.2

Q.36. Match List - I with List - II      [(JEE Mains 2021)]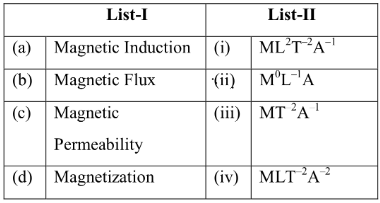
Choose the most appropriate answer from the options given below:
(a) (a)-(ii), (b)-(iv), (c)-(i), (d)-(iii)
(b) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
(c) (a)-(iii), (b)-(ii), (c)-(iv), (d)-(i)
(d) (a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)

Correct Answer is Option (d)
Solution:
(a) Magnetic Induction = MT⁻²A−1
(b) Magnetic Flux = ML²T⁻²A⁻¹
(c) Magnetic Permeability = MLT⁻²A⁻²
(d) Magnetization = M⁰L⁻¹A

Q.37. If E, L, M and G denote the quantities as energy, angular momentum, mass and constant of gravitation respectively, then the dimensions of P in the formula P = EL²M⁻⁵G⁻² are :      [(JEE Mains 2021)]
(a) [M⁰ L¹ T⁰]
(b) [M⁻¹ L⁻¹ T²]
(c) [M¹ L¹ T⁻²]
(d) [M⁰ L⁰ T⁰]

Correct Answer is Option (d)
Solution: 
E = ML²T⁻²
L = ML²T⁻¹
m = M
G = M⁻¹L+3T⁻²

Q.38. In a Screw Gauge, fifth division of the circular scale coincides with the reference line when the ratchet is closed. There are 50 divisions on the circular scale, and the main scale moves by 0.5 mm on a complete rotation. For a particular observation the reading on the main scale is 5 mm and the 20th division of the circular scale coincides with reference line. Calculate the true reading.      [(JEE Mains 2021)]
(a) 5.00 mm
(b) 5.25 mm
(c) 5.15 mm
(d) 5.20 mm

Correct Answer is Option (c)
Solution:
Least count (L. C.) = 0.5 / 50
True reading = 5 + 0.5 / 50  x 20 − 0.5 / 50 × 5
= 5 + 0.5 / 50(15) = 5.15 mm

Q.39. A physical quantity 'y' is represented by the formula 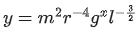If the percentage errors found in y, m, r, l and g are 18, 1, 0.5, 4 and p respectively, then find the value of x and p.      [(JEE Mains 2021)]
(a) 5 and ±2
(b) 4 and ±3
(c) 163 and ±32
(d) 8 and ± 2

Correct Answer is Option (c)
Solution: 

18 = 2(1) + 4(0.5) + xp + 3 / 2(4)
⇒ 8 = xp
By checking from options.
x = 16 / 3, p = ±3 / 2

Q.40.  Assertion A : If in five complete rotations of the circular scale, the distance travelled on main scale of the screw gauge is 5 mm and there are 50 total divisions on circular scale, then least count is 0.001 cm.      [(JEE Mains 2021)]
Reason R :
Least Count = Pitch / Total divisions on circular scale
In the light of the above statements, choose the most appropriate answer from the options given below :
(a) A is not correct but R is correct.
(b) Both A and R are correct and R is the correct explanation of A.
(c) A is correct but R is not correct.
(d) Both A and R are correct and R is NOT the correct explanation of A.

Correct Answer is Option (a)
Solution: 
Least Count = Pitch / Total divisions on circular scale
In 5 revolution, distance travel, 5 mm
In 1 revolution, it will travel 1 mm.
So least count = 1 / 50 = 0.02

Q.41. The force is given in terms of time t and displacement x by the equation
F = A cos Bx + C sin Dt      [(JEE Mains 2021)]
The dimensional formula of AD / B is :
(a) [M⁰LT⁻¹]
(b) [ML²T⁻³]
(c) [M¹L¹T⁻²]
(d) [M²L²T⁻³]

Correct Answer is Option (b)
Solution: 

Q.42. If time (t), velocity (v), and angular momentum (l) are taken as the fundamental units. Then the dimension of mass (m) in terms of t, v and l is :      [(JEE Mains 2021)]
(a)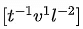
(b)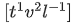
(c)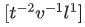
(d)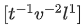

Correct Answer is Option (d)
Solution: 

comparing powers
c = 1, b = −2, a = −1

Q.43. The vernier scale used for measurement has a positive zero error of 0.2 mm. If while taking a measurement it was noted that '0' on the vernier scale lies between 8.5 cm and 8.6 cm, vernier coincidence is 6, then the correct value of measurement is ___________ cm. (least count = 0.01 cm)      [(JEE Mains 2021)]
(a) 8.58 cm
(b) 8.54 cm
(c) 8.56 cm
(d) 8.36 cm

Correct Answer is Option (b)
Solution: 
Reading = MSR + VSD × LC − zero error
Reading = 8.5 + (0.1) × 6 / 10 − 0.2 / 10 = 8.54 cm

Q.44. In order to determine the Young's Modulus of a wire of radius 0.2 cm (measured using a scale of least count = 0.001 cm) and length 1m (measured using a scale of least count = 1 mm), a weight of mass 1 kg (measured using a scale of least count = 1 g) was hanged to get the elongation of 0.5 cm (measured using a scale of least count 0.001 cm). What will be the fractional error in the value of Young's Modulus determined by this experiment?      [(JEE Mains 2021)]
(a) 0.14%
(b) 9%
(c) 1.4%
(d) 0.9%

Correct Answer is Option (c)
Solution: 

= 1.4%

Q.45. One main scale division of a vernier callipers is 'a' cm and nth division of the vernier scale coincide with (n − 1)^th division of the main scale. The least count of the callipers in mm is :      [(JEE Mains 2021)]
(a)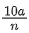
(b)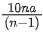
(c)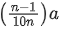
(d)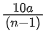

Correct Answer is Option (a)
Solution: 
n VSD = (n − 1) MSD
1 VSD = (n−1 / n)MSD
L.C. = 1 MSD − 1 VSD
= 1 MSD − (n− / n)MSD
= 1 MSD − 1 MSD + MSD / n
= MSD / n
= a / n cm
= 10a / n mm

Q.46. If 'C' and 'V' represent capacity and voltage respectively then what are the dimensions of λ where C/V = λ ?      [(JEE Mains 2021)]
(a) [M⁻³L⁻⁴I³T⁷]
(b) [M⁻²L−3I²T⁶]
(c) [M⁻²L⁻⁴I³T⁷]
(d) [M⁻¹L⁻³I⁻²T⁻⁷]

Correct Answer is Option (c)
Solution: 

Q.47. In a typical combustion engine the workdone by a gas molecule is given by 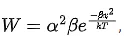 where x is the displacement, k is the Boltzmann constant and T is the temperature. If α and β are constants, dimensions of α will be :      [(JEE Mains 2021)]
(a) [M⁰LT⁰]
(b) [MLT⁻¹]
(c) [MLT⁻²]
(d) [M²LT⁻²]

Correct Answer is Option (a)
Solution: 
kT has dimension of energy
βx² / kT is dimensionless
[β][L²]  = [ML²T⁻²]
[β] = [MT⁻²]
α²β has dimensions of work
[α²][MT⁻²] = [ML²T⁻²]

Q.48. If e is the electronic charge, c is the speed of light in free space and h is Planck's constant, the quantity 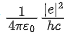 has dimensions of :      [(JEE Mains 2021)]
(a) [MLT⁻¹]
(b) [MLT⁰]
(c) [M⁰L0T⁰]
(d) [LC⁻¹]

Correct Answer is Option (c)
Solution: 
Given
e = electronic charge
c = speed of light in free space
h = Planck's constant
We know, E = hc / λ
and


= dimensionless
= [M⁰L0T⁰]

Q.49. The pitch of the screw gauge is 1 mm and there are 100 divisions on the circular scale. When nothing is put in between the jaws, the zero of the circular scale lies 8 divisions below the reference line. When a wire is placed between the jaws, the first linear scale division is clearly visible while 72nd division on circular scale coincides with the reference line. The radius of the wire is :      [(JEE Mains 2021)]
(a) 1.80 mm
(b) 0.90 mm
(c) 0.82 mm
(d) 1.64 mm

Correct Answer is Option (c)
Solution: 
Least count = 1mm / 100  = 0.01mm
zero error = + 8 × LC = + 0.08 mm
True reading (Diameter)
= (1 mm + 72 × LC) − (Zero error)
= (1 mm + 72 × 0.01 mm) − 0.08 mm
= 1.72 mm − 0.08 mm
= 1.64 mm
Therefore, radius = 1.64 / 2 = 0.82 mm.

Q.50. Match List - I with List - II :      [(JEE Mains 2021)]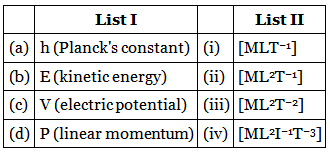
Choose the correct answer from the options given below :
(a) (a) → (ii), (b) → (iii), (c) → (iv), (d) → (i)
(b) (a) → (i), (b) → (ii), (c) → (iv), (d) → (iii)
(c) (a) → (iii), (b) → (ii), (c) → (iv), (d) → (i)
(d) (a) → (iii), (b) → (iv), (c) → (ii), (d) → (i)

Correct Answer is Option (a)
Solution: 
Kinetic Energy,

Momentum,

Plank constant :

Q.51. The period of oscillation of a simple pendulum is . Measured value of 'L' is 1.0 m from meter scale having a minimum division of 1 mm and time of one complete oscillation is 1.95 s measured from stopwatch of 0.01 s resolution. The percentage error in the determination of 'g' will be :      [(JEE Mains 2021)]
(a) 1.30%
(b) 1.33%
(c) 1.13%
(d) 1.03%

Correct Answer is Option (c)
Solution: 
Given,

where, time period, T = 1.95 s
Length of string, l = 1 m
Acceleration due to gravity = g
Error in time period, ΔT = 0.01 s = 10⁻² s
Error in length, ΔL = 1 mm = 1 × 10⁻³ m
Squaring Eq. (i) on both sides, we get

Q.52. The work done by a gas molecule in an isolated system is given by, 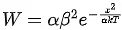, where x is the displacement, k is the Boltzmann constant and T is the temperature. α and β are constants. Then the dimensions of β will be :      [(JEE Mains 2021)]
(a) [M⁰LT⁰]
(b) [ML²T⁻²]
(c) [MLT⁻²]
(d) [M²LT²]

Correct Answer is Option (c)
Solution: 
where, k is Boltzmann constant,
T is temperature and x is displacement.
We know that, x² / αkT is a dimensionless quantity.

Since, dimensions of k are

Dimensions of temperature are
[T] = [K] ..... (iii)
Substituting Eqs. (ii) and (iii) in Eq. (i), we get

According to dimensional analysis,

Q.53. The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is     [(JEE Advance 2021)]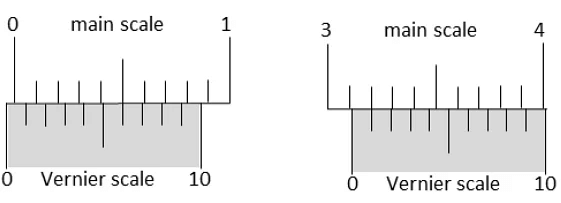
(a) 3.07 cm
(b) 3.11 cm
(c) 3.15 cm
(d) 3.17 cm

Correct Answer is Option (c)
Solution: 
Least count of Vernier calipers (L.C) = (1−9 / 10)0.1 = 0.01 cm
We know that main scale reading (MSR) is the first reading on the main scale immediately to the left of the zero of the Vernier scale. But there are no marks on the main scale before zero of the Vernier scale. We claim that MSR = −0.1 cm. The Vernier scale reading is VSR = 6 and the least count is LC = 0.01 cm.
Substitute these values to get,
Zero Error = MSR + VSR × LC
= -0.1 + 6 × 0.01 = -0.04 cm
Now in the second figure, the reading from main scale is 3.1 cm will be added to 1st matching division of vernier so,
Reading = 3.1 cm + 1 × L.C
= 3.1 cm + 0.01
= 3.11 cm
So correct diameter of the sphere
= 3.11 - (Zero Error)
= (3.11 + 0.04) cm
= 3.15 cm

Q.54. The dimensions of B²/2μ₀, where B is magnetic field and μ₀ is the magnetic permeability of vacuum, is     [(JEE Main 2020)]
(a) [MLT⁻²]
(b) [ML²T⁻¹]
(c) [ML²T⁻²]
(d) [ML⁻¹T⁻²]

Correct Answer is Option (d)
Solution:
The given quantity is energy density of magnetic field.
ε = E/V = B²/2μ₀
So, dimension is given by
[B²/2μ₀] = [ML²T²/L³] = [ML^-1T^-2]

Q.55. The dimensions of stopping potential V₀ in photoelectric effect in the units of Planck’s constant ‘h’, speed of light ‘c’ and Gravitational constant ‘G’ and ampere 'A' is    [(JEE Main 2020)]
(a) h^1/3G^2/3 c^1/3A^-1
(b) h^2/3G^5/3 c^1/3 A^-1
(c) h^-2/3c^-1/3G^4/3A^-1
(d) h² G^3/2 c^1/3 A^-1

Correct Answer is Option (None)
Solution:
We have
v₀ = h^wc^xG^yA^z
We know that
V₀ = [ML²T^-3A^-1], h = [ML²T^-1]
c = [LT^-1], G = [M^-1L³T^-2], I = [A]
So,
[ML²T^-3A^-1] = [ML²T^-1]^w[LT^-1]^x[M^-1L³T^-2]^y[A]^z
⇒ [ML²T^-3A^-1] = [M^w-yL^2w+x+3yT^-w-x-2yA^z]
⇒ w - y = 1, 2w + x + 3y = 2, -w-x-2y = -3, z = -1
Solving the equations, we get
w = 0, x = 5, y = -1, z = -1
Therefore,
V₀ = h⁰c⁵G^-1A^-1

Q.56. A simple pendulum is being used to determine the value of gravitational acceleration g at a certain place. The length of the pendulum is 25.0 cm and a stopwatch with 1s resolution measures the time taken for 40 oscillations to be 50 s. The accuracy in measurement of g is    [(JEE Main 2020)]
(a) 5.40%
(b) 3.40%
(c) 4.40%
(d) 2.40% 

Correct Answer is Option (c)
Solution: 
Given that
L = 25cm, Δt = 1s, n = 40, t= 50s
Time period of simple pendulum is given by

⇒ g = 4π²L/t²
⇒ Δg/g = (ΔL/L + 2Δt/t) = (0.1/25.0) + (2 x 1/50) = (1.1/25)
⇒ (Δg/g) x 100% = 4.4%

Q.57. A quantity f is given by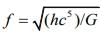 
 
where 'c' is speed of light, 'G' universal gravitational constant and 'h' is the Planck’s constant. Dimension of f is that of    [(JEE Main 2020)]
(a) Area
(b) Energy
(c) Momentum
(d) Volume

Correct Answer is Option (b)
Solution: 
Given that
  
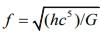
We know that
h = [ML²T^-1]
c = [LT^-1]
G = [M^-1L³T^-2]
So,
f = [ML²T^-1]^1/2[LT^-1]^5/2[M^-1L³T^-2]^-1/2
= [M^1/2+1/2L^2/2+5/2-3/2T^-1/2-5/2+2/2] = [M¹L²T^-2]
The dimension is equal to energy dimension.

Q.58. If the screw on a screw-gauge is given six rotations, it moves by 3 mm on the main scale. If there are 50 divisions on the circular scale, the least count of the screw gauge is     [(JEE Main 2020)]
(a) 0.001 mm
(b) 0.02 mm
(c) 0.01 cm
(d) 0.001 cm

Correct Answer is Option (a)
Solution: 
Given that
6 rotations = 3 mm MSR (Main Scale Reading)
⇒ 1 rotation = 1/2 mm = 0.5 mm
Number of divisions in circular scale = 50 divisions
Least count of screw-gauge is given by
LC = (MSR in 1 rotation/circular division) = 0.5/50 mm = 0.001mm

Q 59. Four sets of three measured physical quantities are given below. Which of the following options is correct?     [(JEE Main 2020)]
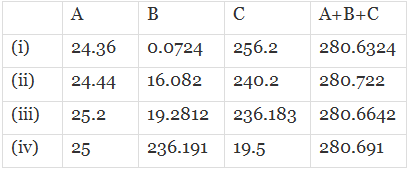
(i) A₁ = 24.36, B₁ = 0.0724, C₁ = 256.2
(ii) A₂ = 24.44, B₂ = 16.082, C₁ = 240.2
(iii) A₃ = 25.2, B₃ = 19.2812, C₃ = 236.183
(iv) A₄ = 25, B₄ = 236.191, C₄ = 19.5
(a) A₄ + B₄ + C₄ < A₁ + B₁ + C₁ < A₃ + B₃ + C₃ < A₂ + B₂ + C₂
(b) A₁ + B₁ + C₁ = A₂ + B₂ + C₂ = A₃ + B₃ + C₃ = A₄ + B₄ + C₄
(c) A₄ + B₄ + C₄ < A₁ + B₁ + C₁ = A₂ + B₂ + C₂ = A₃ + B₃ + C₃
(d) A₁ + B₁ + C₁ < A₃ + B₃ + C₃ < A₂ + B₂ + C₂ < A₄ + B₄ + C₄

Correct Answer is Option (None)
Solution: 
Given that

So, we have A₁+B₁ +C₁<A₃+B₃+C₃ < A₄+B₄+C₄<A₂+B₂+C₂

Q.60. Expression for time in terms of G (universal gravitational constant), h (Planck constant) and c (speed of light) is proportional to    [(JEE Main 2019)]
(a)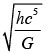
(b)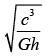
(c)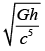
(d)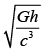

Correct Answer is Option (c)
Solution: 
Dimension of time, t = [T]
Now,
t ∝ G^kh^qc^r
t = kG^kh^qc^r  ....(1)
Dimension of Gravitational constant, G = [M⁻¹L³T⁻²]
Dimension of Planck’s constant h = [ML²T⁻¹]
Dimension of speed of light c = [LT⁻¹]
Put the Dimensions in Eq.(1), we get
[T] = [M^-1L³T^-2]^p[ML²T^-1]^q[LT^-1]^r
[T] = [M^-p+q][L^3p+2q+r][T^-2p-q-r]
On comparing the power of both sides:
-p + q = 0 ⇒ p = q   ....(2)
3p + 2q + r = 0 ⇒ 5p + r = 0    ....(3)
-2p - q - r = 1 ⇒ -3p - r = 1  ....(4)
On solving the above Eq. (2), (3) and (4), we get
p = q = 1/2 and r = -5/2
Put these values in Eq. (1), we get
t = G^1/2h^1/2c^-5/2

where, k = constant

Q.61. The pitch and the number of divisions, on the circular scale, for a given screw gauge are 0.5 mm and 100, respectively. When the screw gauge is fully tightened without any object, the zero of its circular scale lies 3 divisions below the mean line. The readings of the main scale and the circular scale, for a thin sheet, are 5.5 mm and 48 respectively, the thickness of this sheet is    [JEE Main 2019]
(a) 5.755 mm
(b) 5.950 mm
(c) 5.725 mm
(d) 5.740 mm

Correct Answer is Option (c)
Solution: 
Least count = (Pitch/Number of division)
= 0.5/100
= 0.5 × 10^-2 mm
Positive error = 3 × 0.5 × 10⁻² 
= 1.5 × 10⁻²
= 0.015 mm Reading = MSR + CSR – Positive Error
= 5.5 × (48 × 0.5 × 10⁻²) – 0.015
= 5.5 + 0.24 – 0.015
= 5.725 mm

Q.62. The density of a material in SI units is 128 kg/m³. In certain units in which the unit of length is 25 cm and the unit of mass is 50 g, the numerical value of density of the material is     [JEE Main 2019]
(a) 40
(b) 16
(c) 640
(d) 410

Correct Answer is Option (a)
Solution: 
Density = Mass/Voulme
=[M]/[L³]
= [ML^-3]
128 kg/m² = h[50/1000]x[25/100]^-3
= h × (1/20) × (4)³
⇒ h = (128 × 20)/64 = 40 unit

Q.63. The diameter and height of a cylinder are measured by a meter scale to be 12.6 ± 0.1 cm and 34.2 ± 0.1 cm, respectively. What will be the value of its volume in appropriate significant figures?   [JEE Main 2019]
(a) 4264 ± 81 cm³ 
(b) 4264.4 ± 81.0 cm³ 
(c) 4260 ± 80 cm³ 
(d) 4300 ± 80 cm³

Correct Answer is Option (c)
Solution: 
Diameter, D + ΔD = 12.6 ± 0.1 cm
height, h + Δh = 34.2 ± 0.1 cm
Volume of cylinder, V = πr²h
= πd²h/4
= (π/4) × (12.6)² × 34.2
= 4262.229 = 4260
⇒ ΔV/V = 2dD/D + Δh/h
⇒ ΔV = [2 × (0.1/12.6) + (0.1/34.2] × 4266
⇒ ΔV = 80
⇒ V + ΔV = 4260 ± 80 cm³

Q.64. The force of interaction between two atoms is given by F = αβ exp(-x²/αkt), where x is the distance, k is the Boltzmann constant, T is temperature and α and β are two constants. The dimension of β is    (JEE Main 2019)
(a) MLT⁻² 
(b) M²L²T⁻²
(c) M⁰L²T⁻⁴
(d) M²LT⁻⁴

Correct Answer is Option (d)
Solution: 
Given,

⇒ k²/αKT = dimensionless
Dimension of α,
[α] = x²/KT = [L²]/[ML²T^-2]
⇒ [α] = [M^-1T²]
Dimension of F = Dimension of α × Dimension of β
Therefore, dimension of β = (Dimension of F/Dimension of α)
= [MLT^-2]/[M^-1T⁺²]
= [M²LT^-4]

Q.65. If speed (V) , acceleration (A) and force (F) are considered as fundamental units, the dimension of Young’s modulus will be     [JEE Main 2019]
(a) V⁻²A²F⁻²
(b) V⁻²A²F²
(c) V⁻⁴A⁻²F
(d) V⁻⁴A²F

Correct Answer is Option (d)
Solution: 
Young's modulus Y = (F/A x L/L₀)
Dimension of Young’s modulus = [ML⁻¹T⁻²]
Now,
Y ∝ V^a A^b F^c
⇒ Y = KV^aA^bF^c
⇒ [ML^-1T^-2] = [LT^-1]^a[LT^-2]^b [MLT^-2]^c
⇒ [ML^-1T^-2] = [M^c][L^a+b+c][T^-a-2b-2c]
Comparing both the sides, we get
⇒ c = 1
⇒ a + b + c = −1
⇒ −a – 2b – 2c = −2
By solving, we get
a = −4, b = 2, c = 1
Therefore, Y = kV⁻⁴ A²F¹ 
⇒ Y = V⁻⁴A²F

Q.66. The least count of the main scale of a screw gauge is 1 mm. The minimum number of divisions on its circular scale required to measure 5 μm diameter of a wire is     [JEE Main 2019]
(a) 50
(b) 200
(c) 100
(d) 500

Correct Answer is Option (b)
Solution: 
We have,
Least count = 5 μm = 5 × 10⁻⁶ m
Pitch = 1 mm = 10⁻³ m
Thus, least count = (Pitch/Number of divisions on circular scale)
⇒ 5 × 10^-6 = (10^-3/No. of division on circular scale)
Therefore, number of divisions on circular scale = (10^-3/5 × 10^-6)
= 1000/5 = 200

Q.67. Let l, r, c and v represent inductance, resistance, capacitance and voltage, respectively. The dimension of 1/rcv in SI units will be    [JEE Main 2019]
(a) [LA⁻²]
(b) [A⁻¹]
(c) [LTA]
(d) [LT²]

Correct Answer is Option (b)
Solution: 
Dimension of inductance = [M¹L²T⁻²A⁻²] = [l]
Dimension of capacitance = [M⁻¹L⁻²T⁴A²] = [c]
Dimension of resistance = [M¹L²T⁻³A⁻²] = [r]
Dimension of voltage = [M¹L²T⁻³A⁻¹] = [v]
Dimension of l/rcv = [M¹L²T^-2A^-2] / [M^-1L²T⁴A²][M¹L²T^-3A^-2][M¹L²T^-3A^-1]
= [ML²T^-2A^-2]/[ML²T^-2A^-1]
= [A^-1]

Q.68. The density of a material in the shape of a cube is determined by measuring three sides of the cube and its mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum error in determining the density is:    [JEE Main 2018]    
(a) 2.5%
(b) 3.5%
(c) 4.5%
(d) 6%

Correct Answer is Option (c)
Solution: 
p = M/L³
Δp/p = (ΔM/Δ + 3ΔL/L)
= 1.5 + 3 × 1
= 4.5%

Q.69. In a screw gauge, 5 complete rotations of the screw cause it to move a linear distance of 0.25 cm. There are 100 circular scale divisions. The thickness of a wire measured by this screw gauge gives a reading of 4 main scale divisions and 30 circular scale divisions. Assuming negligible zero error, the thickness of the wire is:    [JEE Main 2018]
(a) 0.4300 cm
(b) 0.0430 cm
(c) 0.2150 cm
(d) 0.3150 cm

Correct Answer is Option (c)
Solution: 
Given:  
5 complete rotations of screw = 0.25 cm
So 1 rotation of screw = 0.05
Hence, 1 main scale division = 0.05 cm
and 1 circular scale = 0.05/100 division = 5 × 10⁻⁴ cm.
Now Reading is 4 main scale and 30 circular scale divisions
So , thickness  = 4 × 0.05 + 30 × 5 × 10⁻⁴
= 0.2150 cm.

Q.70. The relative error in the determination of the surface area of a sphere is α. Then the relative error in the determination of its volume is:     [JEE Main 2018]
(a) 5/2 α
(b) 2/3 α
(c) α
(d) 3/2 α

Correct Answer is Option (d)
Solution: 
Area of sphere (A) = 4πR²
Taking log both sides:
ln A = In(4π) + 2In(R)
differentiating both sides
⇒ dA/A = 2dR/R
so, α = 2dR/R
⇒ dR/R = α/2
now, similarly
⇒ dv/v = 3dR/R
So, dv/v = 3α/2

Q.71. The percentage errors in quantities P, Q, R and S are 0.5%, 1%, 3% and 1.5% respectively in the measurement of a physical quantity A = P³Q²/√RS. The maximum percentage error in the value of A will be:    [JEE Main 2018]
(a) 6.5%  
(b) 7.5%
(c) 6.0%
(d) 8.5%

Correct Answer is Option (a)
Solution: 
ΔA/A = 3ΔP/P + 2ΔQ/Q + 1/2(ΔR/R) + ΔS/S
= 3 × 0.5 + 2 × 1 + 1/2 × 3 + 1.5
= 1.5 + 2 + 1.5 + 1.5
ΔA/A = 6.5%

Q.72. The following observations were taken for determining surface tension T of water by capillary method:
Diameter of capillary, D = 1.25 × 10^–2 m
Rise of water, h = 1.45 × 10^–2 m.
Using g = 9.80 m/s² and the simplified relation T= (rhg/2) x 10³ N/m, the possible error in surface tension is closest to     [JEE Main 2017]
(a) 2.4%
(b) 10%
(c) 0.15%
(d) 1.5%

Correct Answer is Option (d)
Solution: 
(ΔT/T) × 100 = (ΔD/D) × 100 + (Δh/h) × 100
= (0.01/1.25) × 100 +(0.01/1.45) × 100
= (100/125) + (100/145)
= 0.8 + 0.689= 1.489
≈ 1.5%

Q.73. Time (T), velocity (3) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be:    [JEE Main 2017]
(a) [M] = [T^–1 C^–2h]
(b) [M] = [T C^–2h]
(c) [M] = [T^–1C^–2h^–1]
(d) [M] = [T^–1 C²h]

Correct Answer is Option (a)
Solution:
M ∝ T^x v^y h^z
M¹ L⁰T⁰ = (T)^x(L¹T^-1)^y(M¹L²T^-1)^z
M¹L⁰T⁰ = M^z L^y+2z + T^x-y-z
z = 1
y + 2z = 0   x - y - z = 0
y = -2          
x + 2 - 1 = 0
x = -1
M ⇒ T^-1 C^-2 h¹

Q.74. A physical quantity P is described by the relation P = a^1/2 b² c³ d^–4 If the relative errors in the measurement of a,b,c and d respectively, are 2%, 1%, 3% and 5%, then the relative error in P will be-    [JEE Main 2017]
(a) 12%
(b) 8%
(c) 25%
(d) 32%

Correct Answer is Option (d)
Solution: 
ΔP/P = (1/2)(Δa/a) + 2(Δb/b) + 3(Δc/c) + 4(Δd/d)
= ((1/2) × 2) + (2 × 1) + (3 × 3) + (4 × 5)
= 32%

Q.75. A student measures the time period of 100 oscillations of a simple pendulum four times. The data set is 90 s, 91 s, 95 s and 92 s. If the minimum division in the measuring clock is 1 s, then the reported mean time should be:    [JEE Main 2016]
(a) 92 ± 2 s
(b) 92 ± 5.0 s
(c) 92 ± 1.8 s
(d) 92 ± 3 s

Correct Answer is Option (a)
Solution: 

 
= (2 + 1 + 3 + 0)/4 = 1.5
L. C. = 1 s.
∴ Required value = 92 ± 2 s

Q.76. A screw gauge with a pitch of 0.5 mm and a circular scale with 50 divisions is used to measure the thickness of a thin sheet of Aluminium. Before starting the measurement, it is found that when the two jaws of the screw gauge and brought in contact, the 45th division coincides with the main scale line and that the zero of the main scale is barely visible. What is the thickness of the sheet if the main scale reading is 0.5 mm and the 25th division coincides with the main scale line?    [JEE Main 2016]
(a) 0.75 mm
(b) 0.80 mm
(c) 0.70 mm
(d) 0.50 mm

Correct Answer is Option (b)
Solution: 
L.C. = (pitch/No. of division on circular scale) = 0.5/50 = 0.001 mm
-ve zero error = - 5 × L.C. = -0.005 mm
∴ Measured value
= main scale reading + screw gauge reading - zero error
= 0.5 mm + {25 × 0.001 - (-0.05)} mm  = 0.80 mm

Q.77. In the following 'I' refers to current and other symbols have their usual meaning choose the option that corresponds to the dimensions of electrical conductivity:    [JEE Main 2016]
(a) M^–1 L^–3 T³ I²
(b) M^–1 L³ T³ I
(c) ML^–3 T^–3 I²
(d) M^–1 L ^–3 T³ I

Correct Answer is Option (a)
Solution: 
J = σE

Q.78. A,B,C and D are four different physical quantities having different dimensions. None of them is dimensionless. But we know that the equation AD = Cln (BD) holds true. Then which of the combination is not a meaningful quantity?    [JEE Main 2016]
(a) A² – B² C²
(b) (A/B) - C
(c) (C/BD) - (AD²/C)
(d) (A-C)/D

Correct Answer is Option (d)
Solution: 
AD = C ln(BD)
(B) (D) → dimensionless
[AD] = [C]
Checking options one by one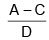
 
Dimensions of A are not same as dimensions of C.