Principal Stress-Strain & Theories of Failure | Strength of Materials (SOM) - Mechanical Engineering PDF Download
What is Principal Stress?
- Principal stress is the maximum or minimum normal stress which may be developed on a loaded body.
- It is classified as major principal stress and minor principal stress.
- On the plane of principal stress, shear stress value is termed as zero.
- When principal stress gets on the major principal plane, it is called major principal stress.
- When it is found on the minor principal plane, it is known as minor principal stress.
- These are denoted as σ1 and σ2, respectively.
Principal Stress Theory
- Shear stress is a sloping applied force that causes deformation due to lateral load.
- In any stress block surface, there is applied shear stress over the plane, but to stabilize the body there, we need to apply complementary shear stress.
- This is known as complementary shear stress.
- The principle of complementary shear stress is when the same intensity but opposite direction shear stress is applied over the surface of the body, it creates a couple and this couple stabilizes the body.
- This balancing couple mechanism is known as the principle of complementary shear stress.
What is Maximum and Minimum Principal Stress?
Principal stress is calculated on the principal plane as maximum stress is called major principal stress, and minimum stress on the principal plane is called minor principal stress.
Here;
- σx = Stress in x direction
- σY = Stress in the Y direction
- τn = Normal shear stress
- Ө = inclination angle of stress to the principal axis
- X and Y are the axes of the plane.
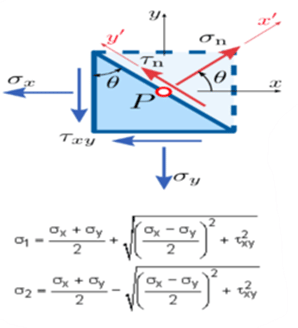
Where
- σ1 is the maximum principal stress, and
- σ2 is the minimum principal stress. it is also termed as σMaxand σMin.
Maximum shear stress (τmax) = (Maximum principal stress- Minor principal stress)/2 =R
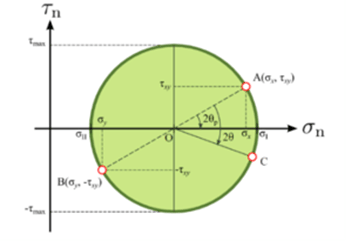
- Here maximum shear stress is the magnitude of that point with an equal radius in a Mohr circle, and the principal stress is the end point of the circle’s diameter.
- Here we take only a two-dimensional theory in which we consider σ1 ( the maximum principal stress ) and σ2 (the minimum principal stress).
- But in the case of three-dimensional theory, we take σ1, σ2, and σ3.
- In this case, we decide on the major or minor principal stress by using principal stress theory or Rankine, Lame’s or maximum principal stress theory.
Maximum Principal Stress Theory
- When the applied load needed to be calculated under the design criteria, the total applied load should be less than the ultimate yield capacity of the material divided by the factor of safety.
- This theory is also a part of principal stress theories, and it's also known as Rankine’s theory, lame’s theory, and reciprocal theory.
- According to the maximum principal stress theory:
- σ1σ2σ3 ≤ yield strength/Factor of safety
Principal Stress and Principal Strain
- Principal stress is related to the existing principal plane available stresses, as when stress is line on the maximum principal planes, as positive and negative stress values of higher magnitudes called principal stress.
- Stress is a tensor because it follows the transformation equation.
- In principal strain, the maximum and minimum normal strains are obtained by differentiating x and y coordinates, and the orientation of the planes of the strains is determined.
- There are two roots, p1 and p2, for 1 and 2 directions.
- Principal strains are the nominal strains with higher magnitude.
What are the Theories of Failure?
- Various load types or combinations act over the components while under operating conditions.
- So, the theories of failure help to give a safe dimension to machine components.
- Before learning about Theories of Failure, let us briefly learn about a machine’s failure.
Failure of Machine
- The meaning of failure of the machine is the non-ability of the component or a machine to perform its function as per requirement.
- Failure of a machine or any mechanical components does not mean a total breakdown or not operating.
- It can operate but not as per our requirements.
The factor of Safety (FOS)
- The ratio of ultimate to allowable load or stress is known as a factor of safety, i.e., the ratio of the material strength or failure stress to the allowable or working stress.
- The factor of safety must always be greater than unity. It is easier to refer to the ratio of stresses since this applies to material properties.
- FOS = Failure Stress/Working or Allowable Stress
Types of Theories of Failure
Based on the loading condition (Tensile load, compressive load, and shear load) and material behavior (Ductile, plastic, and brittle), there are five main theories of failure:
- Maximum principal stress theory or Rankine’s Theory
- Maximum principal strain theory or St. Venant’s Theory
- Maximum Shear Stress Theory or Guest and Tresca’s Theory
- Maximum Strain Energy Theory or Haigh’s Theory
- Maximum Shear Strain Energy theory or Von-Mises and Henckey Theory
Maximum Principal Stress Theory or Rankine’s Theory
In this case of complex loading, when the maximum principal stress value reaches the ultimate stress or yield stress of the material, the component will get failed.
As brittle material is weak in tension, this is most suitable for the brittle material
In simple tension, σ1= σyt
In compression, σ2= σyc
Where,
- σyt– Ultimate tensile stress
- σyc – Ultimate compressive stress
- σ1– Maximum principal stress
Maximum Principal Strain Theory or St. Venant’s Theory
According to this failure theory, components are safe if the maximum principal strain at a critical point in the loaded member will not exceed the strain under the yielding condition when subjected to uniaxial loading. It is the most suitable for all types of material, like ductile material, brittle material, and material under hydrostatic conditions.
It is the most suitable for all types of material, like ductile material, brittle material, and material under hydrostatic conditions.
ε1≤σyt/E
σ1−[ μ ( σ2+ σ3)]≤σyt/E
Where,
- σyt– Ultimate tensile stress
- μ– Poisson ratio
- σ1, σ2, and σ3– Stresses along the x, y, and z-axis
Maximum Shear Stress Theory or Guest and Tresca’s Theory
According to this theory, the material will be failed in the complex loading system at any place in components, and the magnitude of shear stress induced in the material is greater than or equal to the maximum shear stress of the material. Therefore, it is the most suitable theory of failure to experiment on ductile material, especially in the case of a shaft subjected to torque.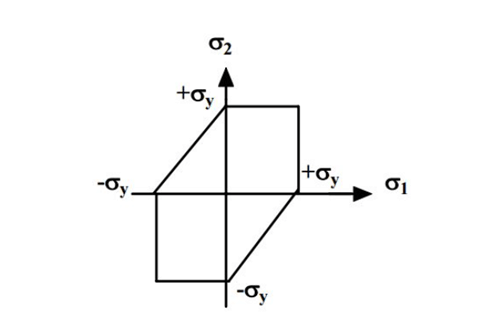
The limitation of maximum shear stress theory is that it will not give proper results for a pure shear loading as well as triaxial tensile or compressive loading having approximately equal magnitude (for example body submerge in water)
Maximum Strain Energy Theory or Haigh’s Theory
Per the maximum strain energy theory, failure occurs when the total strain energy in the fundamental component exceeds strain energy under yield conditions. According to this theory, strain can be fully recoverable up to the elastic limit. However, this theory will not give results in the case of triaxial loading having almost equal magnitude.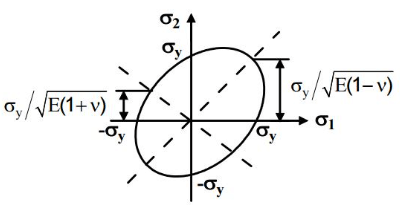
The Strain energy is developed and stored in the material after the elastic deformation. This energy will also be the work done during the elastic transformation. This theory says the developed strain energy will be responsible for the failure of the strain energy under yield conditions.
Maximum Shear Strain Energy Theory or Von-Mises and Henckey Theory
It is also known as the maximum distortion energy theory. As it was introduced by the scientists Von-Mises and Hickey, it is also known as von Mises-Hencky’s theory. When loads are applied to the component, it will deform, due to which the size and shape of the components will change. The energy responsible for changes in shape and volume is known as distortion energy.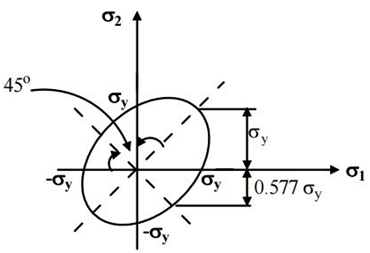 Maximum shear strain theory state that distortion energy associated with the unit volume of the member exceeds the distortion energy at uniaxial loading per unit volume.
Maximum shear strain theory state that distortion energy associated with the unit volume of the member exceeds the distortion energy at uniaxial loading per unit volume.
|
37 videos|106 docs|48 tests
|
FAQs on Principal Stress-Strain & Theories of Failure - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is the significance of principal stress-strain in material behavior? |  |
| 2. How do we calculate the principal stresses from a stress-strain curve? |  |
| 3. What are the theories of failure in material science? |  |
| 4. How does the Maximum Shear Stress Theory determine failure in materials? |  |
| 5. What is the relationship between principal stress-strain and the theories of failure? |  |

















