ICAI Notes- Probability- 2 | Quantitative Aptitude for CA Foundation PDF Download
CONDITIONAL PROBABILITY AND COMPOUND THEOREM OF PROBABILITY
The probability of an event, discussed so far, is technically known as unconditional or marginal probability. However, there are situations that demand the probability of occurrence of more than one event. The probability of occurrence of two events A and B simultaneously is known as the Compound Probability or Joint Probability of the events A and B and is denoted by P(A ∩ B). In a similar manner, the probability of simultaneous occurrence of K events A1, A2,.... Ak, is denoted by P(A1 ∩ A2 ∩ …. ∩ Ak).
In case of compound probability of 2 events A and B, we may face two different situations. In the first case, if the occurrence of one event, say B, is influenced by the occurrence of another event A, then the two events A and B are known as dependent events. We use the notation P(B/A), to be read as 'probability of the event B given that the event A has already occurred (or 'the conditional probability of B given A) to suggest that another event B will happen if and only if the first event A has already happened. This is given by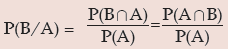
Provided P(A) > 0 i.e. A is not an impossible event.
Similarly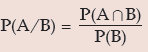
if P(B) > 0.
As an example if a box co ntains 5 red and 8 white balls and two successive draws of 2 balls are made from it without replacement then the probability of the event 'the second draw would result in 2 white balls given that the first draw has resulted in 2 Red balls' is an example of conditional probability since the drawings are made without replacement, the composition of the balls in the box changes and the occurrence of 2 white balls in the second draw (B2) is dependent on the outcome of the first draw (R2). This event may b denoted by P(B2/R2).
In the second scenario, if the occurrence of the second event B is not influenced by the occurrence of the first event A, then B is known to be independent of A. It also follows that in this case, a is also independent of B and A and B are known as mutually independent or just independent.
In this case, we have
P(B/A) = P(B)
and also P(A/B) = P(A)
There by implying, P(A∩ B) = P(A) × P(B)
In the above example, if the balls are drawn with replacement, then the two events B2 and R2 are independent and we have P(B2 / R2) = P(B2) is the necessary and sufficient condition for the independence of two events. In a similar manner, three events A, B and C are known as independent if the following conditions hold: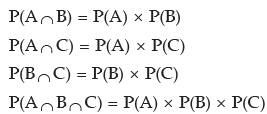
It may be further noted that if two events A and B are independent, then the following pairs of events are also independent: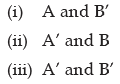
Theorems of Compound Probability
Theorem 5 For any two events A and B, the probability that A and B occur simultaneously is given by the product of the unconditional probability of A and the conditional probability of B given that A has already occurred
i.e. P(A∩ B) = P(A) × P(B/A) Provided P(A) > 0
Theorem 6 For any three events A, B and C, the probability that they occur jointly is given by P(A ∩ B∩ C) = P(A) × P(B/A) × P(C/(A ∩ B)) Provided P(A∩ B) > 0 … (16.32)
In the event of independence of the events
(16.31) and (16.32) are reduced to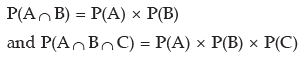
which we have already discussed
Example: Rupesh is known to hit a target in 5 out of 9 shots whereas David is known to hit the same target in 6 out of 11 shots. What is the probability that the target would be hit once they both try?
Solution: Let A denote the event that Rupesh hits the target and B, the event that David hits the target. Then as given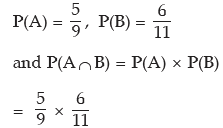
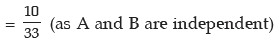
The probability that the target would be hit is given by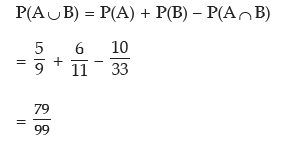
Alternately
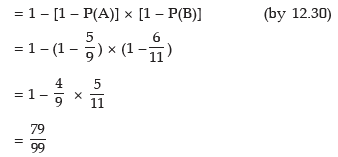
Example: A pair of dice is thrown together and the sum of points of the two dice is noted to be 10. What is the probability that one of the two dice has shown the point 4?
Solution: Let A denote the event of getting 4 points on one of the two dice and B denote the event of getting a total of 10 points on the two dice. Then we have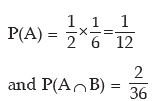
[Since a total of 10 points may result in (4, 6) or (5, 5) or (6, 4) and two of these combinations contain 4]
Alternately The sample space for getting a total of 10 points when two dice are thrown simultaneously is given by S = {(4, 6), (5, 5), (6, 4)}
Out of these 3 cases, we get 4 in 2 cases. Thus by the definition of probability, we have P(B/A) = 2/3
Example: In a group of 20 males and 15 females, 12 males and 8 females are service holders. What is the probability that a person selected at random from the group is a service holder given that the selected person is a male?
Solution: Let S and M stand for service holder and male respectively. We are to evaluate P (S / M). We note that (S ∩M) represents the event of both service holder and male.
Example: In connection with a random experiment, it is found that
Evaluate the following probabilities:
(i) P(A/B) (ii) P(B/A) (iii) P(A’/ B) (iv) P(A/ B’) (v) P(A’/ B’)
Solution: P(A∪ B) = P(A) + P(B) – P(A ∩ B)
Hence (i) P(A/B) = 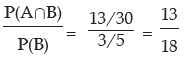
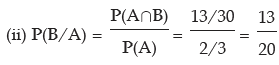
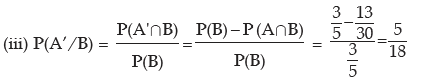
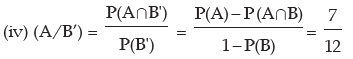
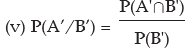

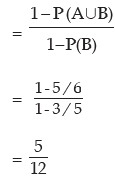
Example: The odds in favour of an event is 2 : 3 and the odds against another event is 3: 7. Find the probability that only one of the two events occurs.
Solution: We denote the two events by A and B respectively. Then by (16.5) and (16.6), we have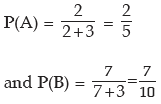
As A and B are independent, P(A∩ B) = P(A) x P(B)
Probability that either only A occurs or only B occurs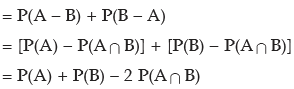
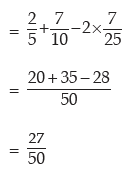
Example: There are three boxes with the following compositions: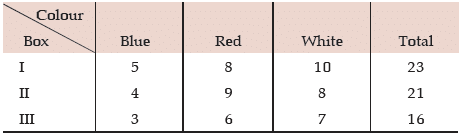
One ball in drawn from each box. What is the probability that they would be of the same colour?
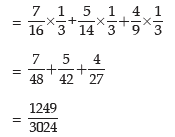
Solution: Either the balls would be Blue or Red or White. Denoting Blue, Red and White balls by B, R and W respectively and the box by lower suffix, the required probability is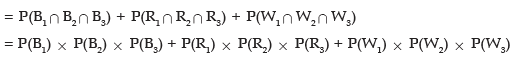
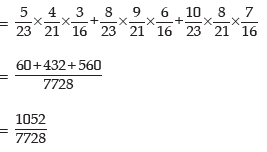
Example: Mr. Roy is selected for three separate posts. For the first post, there are three candidates, for the second, there are five candidates and for the third, there are 10 candidates. What is the probability that Mr. Roy would be selected?
Solution: Denoting the three posts by A, B and C respectively, we have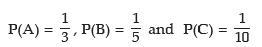
The probability that Mr. Roy would be selected (i.e. selected for at least one post).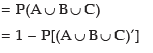
= 1 – P(A’ ∩ B’ ∩ C’) (by De-Morgan's Law)
= 1 – P(A’) x P(B’) x P(C’) (As A , B and C are independent, so are their complements)
Example: The independent probabilities that the three sections of a costing department will encounter a computer error are 0.2, 0.3 and 0.1 per week respectively what is the probability that there would be
(i) at least one computer error per week?
(ii) one and only one computer error per week?
Solution: Denoting the three sections by A, B and C respectively, the probabilities of encountering a computer error by these three sections are given by P(A) = 0.20, P(B) = 0.30 and P(C) = 0.10
(i) Probability that there would be at least one computer error per week.
= 1 – Probability of having no computer error in any at the three sections.
= 1 – P(A’ ∩ B’ ∩ C’)
= 1 – P(A’) x P(B’) x P(C’) [Since A, B and C are independent]
= 1 – (1 – 0.20) x (1 – 0.30) x (1 – 0.10)
= 0.50
(ii) Probability of having one and only one computer error per week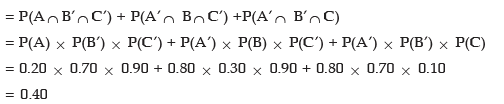
Example: A lot of 10 electronic components is known to include 3 defective parts. If a sample of 4 components is selected at random from the lot, what is the probability that this sample does not contain more than one detectives?
Solution: Denoting detective component and non-defective components by D and D’ respectively, we have the following situation: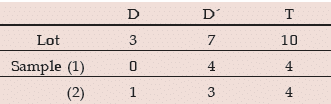
Thus the required probability is given by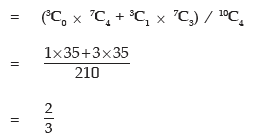
Example: There are two urns containing 5 red and 6 white balls and 3 red and 7 white balls respectively. If two balls are drawn from the first urn without replacement and transferred to the second urn and then a draw of another two balls is made from it, what is the probability that both the balls drawn are red?
Solution: Since two balls are transferred from the first urn containing 5 red and 6 white balls to the second urn containing 3 red and 7 white balls, we are to consider the following cases:
Case A: Both the balls transferred are red. In this case, the second urn contains 5 red and 7 white balls.
Case B: The two balls transferred are of different colours. Then the second urn contains 4 red and 8 white balls.
Case C: Both the balls transferred are white. Now the second urn contains 3 red and 7 white balls. The required probability is given by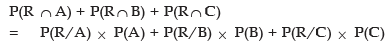
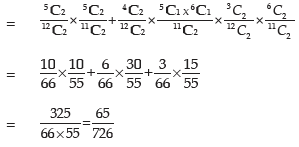
Example: If 8 balls are distributed at random among three boxes, what is the probability that the first box would contain 3 balls?
Solution: The first ball can be distributed to the 1st box or 2nd box or 3rd box i.e. it can be distributed in 3 ways. Similarly, the second ball also can be distributed in 3 ways. Thus the first two balls can be distributed in 32 ways. Proceeding in this way, we find that 8 balls can be distributed to 3 boxes in 38 ways which is the total number of elementary events.
Let A be the event that the first box contains 3 balls which implies that the remaining 5 both must go to the remaining 2 boxes which, as we have already discussed, can be done in 25 ways. Since 3 balls out of 8 balls can be selected in 8C3 ways, the event can occur in 8C3 x 25 ways, thus we have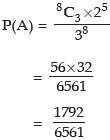
Example: There are 3 boxes with the following composition:
Box I : 7 Red + 5 White + 4 Blue balls
Box II : 5 Red + 6 White + 3 Blue balls
Box III : 4 Red + 3 White + 2 Blue balls
One of the boxes is selected at random and a ball is drawn from it. What is the probability that the drawn ball is red?
Solution: Let A denote the event that the drawn ball is blue. Since any of the 3 boxes may be drawn, we have 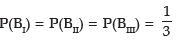
Also P(R1/BII) = probability of drawing a red ball from the first box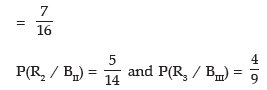
Thus we have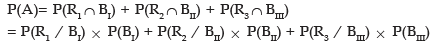
RANDOM VARIABLE - PROBABILITY DISTRIBUTION
A random variable or stochastic variable is a function defined on a sample space associated with a random experiment assuming any value from R and assigning a real number to each and every sample point of the random experiment. A random variable is denoted by a capital letter. For example, if a coin is tossed three times and if X denotes the number of heads, then X is a random variable. In this case, the sample space is given by
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
and we find that X = 0 if the sample point is TTT
X = 1 if the sample point is HTT, THT or TTH
X = 2 if the sample point is HHT, HTH or THH
and X = 3 if the sample point is HHH.
We can make a distinction between a discrete random variable and a continuous variable. A random variable defined on a discrete sample space is known as a discrete random variable and it can assume either only a finite number or a countably infinite number of values. The number of car accident, the number of heads etc. are examples of discrete random variables. A continuous random variable, like height, weight etc. is a random variable defined on a continuous sample space and assuming an uncountably infinite number of values.
The probability distribution of a random variable may be defined as a statement expressing the different values taken by a random variable and the corresponding probabilities. Then if a random variable X assumes n finite values X, X2, X3, …….., Xn with corresponding probabilities
P1, P2, P3, …….., Pn such that
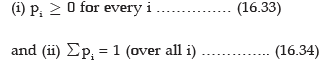
then the probability distribution of the random variable X is given by
For example, if an unbiased coin is tossed three times and if X denotes the number of heads then, as we have already discussed, X is a random variable and its probability distribution is given by
There are cases when it is possible to express the probability (P) as a function of X. In case X is a discrete variable and if such a function f(X) really exists, then f(X) is known as Probability Mass Function (PMF) of X, f(X), then, must satisfy the conditions: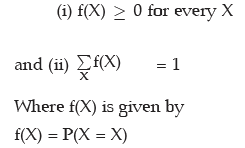
When x is a continuous random variable defined over an interval 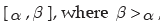 , then x can assume an infinite number of values from its interval and instead of assigning individual probability to every mass point x, we assign probabilities to interval of values. Such a function of x, provided it exists, is known as probability density function (pdf) of x. f(x) satisfies the following conditions:
, then x can assume an infinite number of values from its interval and instead of assigning individual probability to every mass point x, we assign probabilities to interval of values. Such a function of x, provided it exists, is known as probability density function (pdf) of x. f(x) satisfies the following conditions: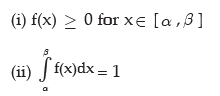
and the probability that x lies between two specified values a and b, where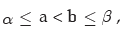 is given by
is given by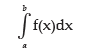
EXPECTED VALUE OF A RANDOM VARIABLE
Expected value or Mathematical Expectation or Expectation of a random variable may be defined as the sum of products of the different values taken by the random variable and the corresponding probabilities. Hence, if a random variable x assumes n values x1, x2, x3 …., xn with corresponding probabilities p1, p2, p3 …., pn , where pi's satisy and (16.34), then the expected value of x is given by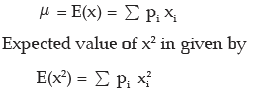
In particular expected value of a monotonic function g (x) is given by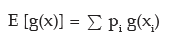
Variance of x, to be denoted by , σ2 is given by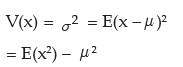
The positive square root of variance is known as standard deviation and is denoted by σ .
If y = a + b x, for two random variables x and y and for a pair of constants a and b, then the mean i.e. expected value of y is given by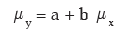
and the standard deviation of y is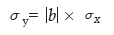
When x is a discrete random variable with probability mass function f(x), then its expected value is given by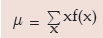
and its variance is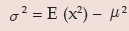
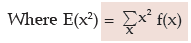
For a continuous random variable x defined in [-∞,∞ ], its expected value (i.e. mean) and variance are given by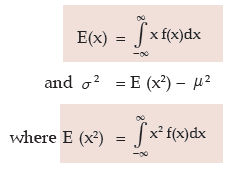
Properties of Expected Values
Expectation of a constant k is k 4. Expectation of the product of two random variables is the product of the expectation of the two random variables, provided the two variables are independent. Whenever x and y are independent. |
Example: An unbiased coin is tossed three times. Find the expected value of the number of heads and also its standard deviation.
Solution: If x denotes the number of heads when an unbiased coin is tossed three times, then the probability distribution of x is given by
The expected value of x is given by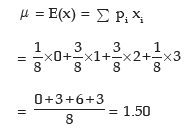
Also,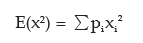

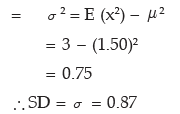
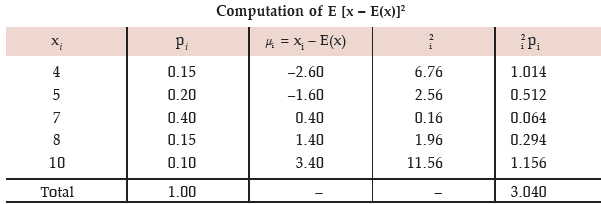
Example: A random variable has the following probability distribution:
Find E [x – E(x)]2. Also obtain v(3x –4)
Solution: The expected value of x is given by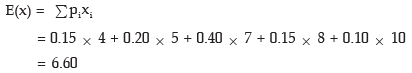
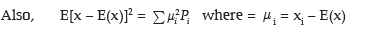
Let y = 3x – 4 = (–4) + (3)x. Then variance of y = var 

Example: In a business venture, a man can make a profit of ₹50,000 or incur a loss of ₹ 20,000. The probabilities of making profit or incurring loss, from the past experience, are known to be 0.75 and 0.25 respectively. What is his expected profit?
Solution: If the profit is denoted by x, then we have the following probability distribution of x:

Example: A box contains 12 electric lamps of which 5 are defectives. A man selects three lamps at random. What is the expected number of defective lamps in his selection?
Solution: Let x denote the number of defective lamps x can assume the values 0, 1, 2 and 3. P(x = 0) = Prob. of having 0 defective out of 5 defectives and 3 non defective out of 7 non defectives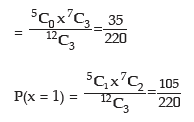

Probability Distribution of No. of Defective Lamp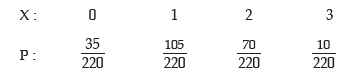
Thus the expected number of defectives is given by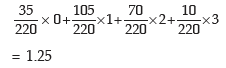
Example: Moidul draws 2 balls from a bag containing 3 white and 5 Red balls. He gets ₹500 if he draws a white ball and ₹200 if he draws a red ball. What is his expectation? If he is asked to pay ₹400 for participating in the game, would he consider it a fair game and participate?
Solution: We denote the amount by x. Then x assumes the value 2 x ₹500 i.e. ₹1000 if 2 white balls are drawn, the value ₹500 + ₹200 i.e. ₹700 if 1 white and 1 red balls are drawn and the value 2 x ₹200 i.e. ₹400 if 2 red balls are drawn. The respective probabilities are given by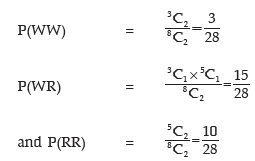
Probability Distribution of x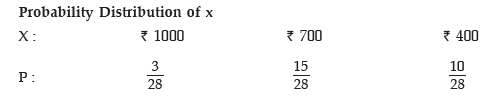
Hence E(x) =

= ₹625 > 400. Therefore the game is fair and he would participate.
Example: A number is selected at random from a set containing the first 100 natural numbers and another number is selected at random from another set containing the first 200 natural numbers. What is the expected value of the product?
Solution: We denote the number selected from the first set by x and the number selected from the second set by y. Since the selections are independent of each other, the expected value of the product is given by
E(xy) = E(x) * E(y)
Now x can assume any value between 1 to 100 with the same probability 1/100 and as such the probability distribution of x is given by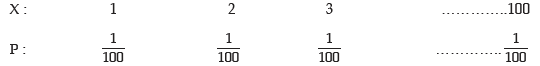
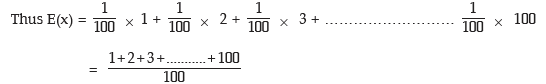
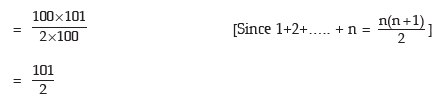
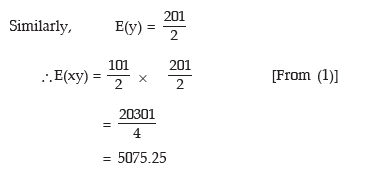
Example: A dice is thrown repeatedly till a 'six' appears. Write down the sample space. Also find the expected number of throws.
Solution: Let p denote the probability of getting a six and q = 1 – p, the probability of not getting a six. If the dice is unbiased then
If a six obtained with the very first throw then the experiment ends and the probability of getting a six, as we have already seen, is p. However, if the first throw does not produce a six, the dice is thrown again and if a six appears with the second throw, the experiment ends. The probability of getting a six preceded by a non–six is qp. If the second thrown does not yield a six, we go for a third throw and if the third throw produces a six, the experiment ends and the probability of getting a Six in the third attempt is q2p. The experiment is carried on and we get the following countably infinite sample space.
S = { p, qp, q2p, q3p, …..}
If x denotes the number of throws necessary to produce a six, then x is a random variable with the following probability distribution: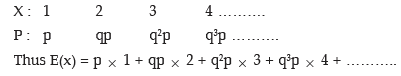
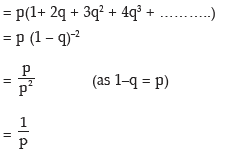
In case of an unbiased dice, p = 1/6 and E(x) = 6
Example: A random variable x has the following probability distribution: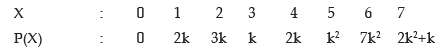
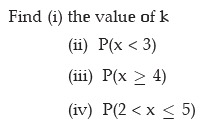
Solution: we have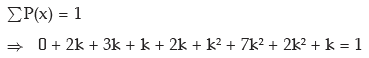
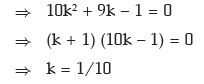 (as k ≠ –1)
(as k ≠ –1)
(i) Thus the value of k is 0.10
(ii) P(x < 3) = P(x = 0) + P(x = 1) + P(x = 2)
= 0 + 2k + 3k
= 5k
= 0.50 (as k = 0.10)
(iii) P(x ≥ 4) = P(x = 4) + P(x = 5) + P(x = 6) + P(x = 7)
= 2k + k2 + 7k2 + (2k2 + k)
= 10k2 + 3k
= 10 x (0.10)2 + 3 x 0.10
= 0.40
(iv) P(2 < x ≤5) = P(x = 3) + P(x = 4) + P(x = 5)
= k + 2k + k2
= k2 + 3k
= (0.10)2 + 3 x 0.10
= 0.31
|
148 videos|174 docs|99 tests
|
FAQs on ICAI Notes- Probability- 2 - Quantitative Aptitude for CA Foundation
| 1. What is probability? |  |
| 2. How is probability calculated? |  |
| 3. What are the different types of probability? |  |
| 4. How are mutually exclusive events related to probability? |  |
| 5. How is conditional probability calculated? |  |
|
148 videos|174 docs|99 tests
|

|
Explore Courses for CA Foundation exam
|

|


















