Probability Distribution of a Random Variable | Mathematics (Maths) for JEE Main & Advanced PDF Download
Probability Distribution
(a) A Probability Distribution spells out how a total probability of 1 is distributed over several values of a random variable.
(b) Mean of any probability distribution of a random variable is given by
(c) Variance of a random variable is given by ⇒
(
SD = +
)
(d) The probability distribution for a binomial variate 'X' is given by ; P (X = r) = nCr pr qn-r. The recurrence formula , is very helpful for quickly computing P(1), P(2), P(3) etc. if P(0) is known.
(e) Mean of BPD = np ; variance of BPD = npq.
(f) If p represents a persons chance of success in any venture and 'M' the sum of money which he will receive in case of success, then his expectations or probable value = pM
expectations = pM
Geometrical Probability
The following statements are axiomatic :
(a) If a point is taken at random on a given straight line AB, the chance that it falls on a particular segment PQ of the line is PQ/AB
(b) If a point is taken at random on the area S which includes an area s, the chance that the points falls on σ is σ/S.
Other Definitions Of Probability
(a) Axiomatic probability : Axiomatic approach is another way of describing probability of an event, in this approach some axioms or rules are depicted to assign probabilities.
Let S be the sample space of a random experiment. The probability P is a real valued function whose domain is the power set of S and range is the interval [0, 1] satisfying the following axioms:
(i) For any event E, P (E) 0
(ii) P(S) = 1
(iii) If E and F are mutually exclusive events, the P (E U F) = P(E) + P(F)
It follows from (iii) that P(φ) = 0

(b) Empirical probability : A method which can be adopted in the example given above is to throw the dart several times (each throw is a trial) and count the number of times you hit the bull's-eye (a success) and the number of times you miss (a failure). Then an empirical value of the probability that you hit the bull's - eye with any one throw is
If the number of throws is small this does not give a particular good estimate but for a large number of throws the result is more reliable.
When the probability of the occurrence of an event A cannot be worked out exactly, an empirical value can be found by adopting the approach described above, that is :
(i) making a large number of trials (i.e. set up an experiment in which the event may, or may not, occur and note the outcome)
(ii) counting the number of times the event does occur, i.e. the number of successes,
(iii) calculating the value of
The probability of then event A occurring is defined as
mean that the number of trials is large (but what should be taken as `large' depends on the problem).
Important Points
(a) If then
and
(b) If where A1, A2, ....... An are mutually exclusive events then P(A) = P(A1) + P(A2) + ...... P(An) = 1
(c) Let A & B are two events corresponding to sample space S then P(S|A) = P(A|A) = 1
(d) Let A and B are two events corresponding to sample space S and F is any other event s.t. P(F) ≠ 0 then
(e)
(f)
Ex 1. A, B, C in order cut a pack of cards, replacing them after each cut, on the condition that the first who cuts a spade shall win a prize; find their respective chances.
Sol. Let p be the chance of cutting a spade and q be the chance of not cutting a spade from a pack of 52 cards. Then and
Now A will win a prize if he cuts spade at 1st, 4th, 7th, 10th turns, etc. Note that A will get a second chance if A, B, C all fail to cut a spade once and then A cuts a spade at the 4th turn.
Similarly he will cut a spade at the 7th turn when A, B, C fail to cut spade twice, etc.
Hence A's chance of winning the prize =
Similarly B's chance
and C's chance of B's chance
Ex.2 (a) If p and q are chosen randomly from the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, with replacement, determine the probability that the roots of the equation x2 + px + q = 0 are real.
(b) Each coefficient in the equation ax2 + bx + c = 0 is determined by throwing at ordinary die. Find the probability that the equation will have equal roots.
Sol. (a) If roots of x2 + px + q = 0 are real, then p2 - 4q 0 ....(i)
Both p, q belongs to set when p = 1, no value of q from S will satisfy (i)
p = 2 ,q = 1 will satisfy, 1 value
p = 3 ,q = 1, 2 ,2 value
p = 4 , q = 1, 2, 3, 4 ,4 value
p = 5 , q = 1, 2, 3, 4, 5, 6, 6 value
p = 6 ,q = 1, 2, 3, 4, 5, 6, 7, 8, 9, ,9 value
For p = 7, 8, 9, 10 all the ten values of q will satisfy.
Sum of these selections in 1 + 2 + 4 + 6 + 9 + 10 + 10 + 10 = 62
But the total number of selections of p and q without any order is 10 × 10 = 100
Hence the required probability is
(b) Roots equal
....(i)
Each coefficient is an integer, so we consider the following cases :
b = 1 , No integral values of a and c
b = 2 , 1 = ac 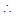 (1, 1)
(1, 1)
b = 3 , 9/2 = ac No integral values of a and c
b = 4 , 4 = ac 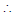 (1, 4), (2, 2), (4, 1)
(1, 4), (2, 2), (4, 1)
b = 5 , 25/2 = ac No integral values of a and c
b = 6 ,9 = ac 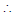 (3, 3)
(3, 3)
Thus we have 5 favourable way for b = 2, 4, 6,
Total number of equations is 6.6.6 = 216 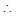 Required probability is
Required probability is
Ex.3 In a test an examinee either guesses or copies or knows the answer to a multiple choice question with four choices. The probability that he makes a guess is and the probability that he copies the answer is . The probability that his answer is correct given that he copied it, is
. Find the probability that he knew the answer to the question given that he correctly answered it.
Sol. Let A1 be the event that the examinee guesses that answer ; A2 the event that he copies the answer and A3 the event that he knows the answer. Also let A be the event that he answers correctly. Then as given, we have
[We have assumed here that the events A1, A2 and A3 are mutually exclusive and totally exhaustive.]
Now (as given)
Again it is reasonable to take the probability of answering correctly given that he knows the answer as 1, that is . We have to find
.
By Baye's theorem, we have
Ex.4 A lot contains 50 defective and 50 non-defective bulbs. Two bulbs are drawn at random, one at a time, with replacement. The events A, B, C are defined as
A = {The first bulb is defective}
B = {The second bulb is non-defective}
C = {The two bulbs are both defective or both non-defective}
Determine whether
(i) A, B, C are pairwise independent,
(ii) A, B, C are independent.
Sol. We have ;
;
is the event that first bulb is defective and second is non-defective.
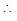
is the event that first bulb is defective and second is non-defective.
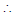
Similarly . Thus we have
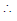 A, B and C are pairwise independent. There is no element in
A, B and C are pairwise independent. There is no element in
Hence A, B and C are not mutually independent.
|
172 videos|503 docs|154 tests
|
FAQs on Probability Distribution of a Random Variable - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a probability distribution of a random variable? |  |
| 2. How is a probability distribution different from a probability density function (PDF)? |  |
| 3. What are the types of probability distributions commonly used in statistics? |  |
| 4. How can probability distributions be used in real-life applications? |  |
| 5. What is the expected value of a random variable and how is it calculated? |  |
















