Important Formulas: Probability | CSAT Preparation - UPSC PDF Download
What is Probability?
Probability can be seen as a predictive measure, denoted by the variable "x," representing the likelihood of an event happening, while (1-x) corresponds to the chances of the event not occurring. The probability formula serves to calculate the likelihood of an event taking place in a random experiment.
Probability or Chance: Probability or chance is a common term used in day-to-day life.
Example: We generally say, 'It may rain today'. This statement has a certain uncertainty.
Probability is a quantitative measure of the chance of occurrence of a particular event.
Experiment: An experiment is an operation which can produce well-defined outcomes.
Random Experiment: If all the possible outcomes of an experiment are known but the exact output cannot be predicted in advance, that experiment is called a random experiment.

Examples:
Tossing of a fair coin: When we toss a coin, the outcome will be either Head (H) or Tail (T).
Throwing an unbiased die: Die is a small cube used in games. It has six faces and each of the six faces shows a different number of dots from 1 to 6. Plural of die is dice.
When a die is thrown or rolled, the outcome is the number that appears on its upper face and it is a random integer from one to six, each value being equally likely.
Drawing a card from a pack of shuffled cards: A pack or deck of playing cards has 52 cards which are divided into four categories as given below. Each of the above-mentioned categories has 13 cards, 9 cards numbered from 2 to 10, an Ace, a King, a Queen and a Jack of Hearts and Diamonds are red-faced cards whereas Spades and Clubs are black-faced cards.
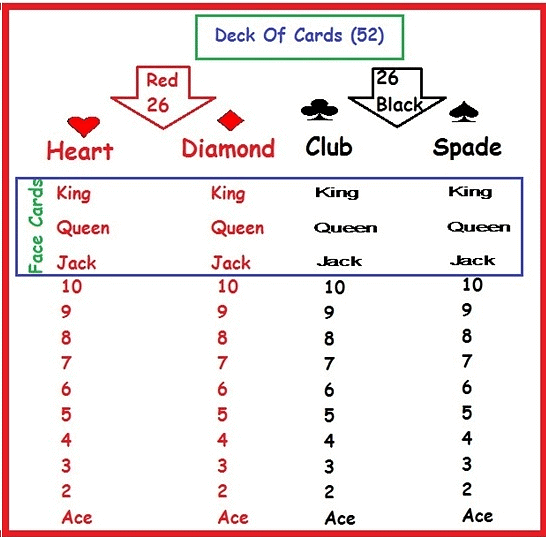
Kings, Queens and Jacks are called face cards:
(i) Spades (♠)
(ii) Clubs (♣)
(iii) Hearts (♥)
(iv) Diamonds (♦)Taking a ball randomly from a bag containing balls of different colours.
Question for Important Formulas: ProbabilityTry yourself:A bag has 5 white marbles, 8 red marbles and 4 purple marbles. If we take a marble randomly, then what is the probability of not getting purple marble?View Solution
Sample Space: Sample Space is the set of all possible outcomes of an experiment. It is denoted by S.
Examples:
(i) When a coin is tossed, S = {H, T} where H = Head and T = Tail
(ii) When a dice is thrown, S = {1, 2 , 3, 4, 5, 6}
(iii) When two coins are tossed, S = {HH, HT, TH, TT} where H = Head and T = Tail
Event: Any subset of a Sample Space is an event. Events are generally denoted by capital letters A, B , C, D etc.
Examples:
(i) When a coin is tossed, outcome of getting head or tail is an event
(ii) When a die is rolled, outcome of getting 1 or 2 or 3 or 4 or 5 or 6 is an event.
Probability of an Event
Let E be an event and S be the sample space. Then probability of the event E can be defined as:where P(E) = Probability of the event E, n(E) = number of ways in which the event can occur and n(S) = Total number of outcomes possibleP(S) = 1
0 ≤ P (E) ≤ 1
P(ϕ) = 0 (∵ Probability of occurrence of an impossible event = 0)
Examples:
(i) A coin is tossed once. What is the probability of getting Head?
Total number of outcomes possible when a coin is tossed = n(S) = 2 (∵ Head or Tail)
E = event of getting Head = {H}. Hence n(E) = 1
(ii) Two dice are rolled. What is the probability that the sum on the top face of both the dice will be greater than 9?
Total number of outcomes possible when a die is rolled = 6 (∵ any one face out of the 6 faces)
Hence, total number of outcomes possible two dice are rolled, n(S) = 6 × 6 = 36
E = Getting a sum greater than 9 when the two dice are rolled = {(4, 6), {5, 5}, {5, 6}, {6, 4}, {6, 5}, (6, 6)}
Hence, n(E) = 6.
Types of Events
Equally Likely Events: Events are said to be equally likely if there is no preference for a particular event over the other.
Examples:
(i) When a coin is tossed, Head (H) or Tail is equally likely to occur.
(ii) When a dice is thrown, all the six faces (1, 2, 3, 4, 5, 6) are equally likely to occur.
Mutually Exclusive Events: Two or more than two events are said to be mutually exclusive if the occurrence of one of the events excludes the occurrence of the other.
This can be better illustrated with the following examples:
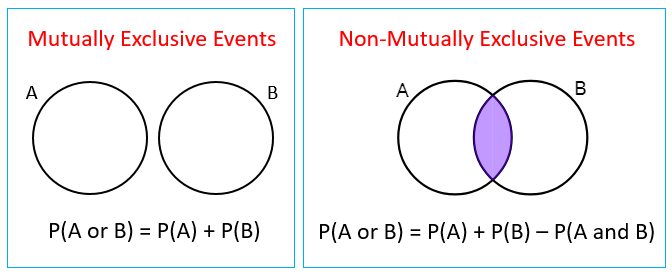
Note: If A and B are mutually exclusive events, A ∩ B = ϕ where ϕ represents empty set.
(i) When a coin is tossed, we get either Head or Tail. Head and Tail cannot come simultaneously. Hence occurrence of Head and Tail are mutually exclusive events.
(ii) When a die is rolled, we get 1 or 2 or 3 or 4 or 5 or 6. All these faces cannot come simultaneously. Hence occurrences of particular faces when rolling a die are mutually exclusive events.
(iii) Consider a die is thrown and A be the event of getting 2 or 4 or 6 and B be the event of getting 4 or 5 or 6. Then A = {2, 4, 6} and B = {4, 5, 6}
Here A ∩ B ≠ ϕ. Hence A and B are not mutually exclusive events.Question for Important Formulas: ProbabilityTry yourself:If we throw two coins in the air, then the probability of getting both tails will be:View SolutionIndependent Events: Events can be said to be independent if the occurrence or non-occurrence of one event does not influence the occurrence or non-occurrence of the other.

Example: When a coin is tossed twice, the event of getting Tail(T) in the first toss and the event of getting Tail(T) in the second toss are independent events. This is because the occurrence of getting Tail(T) in any toss does not influence the occurrence of getting Tail(T) in the other toss.
Simple Events: In the case of simple events, we take the probability of occurrence of single events.
Examples:
(i) Probability of getting a Head (H) when a coin is tossed.
(ii) Probability of getting 1 when a die is thrown.Compound Events: In the case of compound events, we take the probability of joint occurrence of two or more events.
Example: When two coins are tossed, probability of getting a Head (H) in the first toss and getting a Tail (T) in the second toss.
Exhaustive Events: Exhaustive Event is the total number of all possible outcomes of an experiment.
Examples:
(i) When a coin is tossed, we get either Head or Tail. Hence there are 2 exhaustive events.
(ii) When two coins are tossed, the possible outcomes are (H, H), (H, T), (T, H), (T, T). Hence there are 4 (=22) exhaustive events.
(iii) When a dice is thrown, we get 1 or 2 or 3 or 4 or 5 or 6. Hence there are 6 exhaustive events.
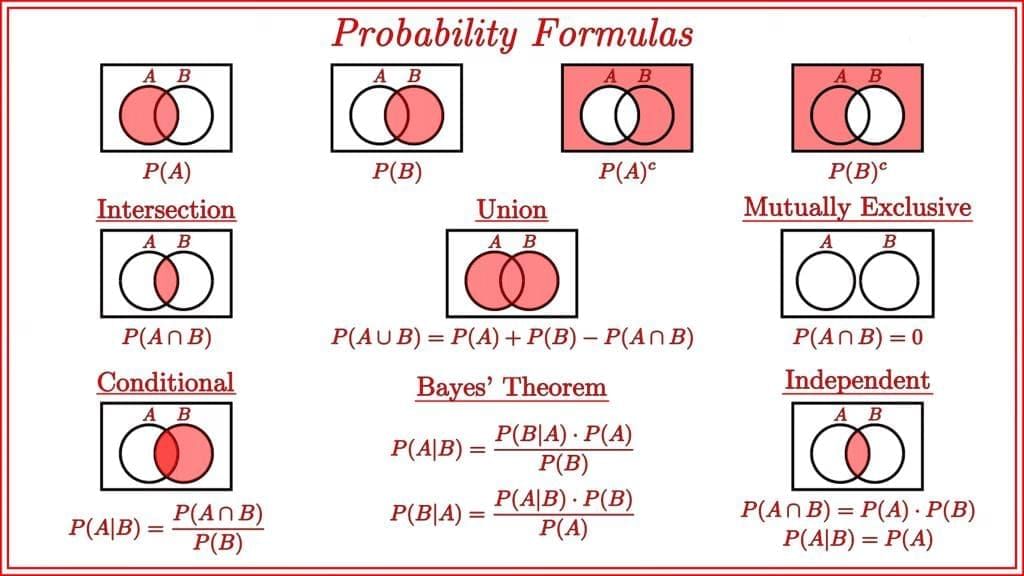
Unions ,Intersections and Complements
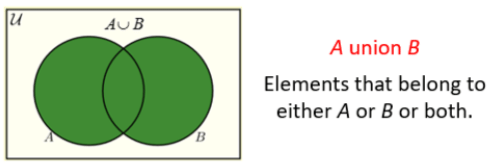
- The union of two sets contains all the elements contained in either set (or both sets). The union is notated A ⋃ B.
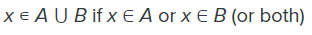
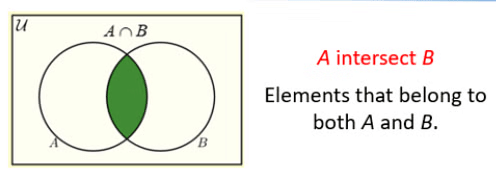
- The intersection of two sets contains only the elements that are in both sets. The intersection is notated A ⋂ B.
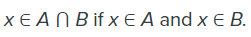
- The complement of a set A contains everything that is not in the set A.
The complement is notated as follows
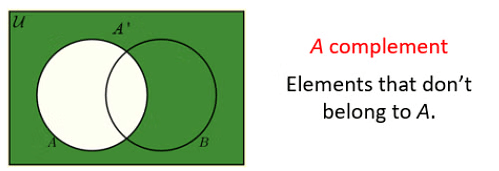
Following image shows Venn Diagrams of the above terms.
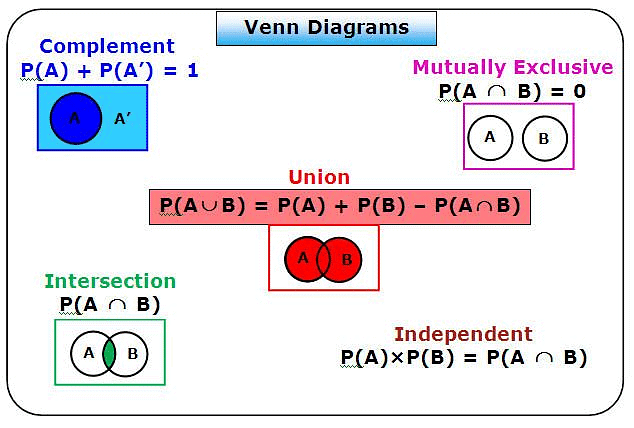 Venn Diagrams and Formulae
Venn Diagrams and Formulae
Algebra of Events
Let A and B are two events with sample space S. ThenOther Important Calculations
- Addition Theorem:
Let A and B be two events associated with a random experiment. Then
P(A U B) = P(A) + P(B) – P(A ∩ B)
If A and B are mutually exclusive events, then P(A U B) = P(A) + P(B) because for mutually exclusive events, P(A ∩ B) = 0.
Independent Events:
If A and B are two independents events, thenP(A ∩ B) = P(A).P(B)
Example: Two dice are rolled. What is the probability of getting an odd number in one die and getting an even number in the other die?
Total number of outcomes possible when a die is rolled, n(S) = 6 (∵ any one face out of the 6 faces)
Let A be the event of getting the odd number in one die = {1,3,5}. => n(A)= 3
Let B be the event of getting an even number in the other die = {2,4, 6}. => n(B)= 3
Required Probability, P(A ∩ B) = P(A).P(B) =
Let A be any event and A¯ be its complementary event (i.e., A¯ is the event that A does not occur). Then
Odds on an Event
Let E be an event associated with a random experiment. Let x outcomes are favourable to E and y outcomes are not favourable to E, then
Example:
What are the odds in favour of and against getting a 1 when a die is rolled?Let E be an event of getting 1 when a die is rolled
Outcomes which are favourable to E, x=1
Outcomes which are not favourable to E, y=5
Conditional Probability
Let A and B be two events associated with a random experiment. Then, probability of the occurrence of A given that B has already occurred is called conditional probability and denoted by P(A/B).
Example: A bag contains 5 black and 4 blue balls. Two balls are drawn from the bag one by one without replacement. What is the probability of drawing a blue ball in the second draw if a black ball is already drawn in the first draw?
Solution: Let A be the event of drawing black ball in the first draw and B be the event of drawing a blue ball in the second draw. Then, P(B/A) = Probability of drawing a blue ball in the second draw given that a black ball is already drawn in the first draw.
Total Balls = 5 + 4 = 9
Since a black ball is drawn already,
total number of balls left after the first draw = 8
total number of blue balls after the first draw = 4
Binomial Probability Distribution
A binomial experiment is a probability experiment which satisfies the following requirements:
(i) Each trial can have only two outcomes. These outcomes can be considered as either success or failure.
(ii) There must be a fixed number of trials.
(iii) The outcomes of each trial must be independent of each other.
(iv) The probability of a success must remain the same for each trial.
In a binomial experiment, The probability of achieving exactly r successes in n trials can be given by:
where p = probability of success in one trial, q = 1 - p = probability of failure in one trial

Note: If n fair coins are tossed, Total number of outcomes in the sample space = 2n
The probability of getting exactly r-number of heads when n coins are tossed =
|
205 videos|264 docs|136 tests
|
FAQs on Important Formulas: Probability - CSAT Preparation - UPSC
| 1. What is the formula for calculating the probability of an event? |  |
| 2. What are the types of events in probability theory? |  |
| 3. How do you calculate the conditional probability of an event? |  |
| 4. What is the algebra of events in probability theory? |  |
| 5. How is the binomial probability distribution used in probability calculations? |  |

















