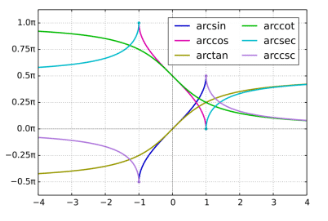
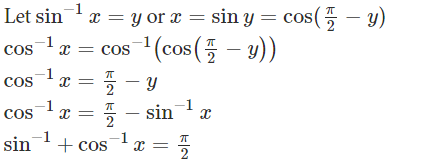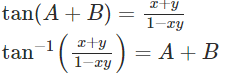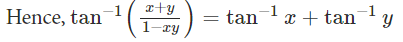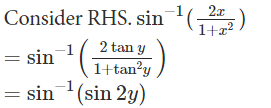The inverse trigonometric functions are also called arcus functions or anti trigonometric functions. These are the inverse functions of the trigonometric functions with suitably restricted domains. Specifically, they are the inverse functions of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle’s trigonometric ratios.
Properties of Trigonometric Inverse Functions
Here are the properties of the inverse trigonometric functions with proof.
Property 1
i. sin-1 (1/x) = cosec-1x , x ≥ 1 or x ≤ -1
ii. cos-1 (1/x) = sec-1x , x ≥ 1 or x ≤ -1
iii. tan-1 (1/x) = cot-1x , x > 0
Proof : sin-1 (1/x) = cosec-1x , x ≥ 1 or x ≤ -1,
Let sin−1 x = y
i.e. x = cosec y
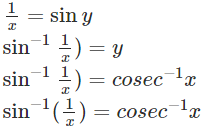
Hence, 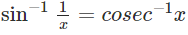 where, x ≥ 1 or x ≤ -1.
where, x ≥ 1 or x ≤ -1.
Property 2
i. sin-1(-x) = – sin-1(x), x ∈ [-1,1]
ii. tan-1(-x) = -tan-1(x), x ∈ R
iii. cosec-1(-x) = -cosec-1(x), |x| ≥ 1
Proof: sin-1(-x) = -sin-1(x), x ∈ [-1,1]
Let, sin−1(−x) = y
Then −x = sin y
x = −sin y
x = sin(−y)
sin−1 = sin−1(sin(−y))
sin−1 x = y
sin−1 x = −sin−1(−x)
Hence,sin−1(−x)=−sin−1 x ∈ [-1,1]
Property 3
i. cos-1(-x) = π – cos-1 x, x ∈ [-1,1]
ii. sec-1(-x) = π – sec-1x, |x| ≥ 1
iii. cot-1(-x) = π – cot-1x, x ∈ R
Proof : cos-1(-x) = π – cos-1 x, x ∈ [-1,1]
Let cos−1(−x) = y
cos y = −x x = −cos y
x = cos(π−y)
Since, cosπ − q = −cos q
cos−1x = π − y
cos−1x = π–cos−1–x
Hence, cos−1−x = π–cos−1x
Property 4
i. sin-1x + cos-1x = π/2, x ∈ [-1,1]
ii. tan-1x + cot-1x = π/2, x ∈ R
iii. cosec-1x + sec-1x = π/2, |x| ≥ 1
Proof : sin-1x + cos-1x = π/2, x ∈ [-1,1]
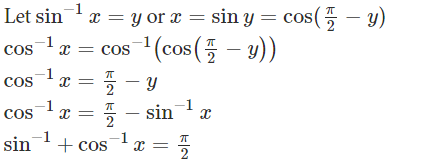
Hence, sin-1x + cos-1x = π/2, x ∈ [-1,1]
Property 5
tan-1x + tan-1y = tan-1((x+y)/(1-xy)), xy < 1.
tan-1x – tan-1y = tan-1((x-y)/(1+xy)), xy > -1.
Proof : tan-1x + tan-1y = tan-1((x+y)/(1-xy)), xy < 1.
Let tan−1x = A
And tan−1y = B
Then, tan A = x
tan B = y
Now, tan(A+B)=(tanA+tanB)/(1−tanAtanB)
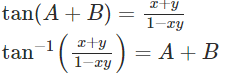
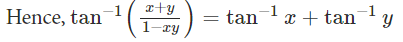
Property 6
i. 2tan-1x = sin-1 (2x/(1+x2)), |x| ≤ 1
ii. 2tan-1x = cos-1((1-x2)/(1+x2)), x ≥ 0
iii. 2tan-1x = tan-1(2x/(1 – x2)), -1 < x <1
Proof : 2tan-1x = sin-1 (2x/(1+x2)), |x| ≤ 1
Let tan−1x = y and x = tan y
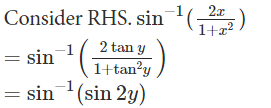
Since, sin2θ = 2tanθ/(1+tan2θ),
= 2y
= 2tan−1x which is our LHS
Hence 2 tan-1x = sin-1 (2x/(1+x2)), |x| ≤ 1
Solved Example
Q1. Prove that “sin-1(-x) = – sin-1(x), x ∈ [-1,1]”
Ans: Let, sin−1(−x) = y
Then −x = siny
x = −siny
x = sin(−y)
sin−1x = arcsin(sin(−y))
sin−1x = y
sin−1x = −sin−1(−x)
Hence, sin−1(−x)=−sin−1x, x ∈ [-1,1]

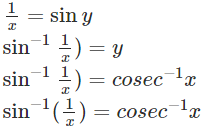
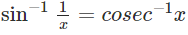 where, x ≥ 1 or x ≤ -1.
where, x ≥ 1 or x ≤ -1.