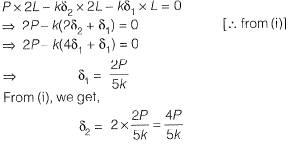Past Year Questions: Properties of Metals, Stress & Strain | Civil Engineering SSC JE (Technical) - Civil Engineering (CE) PDF Download
Q1: A homogeneous, prismatic, linearly elastic steel bar fixed at both the ends has a slenderness ratio (I/r) of 105, where I is the bar length and r is the radius of gyration. The coefficient of thermal expansion of steel is 12 × 10−6/∘C. Consider the effective length of the steel bar as 0.51 and neglect the self-weight of the bar. The differential increase in temperature (rounded off to the nearest integer) at which the bar buckles is [2024, Set-I]
(a) 250°C
(b) 400°C
(c) 85°C
(d) 298°C
Ans: (d)
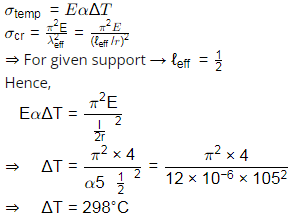
Q2: Consider the fillet-welded lap joint shown in the figure (Not to scale). The length of the weld shown in the effective length. The welded surface meet at right angle. The weld size is 8 mm, and the permissible stress in the weld is 120MPa. What is the safe load P (in kN, rounded off to one decimal place) that can be transmitted by this welded joint ? [2023, Set-I]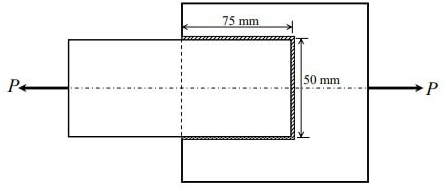 (a) 185.2
(a) 185.2
(b) 111.3
(c) 214.5
(d) 134.3
Ans: (d)
Given data,
Weld size = 8 mm
Permissible stress =120MPa
Effective throat thickness, te = 0.7 × Weld size = 0.7 × 8 = 5.6 m
Total effective length of weld, ℓe = 2 × 75 + 50 = 200m
⇒ Safe load 'P' in kN rounded upto one decimal palce
= 5.6 × 200 × 120 × 10−3
= 134.4 k N
Q3: Consider two linearly elastic rods HI and IJ, each of length b, as shown in the figure. The rods are co-linear, and confined between two fixed supports at H and J. Both the rods are initially stress free. The coefficient of linear thermal expansion is α for both the rods. The temperature of the rod IJ is raised by ΔT, whereas the temperature of rod HI remains unchanged. An external horizontal force P is now applied at node I. It is given that α = 10−6ºC−1 ,ΔT = 50º C-1, b = 2m, AE = 106 N. The axial rigidities of the rods HI and IJ are 2AE and AE, respectively. [2022, Set-II] 
To make the axial force in rod HI equal to zero, the value of the external force P (in N) is _________. (round off to the nearest integer)
(a) 85
(b) 23
(c) 65
(d) 50
Ans: (d)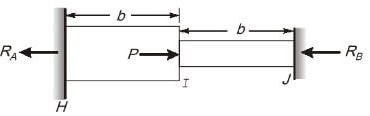
RA + RB = P
∵ There is no axial force in rod HI
∴ RA= 0
Now check for rod IJ Now as rod IJ is fixed from both end, so net deflection due to increase in temperature will be zero.
Now as rod IJ is fixed from both end, so net deflection due to increase in temperature will be zero.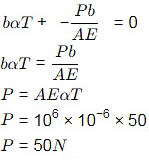
Q4: For a linear elastic and isotropic material, the correct relationship among Young's modulus of elasticity (E), Poisson's ratio (v), and shear modulus (G) is [2022, Set-II]
(a)
(b)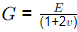
(c)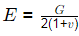
(d)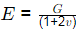
Ans: (a)
E = 2G(1+μ)
G = Shear modulas
μ = Poission's ratio
E = Young's modulus
Q5: Strain hardening of structural steel means [2021, Set-II]
(a) experiencing higher stress than yield stress with increased deformation
(b) strengthening steel member externally for reducing strain experienced
(c) strain occurring before plastic flow of steel material
(d) decrease in the stress experienced with increasing strain
Ans: (a)
Strain hardening is experiencing higher stress than yield stress with increased deformation
In the figure AB = Strain hardening zone
OA = Linear elastic zone
Stress corresponding to point 'A' is yield stress.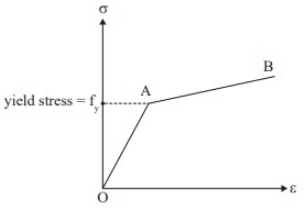
Q6: A square plate O-P-Q-R of a linear elastic material with sides 1.0 m is loaded in a state of plane stress. Under a given stress condition, the plate deforms to a new configuration O-P'-Q'-R' as shown in the figure (not to scale). Under the given deformation, the edges of the plate remain straight. [2021, Set-I]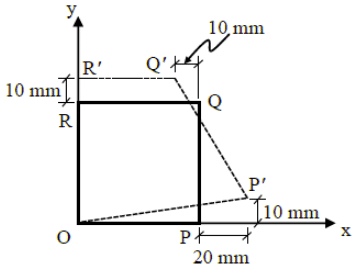 The horizontal displacement of the point (0.5 m, 0.5 m) in the plate O-P-Q-R (in mm,round off to one decimal place) is ________
The horizontal displacement of the point (0.5 m, 0.5 m) in the plate O-P-Q-R (in mm,round off to one decimal place) is ________
(a) 1.2
(b) 6.3
(c) 5.2
(d) 2.5
Ans: (d)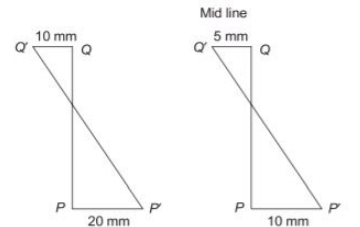 So horizontal displacement of the point (0.5 m, 0.5 m)
So horizontal displacement of the point (0.5 m, 0.5 m)
= − 2.5 mm + 5 mm = 2.5 m
Q7: The state of stress represented by Mohr's circle shown in the figure is [2020, Set-II]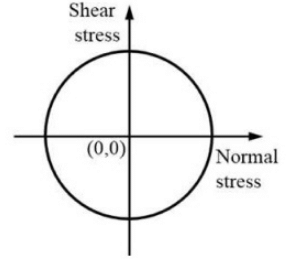 (a) uniaxial tension
(a) uniaxial tension
(b) biaxial tension of equal magnitude
(c) hydrostatic stress
(d) pure shear
Ans: (d)
In pure shear condition, Mohr's circle has its center at origin.
Q8: A rigid, uniform, weightless, horizontal bar is connected to three vertical members P, Q and R as shown in the figure. All three members have identical axial stiffness of 10 kN/mm. The lower ends of bars P and R rest on a rigid horizontal surface. When NO laod is applied, a gap of 2 mm exist between the lower end of the bar Q and the rigid horizontal surface. When a vertical load W is placed on the horizontal bar in the downward direction, the bar still remains horizontal and gets displayed by 5 mm in the vertically downward direction. [2020, Set-I]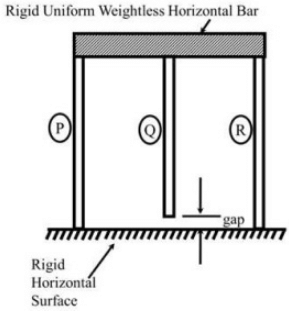 The magnitude of the load W (in kN, round off to the nearst integer), is ______
The magnitude of the load W (in kN, round off to the nearst integer), is ______
(a) 110
(b) 150
(c) 130
(d) 160
Ans: (c)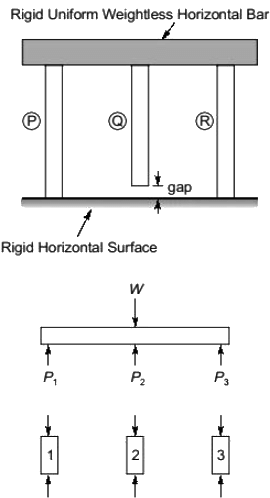 P1 + P1 + P2 = W
P1 + P1 + P2 = W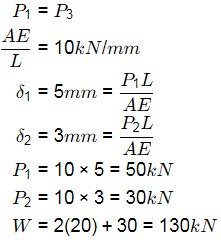
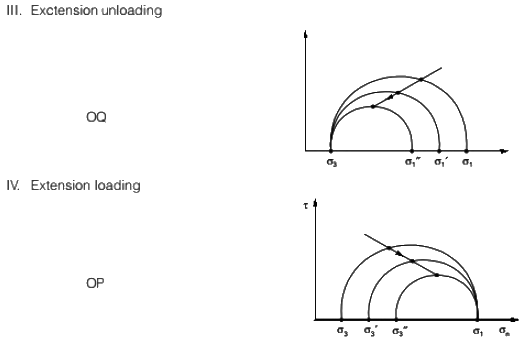
Q9: The total stress paths corresponding to different loading conditions, for a soil specimen under the isotropically consolidated stress state (O), are shown below: [2020, Set-I]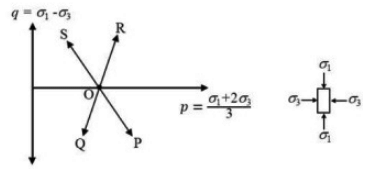
 The correct match between the stress paths and the listed loading conditions, is
The correct match between the stress paths and the listed loading conditions, is
(a) OP-I, OQ-II, OR-IV, OS-III
(b) OP-IV, OQ-III, OR-I, OS-II
(c) OP-III, OQ-II, OR-I, OS-IV
(d) OP-I, OQ-III, OR-II, OS-IV
Ans: (b)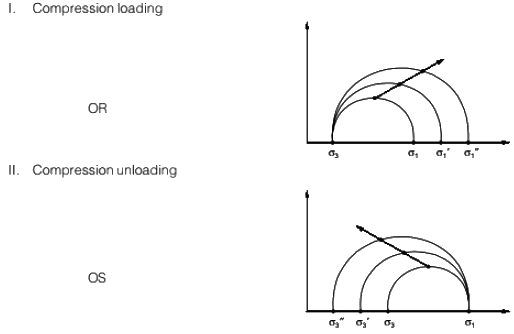
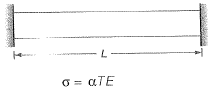
Q10: An isolated concrete pavement slab of length L is resting on a frictionless base. The temperature of the top and bottom fibre of the slab are Tt and Tb , respectively. Given: the coefficient of thermal expansion = α and the elastic modulus = E. Assuming Tt > Tb and the unit weight of concrete as zero, the maximum thermal stress is calculated as [2019, Set-I]
(a) Lα(Tt - Tb)
(b) Eα(Tt - Tb)
(c)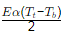
(d) Zero
Ans: (d)
Due to frictionless, thermal stress developed in concrete pavement slab is zero σth= 0
Q11: An element is subjected to biaxial normal tensile strains of 0.0030 and 0.0020. The normal strain in the plane of maximum shear strain is [2019, Set-I]
(a) Zero
(b) 0.001
(c) 0.0025
(d) 0.005
Ans: (c)
εx = 0.0030
εy = 0.0020
Normal strain in the plane of maximum shear strain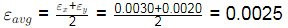
Q12: A plate in equilibrium is subjected to uniform stresses along its edges with magnitude σxx = 30 MPa and σyy = 50 MPa as shown in the figure. The Young’s modulus of the material is 2 x 1011 N/m2 and the Poisson’s ratio is 0.3. If σzz is negligibly small and assumed to be zero, then the strain εzz is _________. [2018 : 2 Marks, Set-I]
The Young’s modulus of the material is 2 x 1011 N/m2 and the Poisson’s ratio is 0.3. If σzz is negligibly small and assumed to be zero, then the strain εzz is _________. [2018 : 2 Marks, Set-I]
(a) -120 x 10-6
(b) -60 x 10-6
(c) 0.0
(d) 120 x 10-6
Ans:
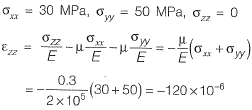 So the answer is (d).
So the answer is (d).
Q13: A 2 m long, axially loaded mild steel rod of 8 mm diameter exhibits the load-displacement (P-δ) behaviour as shown in the figure.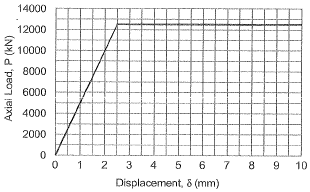 Assume the yield stress of steel as 250 MPa. The complementary strain energy (in N-mm) stored in the bar up to its linear elastic behaviour will be ________. [2017 : 2 Marks, Set-II]
Assume the yield stress of steel as 250 MPa. The complementary strain energy (in N-mm) stored in the bar up to its linear elastic behaviour will be ________. [2017 : 2 Marks, Set-II]
Ans: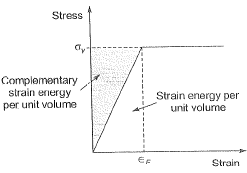 Elastic strain:
Elastic strain: 
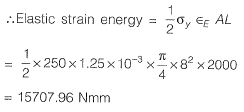
Note: For linear elastic material both complementary energy and strain energy is the same.
OR
By considering the given graph in question, between Axial Load and Displacement, the solution will be as follows: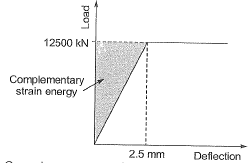 Complementary stain energy:
Complementary stain energy: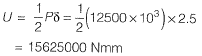
It means there seems some error in the given data.
Q14: In a material under a state of plane strain, a 10 x 10 mm square centred at a point gets deformed as shown in the figure.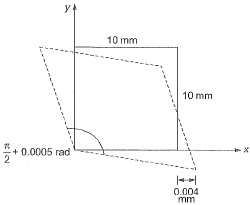 If the shear strain γxy at this point is expressed as 0.001 k (in rad), the value of k is _________. [2017 : 1 Mark, Set-II]
If the shear strain γxy at this point is expressed as 0.001 k (in rad), the value of k is _________. [2017 : 1 Mark, Set-II]
(a) 0.50
(b) 0.25
(c) -0.25
(d) -0.50
Ans: (d)
According to the sign convention: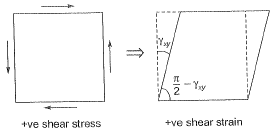 In question, since angle has been increased, therefore, shear strain should be negative.
In question, since angle has been increased, therefore, shear strain should be negative.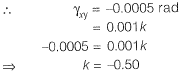
Q15: Consider the stepped bar made with a linear elastic material and subjected to an axial load of 1 kN, as shown in the figure.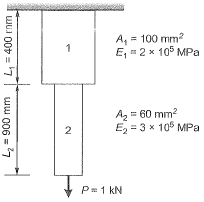 Segments 1 and 2 have a cross-sectional area of 100 mm2 and 60 mm2. Young’s modulus of 2 x 105 MPa and 3 x 105 MPa, and length of 400 mm and 900 mm, respectively. The strain energy (in N-mm up to one decimal place) in the bar due to the axial load is _________. [2017 : 2 Marks, Set-I]
Segments 1 and 2 have a cross-sectional area of 100 mm2 and 60 mm2. Young’s modulus of 2 x 105 MPa and 3 x 105 MPa, and length of 400 mm and 900 mm, respectively. The strain energy (in N-mm up to one decimal place) in the bar due to the axial load is _________. [2017 : 2 Marks, Set-I]
Ans: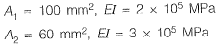
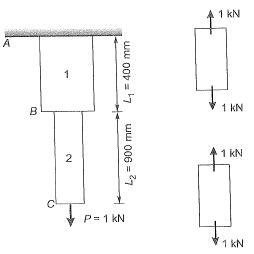
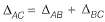
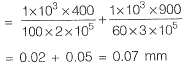
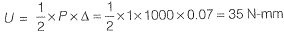
[2016 : 2 Marks, Set-II]
Q16: A tapered circular rod of diameter varying from 20 mm to 10 mm is connected to another uniform circular rod of diameter 10 mm as shown in the following figure. Both bars are made of the same material with the modulus of elasticity, E = 2 x 105 MPa. When subjected to a load P = 30πkN, the deflection at point A is ___ mm. [2015 : 2 Marks, Set-I]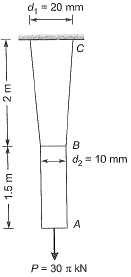 Ans:
Ans: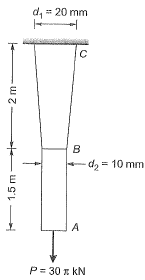 Total elongation,
Total elongation,
AB is uniform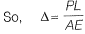
BC is tapered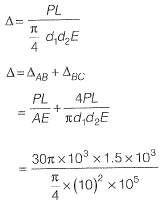
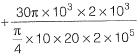
= (9 + 6) mm = 15 mm
Q17: For the state of stresses (in MPa) shown in the figure below, the maximum shear stress (in MPa) is _______.
[2014 : 2 Marks, Set-II]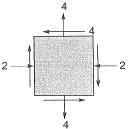 Ans:
Ans: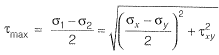
= 5.0 MPa
[2014 : 2 Marks, Set-II]
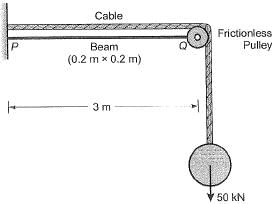

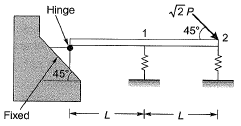
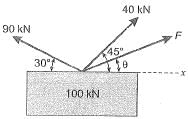
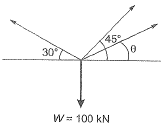
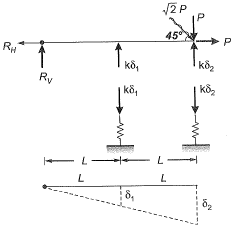
If the load Pequals 100 kN, which of the following options represents forces P1 and P2 in the springs at points ‘1’ and ‘27'?
[2011 : 2 Marks]

Which of the following options represents the deflections δ1 and δ2 at points ‘Y and ‘2’? [2011 : 2 Marks]
|
2 videos|122 docs|55 tests
|
FAQs on Past Year Questions: Properties of Metals, Stress & Strain - Civil Engineering SSC JE (Technical) - Civil Engineering (CE)
| 1. What are the main properties of metals that make them suitable for construction and manufacturing? |  |
| 2. How do stress and strain relate to the properties of metals? |  |
| 3. What is the difference between elastic and plastic deformation in metals? |  |
| 4. What factors affect the strength of metals under stress? |  |
| 5. How is the concept of yield strength important in engineering applications? |  |

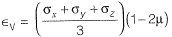
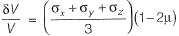
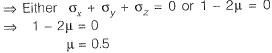

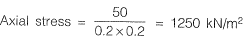
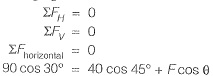
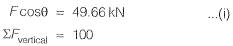
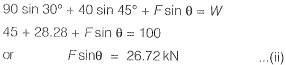
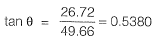
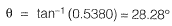
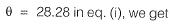
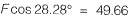
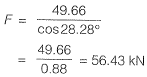

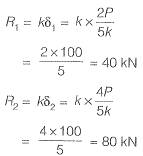
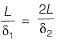
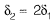 ...(i)
...(i)