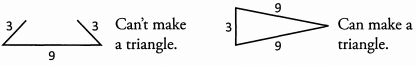Section - 1
Ques 1: The radius of a circle is 4. W hat is its area?
Ans: Area of a circle is πr2, so the area of the circle is π(4)2, which equals 16π.
Ques 2: The diameter of a circle is 7. What is its circumference?
Ans: Circumference of a circle is 2πr, or πd. We have the diameter, so the circumference equals π(7), which equals 7π.
Ques 3: The radius of a circle is 3. What is its circumference?
Ans: Circumference of a circle is 2πr, or πd. We have the radius, so circumference equals 2π(3), which equals 6π.
Ques 4: The area of a circle is 36π. What is its radius?
Ans: Area of a circle is πr2, so 36π = πr2. We need to solve for r. Divide both sides by π, so 36 = r2. Take the square root of both sides, and 6 = r. We can ignore the negative solution because distances cannot be negative.
Ques 5: The circumference of a circle is 18π. What is its area?
Ans: The connection between circumference and area is radius. We can use the circumference to solve for the radius. 18π = 2πr, which means that 9 = r. That means that Area = π(9)2 which equals 81π.
Section - 2
Ques 6: The area of a circle is 100π. What is its circumference?
Ans: The connection between circumference and area is radius. 100π = πr2, and solving for r gives us r = 10. That means that Circumference = 2π(10), which equals 20π.
Ques 7: The diameter of a circle is 16. Calculate its radius, circumference, and area.
Ans: d = 2r, so 16 = 2r. Radius = 8. Circumference = 2πr, so Circumference = 2π(8) = 16π. Area = πr2, so Area = π(8)2 = 64π.
Ques 8: Which circle has a larger area? Circle A has a circumference of 6π and Circle B has an area of 8π.
Ans: To figure out which circle has a larger area, we need to find the area of Circle A. If we know the circumference, then 6π = 2πr, which means r = 3. If r = 3, then Area = π(3)2 = 9π. 9π > 8π, so Circle A has a larger area.
Ques 9: Which has a larger area? Circle C has a diameter of 10 and Circle D has a circumference of 12π.
Ans: We need to find the area of both circles. Let’s start with Circle C. If the diameter of Circle C is 10, then the radius is 5. That means that Area = π(5)2 = 25π.
If the circumference of Circle D is 12π , the 12π = 2πr. r = 6. If r = 6, then Area = π(6)2 = 36π. 36π > 25π, so Circle D has the larger area.
Section - 3
Ques 10: A sector has a central angle of 90°. If the sector has a radius of 8, w hat is the area of the sector?
Ans: If the sector has a central angle of 90°, then the sector is 1/4 of the circle, because 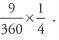
To find the area of the sector, we need to find the area of the whole circle first. The radius is 8, which means the area is π(8)2 = 64π. 1/4 x 64π = 16π. The area of the sector is 16π.
Ques 11: A sector has a central angle of 30°. If the sector has a radius of 6, what is the arc length of the sector?
Ans: If the sector has a central angle of 30°, then it is 1/12th of the circle, because 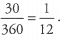 To find the arc length of the sector, we need to know the circumference of the entire circle. The radius of the circle is 6, so the circumference is 2π(6) = 12π. That means that the arc length of the sector is 1/12 x 12π = π.
To find the arc length of the sector, we need to know the circumference of the entire circle. The radius of the circle is 6, so the circumference is 2π(6) = 12π. That means that the arc length of the sector is 1/12 x 12π = π.
Ques 12: A sector has an arc length of 7π and a diameter of 14. What is the central angle of the sector?
Ans: To find the central angle of the sector, we first need to find what fraction of the full circle the sector is. We have the arc length, so if we can find the circumference of the circle, we can figure out what fraction of the circle the sector is. The diameter is 14, so the circumference is π(14) = 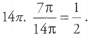 So the sector is 1/2 the full circle. That means that the central angle of the sector is 1/2 x 360° = 180°. So the central angle is 180°.
So the sector is 1/2 the full circle. That means that the central angle of the sector is 1/2 x 360° = 180°. So the central angle is 180°.
Section - 4
Ques 13: The area of a sector is 1/10th the area of the full circle. What is the central angle of the sector?
Ans: If the area of the sector is l/10th of the area of the full circle, then the central angle will be l/10th of the degree measure of the full circle. 1/10 x 360 = 36, so the central angle of the sector is 36°.
Ques 14: What is the perimeter of a sector with a radius of 5 and a central angle of 72°?
Ans: To find the perimeter of a sector, we need to know the radius of the circle and the arc length of the sector.
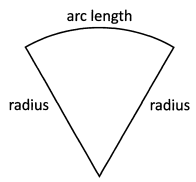
We know the radius is 5, so now we need to find the arc length. Lets begin by determining.
what fraction of the circle the sector is. The central angle of the sector is 72°, so the sector is l/5th of the circle, because 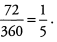 Now we need to find the circumference. The radius is 5, so the circumference of the circle is 2π(5) = 10π. The arc length of the sector is l/5th the circumference. 1/5 x 10π = 2π. So now our sector looks like this. The perimeter of the sector is 10 + 2π.
Now we need to find the circumference. The radius is 5, so the circumference of the circle is 2π(5) = 10π. The arc length of the sector is l/5th the circumference. 1/5 x 10π = 2π. So now our sector looks like this. The perimeter of the sector is 10 + 2π.
Ques 15: A sector has a radius of 8 and an area of 8π. What is the arc length of the sector?
Ans: We first need to find what fraction of the circle the sector is. We can do this by comparing areas. The radius of the circle is 8, so the area of the circle is π(8)2 = 64π. That means the sector is l/8th of the circle, because . If we want to find the arc length of the sector, we need to know the circumference. The radius is 8, so the circumference is 2π(8) = 16π. The sector is l/8th of the circle, so the arc length will be l/8th of the circumference. 1/8 x 16π = 2π. The arc length of the sector is 2π .
Section - 5
Ques 16: A triangle has two sides with lengths of 5 and 11, respectively. W hat is the range of values for the length of the third side?
Ans: The lengths of any two sides of a triangle must add up to greater than the length of the third side. The third side must be less than 5 + 11 = 16. It must also be greater than 11 -5 = 6. Therefore, 6 < third side < 16.
Ques 17: In a right triangle, the length of one of the legs is 3 and the length of the hypotenuse is 5. What is the length of the other leg?
Ans: If you know the lengths of two sides of a right triangle, you can use the Pythagorean Theorem to solve for the length of the third side. Remember that the hypotenuse must be the side labeled c in the equation a2 + b2 = c2. That means that (3)2 + (b)2 = (5)2. 9 + b2 = 25. b2 = 16, so b = 4.
Alternatively, you can recognize the Pythagorean triplet. This is a 3 -4 -5 triangle.
Ques 18: What is the area of Triangle DEF?
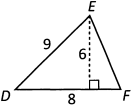
Ans: The area of a triangle is 1/2 base x height. Remember that the base and the height must be perpendicular to each other. That means that in Triangle DEF, side DF can act as the base, and the line dropping straight down from point E to touch side DF at a right angle can act as the base. Therefore Area = 1/2 (8) x (6) = 24.
Ques 19: Which side of Triangle GHI has the longest length?
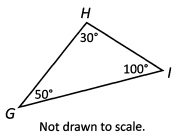
Ans: Although GI looks like the longest side, remember that you can’t trust what the picture looks like when the question states the picture is not drawn to scale. In any triangle, the longest side will be opposite the larger angle. Angle GIH is the largest angle in the triangle, and side GH is thus the longest side.
Section - 6
Ques 20: Two sides of a triangle have lengths 4 and 8. Which of the following are possible side lengths of the third side? (More than one may apply)
a. 2
b .4
c. 6
d .8
Ans: The lengths of any two sides of a triangle must add up to greater than the length of the third side. The third side must be less than 4 + 8 = 12 and greater than 8 - 4 = 4. So 4 < third side < 12. Only choices c. and d. are in that range.
Ques 21: DFG is a straight line. W hat is the value of x?
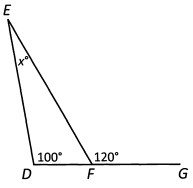
Ans: To find the value of x, we need to find the degree measures of the other two angles in Triangle DEF. We can make use of the fact that DFG is a straight line. Straight lines have a degree measure of 180, so angle DFE + 120 = 180, which means angle DFE = 60.
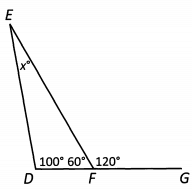
Now we can solve for x, because 100 + 60 + x = 180. Solving for x , we get x = 20.
Ques 22: Isosceles triangle ABC has two sides with lengths 3 and 9. What is the length of the third side?
Ans: It may at first appear like we don’t have enough information to answer this question. If all we know is that the triangle is isosceles, then all we know is that two sides have equal length, which means the third side has a length of either 3 or 9. But if the third side were 3, then the lengths of two of the sides would not add up to greater than the length of the third side, because 3 + 3 is not greater than 9.
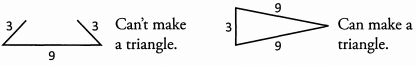
That means that the length of the third side must be 9.
Section - 7
Ques 23: What is the perimeter of triangle ABC?
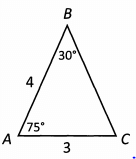
Ans: To find the perimeter of Triangle ABC, we need the lengths of all 3 sides. There is no immediately obvious way to find the length of side BC, so lets see what inferences we can make from the information the question gave us.
We know the degree measures of two of the angles in Triangle ABC, so we can find the degree measure of the third. We’ll label the third angle x. We know that 30 + 75 + x = 180. Solving for x we find that x = 75.
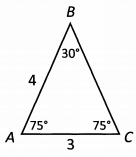
Angle BAC and angle BCA are both 75, which means Triangle ABC is an isosceles triangle. If those two angles are equal, we know that their opposite sides are also equal. Side AB has a length of 4, so we know that BC also has a length of 4.
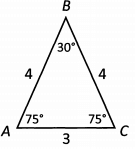
To find the perimeter, we add up the lengths of the three sides. 4 + 4 + 3=11.
Ques 24: The area of right triangle ABC is 15. W hat is the length of hypotenuse BC?
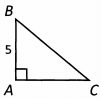
Ans: To find the length of the hypotenuse, we need the lengths of the other two sides. Then we can use the Pythagorean Theorem to find the length of the hypotenuse. We can use the area formula to find the length of AC. Area = 1/2 base x height, and we know the area and the height. So 15 = 1/2 (base) x (5). When we solve this equation, we find that the base = 6.
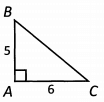
Now we can use the Pythagorean Theorem. (5)2 + (6)2 = c2. 25 + 36 = c2. 61 = c2. √61 = c . Since 61 is not a perfect square, we know that c will be a decimal. 61 is also prime, so we cannot simplify √61 any further. (It will be a little less than √64 = 8 .)
Ques 25: What is the length of side HI?
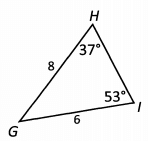
Ans: There is no immediately obvious way to find the length of side HI, so lets see what we can infer from the picture. We know two of the angles of Triangle GHI, so we can find the third. We’ll label the third angle x. 37 + 53 + x = 180. That means x = 90. So really our triangle looks like this:
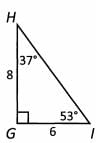
You should definitely redraw once you discover the triangle is a right triangle!
Now that we know Triangle GHIis a right triangle, we can use the Pythagorean Theorem to find the length of HI. H I is the hypotenuse, so (6)2 + (8)2 = c2. 36 + 64 = c2. 100 = c2. 10 = c. The length of HI is 10.
Alternatively, we could have recognized the Pythagorean triplet. Triangle GHI is a 6 -8-10 triangle.
Section - 8
Ques 26: What is the perimeter of parallelogram ABCD?
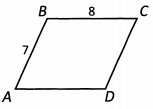
Ans: Opposite sides of a parallelogram are equal, so we know that side CD has a length of 7 and side AD has a length of 8. So the perimeter is 7 + 8 + 7 + 8 = 30.
Alternatively, the perimeter is 2 x (7 + 8) = 30. We can say this because we know that 2 sides have a length of 7 and 2 sides have a length of 8.
Ques 27: What is the area of parallelogram EFGH?
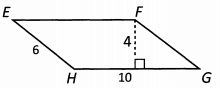
Ans: The area of a parallelogram is base x height. In this parallelogram, the base is 10 and the height is 4 (remember, base and height need to be perpendicular). So the area is 10 x 4 = 40.
Ques 28: The two parallelograms pictured below have the same perimeter. W hat is the length of side EH?
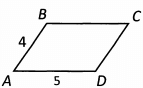
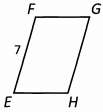
Ans: First we can find the perimeter of Parallelogram ABCD. We know that 2 sides have a length of 4, and 2 sides have a length of 5. The perimeter is 2 x (4 + 5) = 18. That means Parallelogram EFGH also has a perimeter of 18. We know side GH also has a length of 7. We don’t know the lengths of the other 2 sides, but we know they have the same length, so for now let’s say the length of each side is x. Our parallelogram now looks like this:
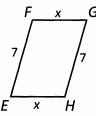
So we know that 7 + x + 7 + x = 18 → 2x + 14 = 18 → 2x = 4 → x = 2
The length of side EH is 2.
Section - 9
Ques 29: What is the area of Rectangle ABCD?
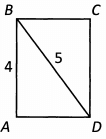
Ans: To find the area of Rectangle ABCD, we need to know the length of AD or BC. In a rectangle, every internal angle is 90 degrees, so Triangle ABD is actually a right triangle. That means we can use the Pythagorean Theorem to find the length of side AD. Actually, this right triangle is one of the Pythagorean Triplets— a 3 -4 -5 triangle. The length of side AD is 3. That means the area of Rectangle ABCD is 3 x 4 = 12.
Ques 30: In Rectangle ABCD, the area of Triangle ABC is 30. What is the length of diagonal AC?
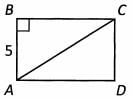
Ans: We know the area of Triangle ylSC and the length of side AB. Because side BC is perpendicular to side AB, we can use those as the base and height of Triangle ABC. So we know that 1/2(5) x (BC) = 30. That means the length of side BC is 12.
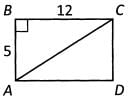
Now we can use the Pythagorean Theorem to find the length of diagonal AC, which is the hypotenuse of right triangle ABC. We can also recognize that this is a Pythagorean Triplet — a 5 - 12 - 13 triangle. The length of diagonal AC is 13.
Ques 31: Rectangles ABCD and EFGH have equal areas. W hat is the length of side FG?
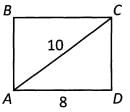

Ans: The first thing to notice in this problem is that we can find the length of side CD. Triangle ACD is a right triangle, and we know the lengths of two of the sides. We can either use the Pythagorean Theorem or recognize that this is one of our Pythagorean Triplets— a 6 - 8 - 10 triangle. The length of side CD is 6. Now we can find the area of Rectangle ABCD. Side AD is the length and side CD is the width.
8 x 6 = 48.
That means that the area of Rectangle EFGH is also 48. We can use the area and the length of side EF to solve for the length of side FG. 12 x (FG) = 48. The length of side FG is 4.
Section - 10
Ques 32: What is the perimeter of a square with an area of 25?
Ans: A square has four equal sides, so the area of a square is the length of one side squared. That means the lengths of the sides of the square are 5. If each of the four sides has a length of 5, then the perimeter is 4 x (5) = 20.
Ques 33: A rectangle and a square have the same area.The square has a perimeter of 32 and the rectangle has a length of 4. W hat is the width of the rectangle?
Ans: We should start by drawing the shapes that they describe.
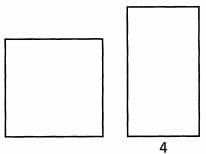
The square has four equal sides, so that means that the perimeter is 4 times the length of one side. If we designate the length of the sides of the square s, then the perimeter is 4s = 32. That means that s is 8. Now that we know the length of the sides, we can figure out the area of the square. Area = 82. So the area of the square is 64.
That means that the area of the rectangle is also 64. We know the length of the rectangle is 4, so we can solve for the width. 4 x (width) = 64. The width is 16.
Ques 34: A circle is inscribed inside a square, so that the circle touches all four sides of the square. The length of one of the sides of the square is 9. What is the area of the circle?
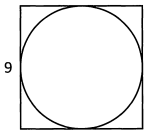
Ans: We need to find a common link between the square and the circle, so that we can find the area of the circle. We know that the length of the sides of the square is 9. We can draw a new line in our figure that has the same length as the sides AND is the diameter of the circle. That means that the diameter of the circle is 9. If the diameter is 9, then the radius is 4.5. That means the area of the circle is π(4.5)2, which equals 20.25π.
Section - 11
Ques 35: Draw a coordinate plane and plot the following points:
1 .(2 ,3 )
2. (- 2 ,- 1 )
3. (- 5 ,- 6 )
4. (4 ,-2 .5 )
Ans:
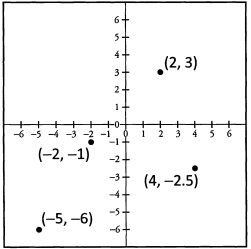
Ques 36: What are the x- and y-coordinates of the following points?
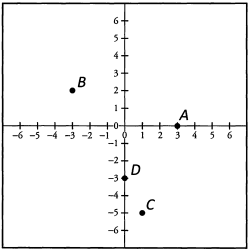
Ans: A: (3,0) B :(-3 ,2 ) C: (1, -5) D: (0,-3)
Ques 37: What is they-coordinate of the point on the line that has an x-coordinate of 3?
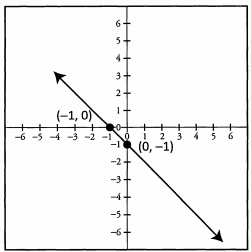
Ans: The y-coordinate of the point on the line that has an x-coordinate of 3 is -4 . The point is (3, -4). If you want, you can determine that the line has a slope of-1 from the two labeled points that the line intercepts, (-1, 0) and (0, -1).
Section - 12
Ques 38: Does the point (-3 ,0 ) lie on the curve y = x2 - 3?
Ans: For the point (-3, 0) to lie on the curvey = x2 - 3, y needs to equal 0 when we plug in -3 for x.
y = (-3)2 - 3
y = 9 - 3 = 6
y does not equal 0 when x equals - 3, so the point does not lie on the curve.
Ques 39: For the line y = 4x + 2, what is the y-coordinate when x = 3?
Ans: y = 4(3) + 2
7 = 12 + 2 = 14
The y-coordinate is 14. The point is (3, 14).
Ques 40: What is the y-intercept of the line y = -2 x - 7?
Ans: The equation of the line is already in y = mx + b form, and b stands for the y-intercept, so we just need to look at the equation to find the y-intercept. The equation is y = -2x - 7. That means the y-intercept is -7 The point is (0, -7).
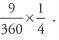
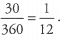 To find the arc length of the sector, we need to know the circumference of the entire circle. The radius of the circle is 6, so the circumference is 2π(6) = 12π. That means that the arc length of the sector is 1/12 x 12π = π.
To find the arc length of the sector, we need to know the circumference of the entire circle. The radius of the circle is 6, so the circumference is 2π(6) = 12π. That means that the arc length of the sector is 1/12 x 12π = π.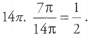 So the sector is 1/2 the full circle. That means that the central angle of the sector is 1/2 x 360° = 180°. So the central angle is 180°.
So the sector is 1/2 the full circle. That means that the central angle of the sector is 1/2 x 360° = 180°. So the central angle is 180°.
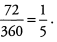 Now we need to find the circumference. The radius is 5, so the circumference of the circle is 2π(5) = 10π. The arc length of the sector is l/5th the circumference. 1/5 x 10π = 2π. So now our sector looks like this. The perimeter of the sector is 10 + 2π.
Now we need to find the circumference. The radius is 5, so the circumference of the circle is 2π(5) = 10π. The arc length of the sector is l/5th the circumference. 1/5 x 10π = 2π. So now our sector looks like this. The perimeter of the sector is 10 + 2π.