RD Sharma Solutions (Part - 1) - Ex-14.1, Lines and Angles, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Write down each pair of adjacent angles shown in Fig.
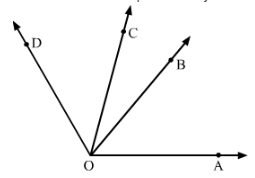
Answer 1:
Adjacent angles are the angles that have a common vertex and a common arm.
Following are the adjacent angles in the given figure:
∠DOC and ∠BOC
∠COB and ∠BOA
Question 2:
In Fig., name all the pairs of adjacent angles.
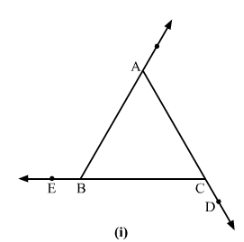
Answer 2:
In figure (i), the adjacent angles are:
∠EBA and∠ABC
∠ACB and ∠BCF
∠BAC and ∠CAD
In figure (ii), the adjacent angles are:
∠∠BAD and ∠∠DAC
∠∠BDA and ∠∠CDA
Question 3:
In figure, write down: (i) each linear pair (ii) each pair of vertically opposite angles.
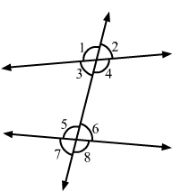
Answer 3:
(i) Two adjacent angles are said to form a linear pair of angles if their non-common arms are two opposite rays.
∠1 and ∠3
∠1 and ∠2
∠4 and ∠3
∠4 and ∠2
∠5 and ∠6
∠5 and ∠7
∠6 and ∠8
∠7 and ∠8
(ii) Two angles formed by two intersecting lines having no common arms are called vertically opposite angles.
∠1 and ∠4
∠2 and ∠3
∠5 and ∠8
∠6 and ∠7
Question 4:
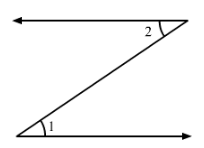
Are the angles 1 and 2 given in Fig. adjacent angles?
Answer 4:
No, because they have no common vertex.
Question 5:
Find the complement of each of the following angles:
(i) 35°
(ii) 72°
(iii) 45°
(iv) 85°
Answer 5:
Two angles are called complementary angles if the sum of those angles is 90°.
Complementary angles of the following angles are:
(i) 90°−35°=55°
(ii) 90°−72°=18°
(iii) 90°−45°=45°
(iv) 90°−85°=5°
Question 6:
Find the supplement of each of the following angles:
(i) 70°
(ii) 120°
(iii) 135°
(iv) 90°
Answer 6:
Two angles are called supplementary angles if the sum of those angles is 180°.
Supplementary angles of the following angles are:
(i) 180° − 70° = 110°
(ii) 180° − 120° = 60°
(iii) 180° − 135° = 45°
(iv) 180° − 90° = 90°
Question 7:
Identify the complementary and supplementary pairs of angles from the following pairs:
(i) 25°, 65°
(ii) 120°, 60°
(iii) 63°, 27°
(iv) 100°, 80°
Answer 7:
Since
(i) 25°+65°=90° , therefore this is complementary pair of angle.
(ii) 120°+ 60°= 180°, therefore this is supplementary pair of angle.
(iii) 63°+27°= 90°, therefore this is complementary pair of angle.
(iv) 100°+ 80°= 180° , therefore this is supplementary pair of angle.
Therefore, (i) and (iii) are the pairs of complementary angles and (ii) and (iv) are the pairs of supplementary angles.
Question 8:
Can two angles be supplementary, if both of them be
(i) obtuse?
(ii) right?
(iii) acute?
Answer 8:
(i) No, two obtuse angles cannot be supplementary.
(ii) Yes, two right angles can be supplementary. (∵∠90°+∠90°=∠180°)
(iii) No, two acute angles cannot be supplementary.
Question 9:
Name the four pairs of supplementary angles shown in Fig.

Answer 9:
Following are the supplementary angles:
∠AOC and ∠COB
∠BOC and ∠DOB
∠BOD and ∠DOA
∠AOC and ∠DOA
Question 10:
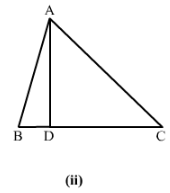
In Fig., A, B, C are collinear points and ∠DBA = ∠EBA.
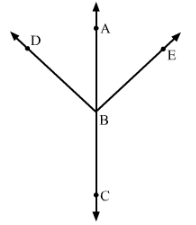
(i) Name two linear pairs
(ii) Name two pairs of supplementary angles.
Answer 10:
(i) Linear pairs:
∠ABD and ∠DBC
∠ABE and ∠EBC
Because every linear pair forms supplementary angles, these angles are:
∠ABD and ∠DBC
∠ABE and ∠EBC
Question 11:
If two supplementary angles have equal measure, what is the measure of each angle?
Answer 11:
Let x and y be two supplementary angles that are equal.
∠x=∠y
According to the question,
∠x+∠y=180°
⇒∠x+∠x=180°
⇒2∠x=180°
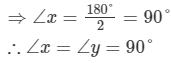
Question 12:
If the complement of an angle is 28°, then find the supplement of the angle.
Answer 12:
Let x be the complement of the given angle 28°28°.
∴ ∠x+28°=90°
⇒∠x=90°−28°=62°
So, supplement of the angle = 180°−62°=118°180°-62°=118°
Question 13:
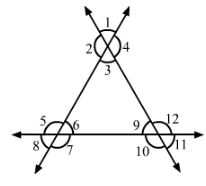
In Fig. 19, name each linear pair and each pair of vertically opposite angles:
Answer 13:
Two adjacent angles are said to form a linear pair of angles if their non-common arms are two opposite rays.
∠1 and ∠2
∠2 and ∠3
∠3 and ∠4
∠1 and ∠4
∠5 and ∠6
∠6 and ∠7
∠7 and ∠8
∠8 and ∠5
∠9 and ∠10
∠10 and ∠11
∠11 and ∠12
∠12 and ∠9
Two angles formed by two intersecting lines having no common arms are called vertically opposite angles.
∠1 and ∠3
∠4 and ∠2
∠5 and ∠7
∠6 and ∠8
∠9 and ∠11
∠10 and ∠12
Question 14:
In Fig., OE is the bisector of ∠BOD. If ∠1 = 70°, find the magnitudes of ∠2, ∠3 and ∠4.
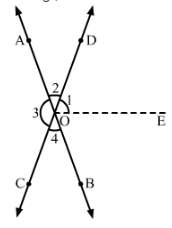
Answer 14:
Since OE is the bisector of ∠∠BOD,
∴∠DOE=∠EOB
∠2+∠1+∠EOB=180° (Linear Pair)
∠2+2∠1=180° (∠1=∠EOB)
⇒∠2=180°−2∠1=180°−2×70°=180°−140°=40°
∠4=∠2=40° (Vertically opposite angles)
∠3=∠DOB=∠1+∠EOB=70°+70°=140° [∠3=∠DOB (Vertically opposite angles)
FAQs on RD Sharma Solutions (Part - 1) - Ex-14.1, Lines and Angles, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are lines and angles in mathematics? |  |
| 2. How are lines and angles classified? |  |
| 3. What is the sum of angles in a straight line? |  |
| 4. How can angles be measured? |  |
| 5. What is the difference between an acute angle and an obtuse angle? |  |





















