RD Sharma Solutions (Part - 1) - Ex-20.1, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Find the area, in square metres, of a rectangle whose
(i) Length = 5.5 m, breadth = 2.4 m
(ii) Length = 180 cm, breadth = 150 cm
Answer 1:
We have,
(i) Length = 5.5 m, Breadth = 2.4 m
Therefore,
Area of rectangle = Length x Breadth
= 5.5 m x 2.4 m
= 13.2 m2
(ii) Length = 180 cm = 1.8 m, Breadth = 150 cm = 1.5 m [ Since 100 cm = 1 m]
Therefore,
Area of rectangle = Length x Breadth
= 1.8 m x 1.5 m
= 2.7 m2
Question 2:
Find the area, in square centimetres, of a square whose side is
(i) 2.6 cm
(ii) 1.2 dm
Answer 2:
We have,
(i) Side of the square = 2.6 cm
Therefore, area of the square = (Side)2
= (2.6 cm)2 = 6.76 cm2
(ii) Side of the square = 1.2 dm = 1.2 x 10 cm = 12 cm [ Since 1 dm = 10 cm]
Therefore, area of the square = (Side)2
= (12 cm)2 = 144 cm2
Question 3:
Find in square metres, the area of a square of side 16.5 dam.
Answer 3:
We have,
Side of the square = 16.5 dam = 16.5 x 10 m = 165 m [ Since 1 dam = 10 m ]
Area of the square = (Side)2 = (165 m)2
= 27225 m2
Question 4:
Find the area of a rectangular feild in ares whose sides are:
(i) 200 m and 125 m
(ii) 75 m 5 dm and 125 m
Answer 4:
We have,
(i) Length of the rectangular field = 200 m
Breadth of the rectangular field = 125 m
Therefore,
Area of the rectangular field = Length x Breadth
= 200 m x 125 m
= 25000 m2 = 250 ares [Since 100 m2 = 1 are]
(ii) Length of the rectangular field =75 m 5 dm = (75 + 0.5) m = 75.5 m [Since 1 dm = 10 cm = 0.1 m]
Breadth of the rectangular field = 120 m
Therefore,
Area of the rectangular field = Length x Breadth
= 75.5 m x 120 m
= 9060 m2 = 90.6 ares [Since 100 m2 = 1 are]
Question 5:
Find the area of a rectangular field in hectares whose sides are:
(i) 125 m and 400 m
(ii) 75 m 5 dm and 120 m
Answer 5:
We have,
(i) Length of the rectangular field = 125 m
Breadth of the rectangular field = 400 m
Therefore,
Area of the rectangular field = Length x Breadth
= 125 m x 400 m
= 50000 m2 = 5 hectares [Since 10000 m2 = 1 hectare]
(ii) Length of the rectangular field =75 m 5 dm = (75 + 0.5) m = 75.5 m [Since 1 dm = 10 cm = 0.1 m]
Breadth of the rectangular field = 120 m
Therefore,
Area of the rectangular field = Length x Breadth
= 75.5 m x 120 m
= 9060 m2 = 0.906 hectares [Since 10000 m2 = 1 hectare]
Question 6:
A door of dimensions 3 m × 2m is on the wall of dimension 10 m × 10 m. Find the cost of painting the wall if rate of painting is Rs 2.50 per sq. m.
Answer 6:
We have,
Length of the door = 3 m
Breadth of the door = 2 m
Side of the wall = 10 m
Area of the wall = Side x Side = 10 m x 10 m = 100 m2
Area of the door = Length x Breadth = 3 m x 2 m = 6 m2
Thus,
Required area of the wall for painting = Area of the wall − Area of the door = (100 − 6 ) m2 = 94 m2
Rate of painting per square metre = Rs. 2.50
Hence, the cost of painting the wall = Rs. (94 x 2.50) = Rs. 235
Question 7:
A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is bent in the shape of a square, what will be the measure of each side. Also, find which side encloses more area?
Answer 7:
We have,
Perimeter the of rectangle = 2(Length + Breadth)
= 2(40 cm + 22 cm) = 124 cm
It is given that the wire which was in the shape of a rectangle is now bent into a square.
Therefore, the perimeter of the square = Perimeter of the rectangle
=> Perimeter of the square = 124 cm
⇒ 4 x side = 124 cm
∴ Side = 124/4=31 cm
Now,
Area of the rectangle = 40 cm x 22 cm = 880 cm2
Area of the square = (Side)2 = (31 cm)2 = 961 cm2
Therefore, the square-shaped wire encloses more area.
Question 8:
How many square metres of glass will be required for a window, which has 12 panes, each pane measuring 25 cm by 16 cm?
Answer 8:
We have,
Length of the glass pane = 25 cm
Breadth of the glass pane = 16 cm
Area of one glass pane = 25 cm x 16 cm = 400 cm2 = 0.04 m2 [ Since 1 m2 = 10000 cm2 ]
Thus,
Area of 12 such panes = 12 x 0.04 = 0.48 m2
Question 9:
A marble tile measures 10 cm × 12 cm. How many tiles will be required to cover a wall of size 3 m × 4 m? Also, find the total cost of the tiles at the rate of Rs 2 per tile.
Answer 9:
We have,
Area of the wall = 3 m x 4 m = 12 m2
Area of one marble tile = 10 cm x 12 cm = 120 cm2 = 0.012 m2 [ Since 1 m2 = 10000 cm2 ]
Thus,
Number of tiles = 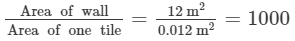
Cost of one tile = Rs. 2
Total cost = Number of tiles x Cost of one tile
= Rs. (1000 x 2) = Rs. 2000
FAQs on RD Sharma Solutions (Part - 1) - Ex-20.1, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What is RD Sharma Solutions? |  |
| 2. What is the significance of studying Mensuration - I in Class 7? |  |
| 3. How can RD Sharma Solutions help in understanding Mensuration - I? |  |
| 4. Can RD Sharma Solutions be used as a standalone study material for Mensuration - I? |  |
| 5. Are RD Sharma Solutions helpful for exam preparation in Class 7? |  |

















