RD Sharma Solutions (Part - 1) - Ex-23.1, Data Handling II Central Values, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Ashish studies for 4 hours, 5 hours and 3 hours on three consecutive days. How many hours does he study daily on an average?
Answer 1:
Average number of study hours = ( 4 + 5 + 3) ÷ 3
= 12 ÷ 3
Thus, Ashish studies for 4 hours on an average.
Question 2:
A cricketer scores the following runs in 8 innings: 58, 76, 40, 35, 48, 45, 0, 100. Find the mean score.
Answer 2:
We have:
The mean score = 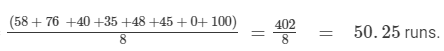
Thus, the mean score of the cricketer is 50.25 runs.
Question 3:
The marks (out of 100) obtained by a group of students in science test are 85, 76, 90, 84, 39, 48, 56, 95, 81 and 75. Find the
(i) highest and the lowest marks obtained by the students.
(ii) range of marks obtained.
(iii) mean marks obtained by the group.
Answer 3:
In order to find the highest and lowest marks, let us arrange the marks in ascending order as follows:
39, 48, 56, 75, 76, 81, 84, 85, 90, 95
(i) Clearly, the highest mark is 95 and the lowest is 39.
(ii) The range of the marks obtained is: ( 95 - 39) = 56.
(iii) We have:
Mean marks = Sum of the marks ÷÷ Total number of students
⇒ Mean marks = 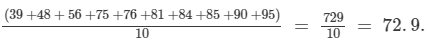
Hence, the mean marks of the students is 72.9.
Question 4:
The enrolment of a school during six consecutive years was as follows:
1555, 1670, 1750, 2019, 2540, 2820
Find the mean enrollment of the school for this period.
Answer 4:
The mean enrolment = Sum of the enrolments in each year ÷÷ Total number of years
The mean enrolment = 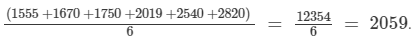
Thus, the mean enrolment of the school for the given period is 2059.
Question 5:
The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:
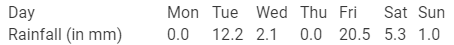
(i) Find the range of the rainfall from the above data.
(ii) Find the mean rainfall for the week.
(iii) On how many days was the rainfall less than the mean rainfall.
Answer 5:
(i) The range of the rainfall = Maximum rainfall - Minimum rainfall
= 20.5 - 0.0
= 20.5 mm .
(ii) The mean rainfall = 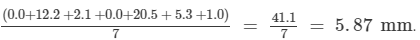
(iii) Clearly, there are 5 days (Mon, Wed, Thu, Sat, and Sun), when the rainfall was less than the mean, i.e., 5.87 mm.
Question 6:
If the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively, find the mean height.
Answer 6:
The mean height = Sum of the heights ÷÷ Total number of persons
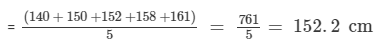
Thus, the mean height of 5 persons is 152.2 cm.
Question 7:
Find the mean of 994, 996, 998, 1002 and 1000.
Answer 7:
Mean = Sum of the observations ÷÷ Total number of observations
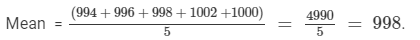
Question 8:
Find the mean of first five natural numbers.
Answer 8:
The first five natural numbers are 1, 2, 3, 4 and 5. Let 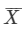 denote their arithmetic mean. Then,
denote their arithmetic mean. Then,
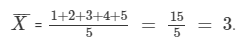
Question 9:
Find the mean of all factors of 10.
Answer 9:
The factors of 10 are 1, 2, 5 and 10 itself. Let 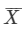 denote their arithmetic mean. Then,
denote their arithmetic mean. Then,
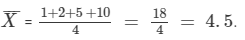
Question 10:
Find the mean of first 10 even natural numbers.
Answer 10:
The first 10 even natural numbers are 2,4, 6, 8,10,12,14,16,18 and 20. Let 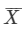 denote their arithmetic mean. Then,
denote their arithmetic mean. Then,
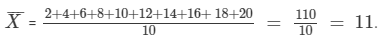
Question 11:
Find the mean of x, x + 2, x + 4, x + 6, x + 8.
Answer 11:
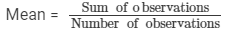
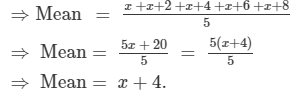
Question 12:
Find the mean of first five multiples of 3.
Answer 12:
The first five multiples of 3 are 3,6,9,12 and 15. Let 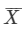 denote their arithmetic mean. Then,
denote their arithmetic mean. Then,
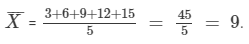
Question 13:
Following are the weights (in kg) of 10 new born babies in a hospital on a particular day:
3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean 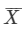
Answer 13:
We have:
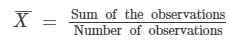
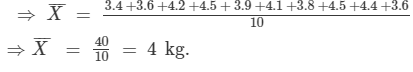
FAQs on RD Sharma Solutions (Part - 1) - Ex-23.1, Data Handling II Central Values, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are central values in data handling? |  |
| 2. How is the mean calculated in data handling? |  |
| 3. What is the median in data handling? |  |
| 4. How is the mode determined in data handling? |  |
| 5. What is the significance of central values in data handling? |  |





















