RD Sharma Solutions (Part - 1) - Ex-23.2, Data Handling II Central Values, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
A die was thrown 20 times and the following scores were recorded:
5, 2, 1, 3, 4, 4, 5, 6, 2, 2, 4, 5, 5, 6, 2, 2, 4, 5, 5, 1
Prepare the frequency table of the scores on the upper face of the die and find the mean score.
Answer 1:
The frequency table for the given data is as follows:
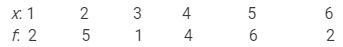
In order to compute the arithmetic mean, we prepare the following table:
Computation of Arithmetic Mean


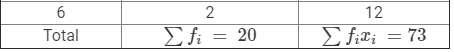
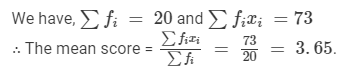
Question 2:
The daily wages (in Rs) of 15 workers in a factory are given below:
200, 180, 150, 150, 130, 180, 180, 200, 150, 130, 180, 180, 200, 150, 180
Prepare the frequency table and find the mean wage.
Answer 2:
The frequency table for the given data is as follows:
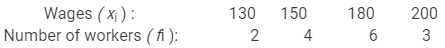
In order to compute the mean wage, we prepare the following table:
| xi | fi | fi xi |
| 130 | 2 | 260 |
| 150 | 4 | 600 |
| 180 | 6 | 1080 |
| 200 | 3 | 600 |
| Total | 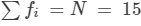 | 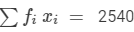 |
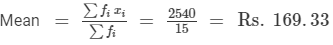
Question 3:
The following table shows the weights (in kg) of 15 workers in a factory:
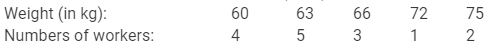
Calculate the mean weight.
Answer 3:
Calculation of Mean
Calculation of Mean
| xi | fi | fi xi |
| 60 | 4 | 240 |
| 63 | 5 | 315 |
| 66 | 3 | 198 |
| 72 | 1 | 72 |
| 75 | 2 | 150 |
| Total | 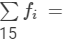 | 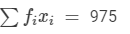 |
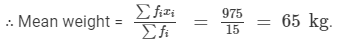
Question 4:
The ages (in years) of 50 students of a class in a school are given below:
| Age (in years): | 14 | 15 | 16 | 17 | 18 |
| Numbers of students: | 15 | 14 | 10 | 8 | 3 |
Find the mean age
Answer 4:
Calculation of Mean
| xi | fi | fi xi |
| 14 | 15 | 210 |
| 15 | 14 | 210 |
| 16 | 10 | 160 |
| 17 | 8 | 136 |
| 18 | 3 | 54 |
| Total | 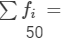 | 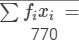 |
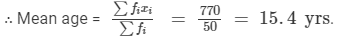
Question 5:
Calculate the mean for the following distribution:
| x : | 5 | 6 | 7 | 8 | 9 |
| f : | 4 | 8 | 14 | 11 | 3 |
Answer 5:
Calculation of Mean
| xi | fi | fi xi |
| 5 | 4 | 20 |
| 6 | 8 | 48 |
| 7 | 14 | 98 |
| 8 | 11 | 88 |
| 9 | 3 | 27 |
| Total | 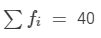 | 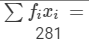 |
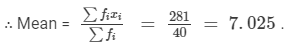
Question 6:
Find the mean of the following data:
| x: | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
| f: | 13 | 15 | 16 | 18 | 16 | 15 | 13 |
Answer 6:
Calculation of Mean
| xi | fi | fixi |
| 19 | 13 | 247 |
| 21 | 15 | 315 |
| 23 | 16 | 368 |
| 25 | 18 | 450 |
| 27 | 16 | 432 |
| 29 | 15 | 435 |
| 31 | 13 | 403 |
| Total | 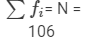 |  |
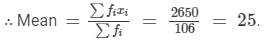
Question 7:
The mean of the following data is 20.6. Find the value of p.
| x: | 10 | 15 | p | 25 | 35 |
| f: | 3 | 10 | 25 | 7 | 5 |
Answer 7:
Calculation of Mean
| xi | fi | fi xi |
| 10 | 3 | 30 |
| 15 | 10 | 150 |
| p | 25 | 25p |
| 25 | 7 | 175 |
| 35 | 5 | 175 |
| Total | 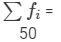 | 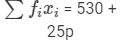 |
We have:
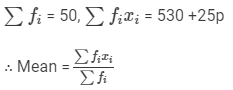
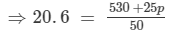
⇒20.6×50 = 530 +25p ⇒1030 = 530 +25p
⇒1030 − 530 = 25p ⇒500 = 25p
⇒p = 500/25 ⇒ p = 20
Question 8:
If the mean of the following data is 15, find p.
| x: | 5 | 10 | 15 | 20 | 25 |
| f: | 6 | p | 6 | 10 | 5 |
Answer 8:
Calculation of Mean
| xi | fi | fi xi |
| 5 | 6 | 30 |
| 10 | p | 10p |
| 15 | 6 | 90 |
| 20 | 10 | 200 |
| 25 | 5 | 125 |
| Total | 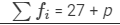 | 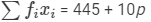 |
We have:
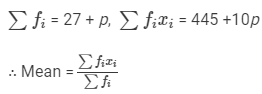
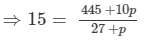
⇒15 (27 +p) = 445 +10p ⇒405 + 15p =445 +10p
⇒15p − 10p = 445 −405 ⇒5p = 40 ⇒p = 40÷5
Therefore, p = 8.
Question 9:
Find the value of p for the following distribution whose mean is 16.6
| x: | 8 | 12 | 15 | p | 20 | 25 | 30 |
| f: | 12 | 16 | 20 | 24 | 16 | 8 | 4 |
Answer 9:
Calculation of Mean
| xi | fi | fixi |
| 8 | 12 | 96 |
| 12 | 16 | 192 |
| 15 | 20 | 300 |
| p | 24 | 24p |
| 20 | 16 | 320 |
| 25 | 8 | 200 |
| 30 | 4 | 120 |
| Total | 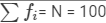 | 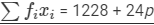 |
We have:
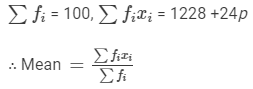
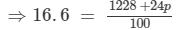
⇒16.6×100 = 1228 +24p
⇒1660 = 1228 +24p
⇒1660 − 1228 = 24p
⇒432 = 24p
⇒p = 432/24
⇒p =18
Question 10:
Find the missing value of p for the following distribution whose mean is 12.58
| x: | 5 | 8 | 10 | 12 | p | 20 | 25 |
| f: | 2 | 5 | 8 | 22 | 7 | 4 | 2 |
Answer 10:
Calculation of Mean
| xi | fi | fixi |
| 5 | 2 | 10 |
| 8 | 5 | 40 |
| 10 | 8 | 80 |
| 12 | 22 | 264 |
| p | 7 | 7p |
| 20 | 4 | 80 |
| 25 | 2 | 50 |
| Total | 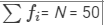 | 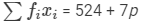 |
We have:
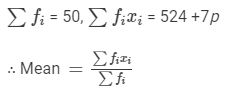
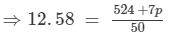
⇒12.58×50 = 524 +7p
⇒629 = 524 +7p
⇒629 − 524 = 7p
⇒105 = 7p
⇒p = 105/ 7
⇒p =15.
Question 11:
Find the missing frequency (p) for the following distribution whose mean is 7.68
| x: | 3 | 5 | 7 | 9 | 11 | 13 |
| f: | 6 | 8 | 15 | p | 8 | 4 |
Answer 11:
Calculation of Mean
| xi | fi | fi xi |
| 3 | 6 | 18 |
| 5 | 8 | 40 |
| 7 | 15 | 105 |
| 9 | p | 9p |
| 11 | 8 | 88 |
| 13 | 4 | 52 |
| Total | 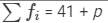 | 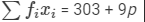 |
We have:
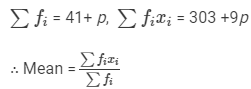
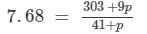
⇒7.68 × (41 +p) =303 +9p
⇒314.88 + 7.68p = 303 +9p
⇒314.88 −303 = 9p −7.68p
⇒11.88 = 1.32p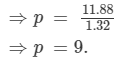
Question 12:
Find the value of p, if the mean of the following distribution is 20
| x: | 15 | 17 | 19 | 20 + p | 23 |
| f: | 2 | 3 | 4 | 5 p | 6 |
Answer 12:
Calculation of Mean
| xi | fi | fi xi |
| 15 | 2 | 30 |
| 17 | 3 | 51 |
| 19 | 4 | 76 |
| 20 + p | 5p | (20+p)5p |
| 23 | 6 | 138 |
| Total | 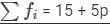 | 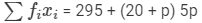 |
We have:
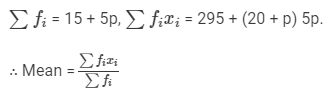
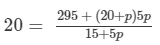
⇒20 × (15 +5p) =295 + (20+p)5p⇒300+ 100p = 295 +100p + 5p
⇒ 300 - 295 + 100p -100p = 5p2
⇒ 5 = 5p2
⇒ p2 = 1
FAQs on RD Sharma Solutions (Part - 1) - Ex-23.2, Data Handling II Central Values, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are central values in data handling? |  |
| 2. How is the mean calculated for a set of data? |  |
| 3. What is the median value in data handling? |  |
| 4. How is the mode determined in data handling? |  |
| 5. Why are central values important in data handling? |  |

|
Explore Courses for Class 7 exam
|

|

















