RD Sharma Solutions (Part - 1) - Ex - 9.1, Ratio And Proportion, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
If x : y = 3 : 5, find the ratio 3x + 4y : 8x + 5y.
Answer 1:
It is given that
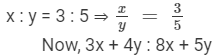
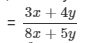
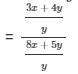 {dividing the numerator and the denominator by 'y'}
{dividing the numerator and the denominator by 'y'}
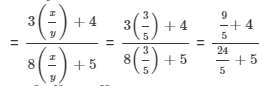
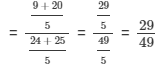
Question 2:
If x : y = 8 : 9, find the ratio (7x − 4y) : 3x + 2y.
Answer 2:
It is given that
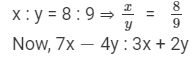
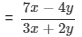
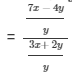 {dividing the numerator and the denominator by 'y'}
{dividing the numerator and the denominator by 'y'}
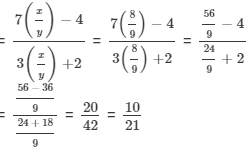
Hence, 7x −- 4y : 3x + 2y = 10 : 21.
Question 3:
If two numbers are in the ratio 6 : 13 and their l.c.m. is 312, find the numbers.
Answer 3:
Let the two numbers be 'x' and 'y' such that x : y = 6 : 13 ⇒ x/y = 613 .
We can assume that the HCF of 'x' and 'y' is a number 'k'.
So, x = 6k, and y = 13k.
Now, the product of any two numbers 'x' and 'y' is always equal to the product of their LCM and HCF
⇒ x××y = 312 ×× k
⇒ 6k ×× 13k = 312 ×× k
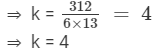
Thus, x = 6k = 6 ××4 = 24, and y = 13 ×× 4 = 52.
Question 4:
Two numbers are in the ratio 3 : 5. If 8 is added to each number, the ratio becomes 2 : 3. Find the numbers.
Answer 4:
Let the two numbers in ratio be x and y such that
x : y = 3 : 5
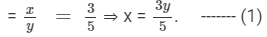
Now, 8 is added to each number, which means
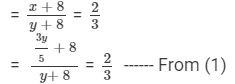
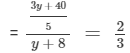
On cross-multiplying, we get
⇒ 3(3y + 40) = 2 ××5(y + 8)
⇒ 9y + 120 = 10y + 80
⇒ 120 −- 80 = 10y −- 9y
⇒ y = 40
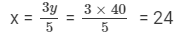
So, the numbers are 24 and 40.
Question 5:
What should be added to each term of the ratio 7 : 13 so that the ratio becomes 2 : 3
Answer 5:
Let the numbers that must be added to the ratio 7 : 13 be 'x'.
So, 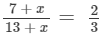
After cross-multiplication, we get
3(7 + x) = 2(13 + x)
21 + 3x = 26 + 2x
3x - 2x = 26 - 21
x = 5
Thus, 5 must be added to each term to make the ratio = 2 : 3.
Question 6:
Three numbers are in the ratio 2 : 3 : 5 and the sum of these numbers is 800. Find the numbers.
Answer 6:
We have
Sum of the terms of the ratio = 2 +3 + 5 = 10.
Sum of the numbers = 800.
Therefore, first number 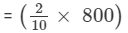
= 160
or, Second number 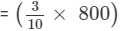
= 240
or, Third number 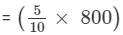
= 400
Question 7:
The ages of two persons are in the ratio 5 : 7. Eighteen years ago their ages were in the ratio 8 : 13. Find their present ages.
Answer 7:
Let the present ages of the two persons be '5x' and '7x' years.
Ratio of their present ages = 5 : 7.
Eighteen years ago, their ages were (5x −- 18) and (7x −- 18), respectively.
But eighteen years ago the ratio of their ages was 8 : 13.
So, 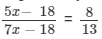
13(5x −- 18) = 8(7x −- 18)
65x −- 234 = 56x −- 144
65x −- 56x = 234 −- 144
9x = 90
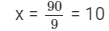
So, their ages are 5x = 5××10 = 50 years and 7x = 7 ×× 10 = 70 years.
Question 8:
Two numbers are in the ratio 7 : 11. If 7 is added to each of the numbers, the ratio becomes 2 : 3. Find the numbers.
Answer 8:
Let the two numbers be 'x' and 'y'.
Given that x : y = 7 : 11 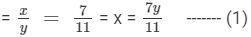
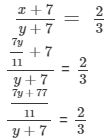
3 (7y + 77) = 2 ×× 11 (y + 7)
21y + 231 = 22y + 154
22y −- 21y = 231 −- 154
Therefore, y = 77, and x 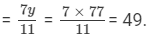
Thus, the two numbers are 49 and 77.
Question 9:
Two numbers are in the ratio 2 : 7. If the sum of the numbers is 810, find the numbers.
Answer 9:
We have
Sum of the terms of the ratio = 2 + 7 = 9.
Sum of the numbers = 810.
Therefore, first number = 2/9× 810 = 180
Second number = 7/9× 810 = 630
Question 10:
Divide Rs 1350 between Ravish and Shikha in the ratio 2 : 3.
Answer 10:
We have
Sum of the terms of the ratio = 2 + 3 = 5
Therefore, Ravish's share = Rs (25×1350)25×1350 = Rs 540
Sikha's share = Rs (3/5×1350) = Rs 810
Question 11:
Divide Rs 2000 among P, Q, R in the ratio 2 : 3 : 5.
Answer 11:
We have
Sum of the terms of the ratio = 2 +3 +5 = 10
Therefore, P's share =Rs (2/10× 2000) = Rs 400
Q's share = Rs (3/10× 2000) = Rs 600
R's share = Rs (5/10× 2000) = Rs 1000
FAQs on RD Sharma Solutions (Part - 1) - Ex - 9.1, Ratio And Proportion, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the importance of ratio and proportion in mathematics? |  |
| 2. How do you simplify ratios in mathematics? |  |
| 3. How are ratios and proportions related in mathematics? |  |
| 4. What are the different types of ratios? |  |
| 5. How can ratio and proportion be applied in real-life situations? |  |
















