RD Sharma Solutions (Part - 2)- Ex-20.2, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
QUESTION 7:
Each side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
ANSWER 7:
We have,
Side of the flower bed = 2 m 80 cm = 2.80 m [ Since 100 cm = 1 m]
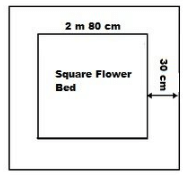
∴ Area of the square flower bed = (Side)2 = (2.80 m )2 = 7.84 m2
Side of the flower bed with the digging strip = 2.80 m + 30 cm + 30 cm
= (2.80 + 0.3 + 0.3) m = 3.4 m
Area of the enlarged flower bed with the digging strip = (Side )2 = (3.4 )2 = 11.56 m2
Thus,
Increase in the area of the flower bed = 11.56 m2 − 7.84 m2
= 3.72 m2
QUESTION 8:
A room 5 m long and 4 m wide is surrounded by a verandah. If the verandah occupies an area of 22 m2, find the width of the varandah.
ANSWER 8:
Let the width of the verandah be x m.
Length of the room AB = 5 m and BC = 4 m
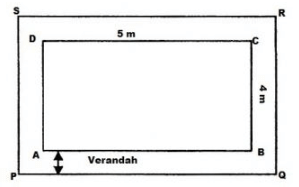
∴ Area of the room = 5 m x 4 m = 20 m2
Length of the verandah PQ = (5 + x + x) = (5 + 2x) m
Breadth of the verandah QR = ( 4 + x + x) = (4 + 2x) m
Area of verandah PQRS = (5 + 2x) x (4 + 2x) = (4x2 + 18x + 20 ) m2
∴ Area of verandah = Area of PQRS − Area of ABCD
⇒ 22 = 4x2 + 18x + 20 − 20
⇒ 22 = 4x2 + 18x
⇒ 11 = 2x2 + 9x
⇒ 2x2 + 9x − 11 = 0
⇒ 2x2 + 11x − 2x − 11 = 0
⇒ x(2x + 11) − 1(2x + 11) = 0
⇒ (x − 1) (2x +11) = 0
When x − 1 = 0, x = 1
When 2x + 11 = 0, x = −11/2
The width cannot be a negative value.
So, width of the verandah = x = 1 m.
QUESTION 9:
A square lawn has a 2 m wide path surrounding it. If the area of the path is 136 m2, find the area of the lawn.
ANSWER 9:
We have,
Let ABCD be the square lawn and PQRS be the outer boundary of the square path.
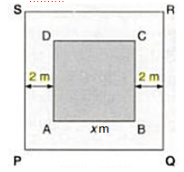
Let side of the lawn AB be x m.
Area of the square lawn = x2
Length PQ = (x m + 2 m + 2 m) = (x + 4) m
∴ Area of PQRS = (x + 4)2 = (x2 + 8x + 16) m2
Now,
Area of the path = Area of PQRS − Area of the square lawn
⇒ 136 = x2 + 8x + 16 − x2
⇒ 136 = 8x + 16
⇒ 136 − 16 = 8x
⇒ 120 = 8x
∴ x = 120 ÷ 8 = 15
∴ Side of the lawn = 15 m
Hence,
Area of the lawn = (Side)2 = (15 m)2 = 225 m2
Question 10:
A poster of size 10 cm by 8 cm is pasted on a sheet of cardboard such that there is a margin of width 1.75 cm along each side of the poster. Find (i) the total area of the margin (ii) the cost of the cardboard used at the rate of Re 0.60 per cm2.
Answer 10:
We have,
Length of the poster = 10 cm and breadth of the poster = 8 cm
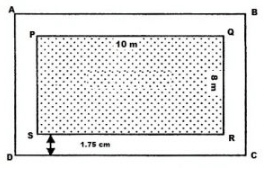
∴ Area of the poster = Length x Breadth = 10 cm x 8 cm = 80 cm2
From the figure, it can be observed that,
Length of the cardboard when the margin is included = 10 cm + 1.75 cm + 1.75 cm = 13.5 cm
Breadth of the cardboard when the margin is included = 8 cm + 1.75 cm + 1.75 cm = 11.5 cm
∴ Area of the cardboard = Length x Breadth = 13.5 cm x 11.5 cm = 155.25 cm2
Hence,
(i) Area of the margin = Area of cardboard including the margin − Area of the poster
= 155.25 cm2 − 80 cm2
= 75.25 cm2
(ii) Cost of the cardboard = Area of the cardboard x Rate of the cardboard Rs. 0.60 per cm2
= Rs. (155.25 x 0.60)
= Rs. 93.15
Question 11:
A rectangulr field is 50 m by 40 m. It has two roads through its centre, running parallel to its sides. The width of the longer and shorter roads are 1.8 m and 2.5 m respectively. Find the area of the roads and the erea of the remaining portion of the field.
Answer 11:
Let ABCD be the rectangular field and KLMN and PQRS the two rectangular roads with width 1.8 m and 2.5 m, respectively.
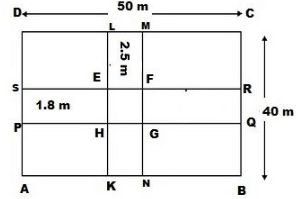
Length of the rectangular field CD = 50 cm and breadth of the rectangular field BC = 40 m
∴ Area of the rectangular field ABCD = 50 m x 40 m = 2000 m2
Area of the road KLMN = 40 m x 2.5 m = 100 m2
Area of the road PQRS = 50 m x 1.8 m = 90 m2
Clearly area of EFGH is common to the two roads.
Thus, Area of EFGH = 2.5 m x 1.8 m = 4.5 m2
Hence,
Area of the roads = Area (KLMN) + Area (PQRS) − Area (EFGH)
= (100 m2 + 90 m2) − 4.5 m2 = 185.5 m2
Area of the remaining portion of the field = Area of the rectangular field ABCD − Area of the roads
= (2000 − 185.5) m2
= 1814.5 m2
FAQs on RD Sharma Solutions (Part - 2)- Ex-20.2, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the importance of studying mensuration in Class 7 Maths? |  |
| 2. How can I calculate the area of a rectangle using mensuration? |  |
| 3. What are the different units used for measuring area and volume in mensuration? |  |
| 4. How can I calculate the volume of a cuboid using mensuration? |  |
| 5. What are the practical applications of mensuration in real life? |  |

|
Explore Courses for Class 7 exam
|

|

















