RD Sharma Solutions (Part - 2) - Ex-20.3, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 11:
Find the area of a rhombus having each side equal to 15 cm and one of whose diagonals is 24 cm.
Answer 11:
Let ABCD be the rhombus where diagonals intersect at O.
Then AB = 15 cm and AC = 24 cm.
The diagonals of a rhombus bisect each other at right angles.
Therefore, Δ AOB is a right-angled triangle, right angled at O such that
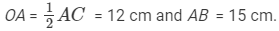
By Pythagoras theorem, we have,
(AB)2 = (OA)2 + (OB)2
⇒ (15)2 = (12)2 + (OB)2
⇒ (OB)2 = (15)2 − (12)2
⇒ (OB)2 = 225 − 144 = 81
⇒ (OB)2 = (9)2
⇒ OB = 9 cm
∴ BD = 2 x OB = 2 x 9 cm = 18 cm
Hence,
Area of the rhombus ABCD = 
Question 12:
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Answer 12:
Let ABCD be the rhombus whose diagonals intersect at O.
Then AB = 20 cm and AC = 24 cm.
The diagonals of a rhombus bisect each other at right angles.
Therefore Δ AOB is a right-angled triangle, right angled at O such that
OA = 1/2AC = 12 cm and AB = 20 cm
By Pythagoras theorem, we have,
(AB)2 = (OA)2 + (OB)2
⇒ (20)2 = (12)2 + (OB)2
⇒ (OB)2 = (20)2 − (12)2
⇒ (OB)2 = 400 − 144 = 256
⇒ (OB)2 = (16)2
⇒ OB = 16 cm
∴ BD = 2 x OB = 2 x 16 cm = 32 cm
Hence,
Area of the rhombus ABCD =
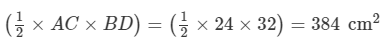
Question 13:
The length of a side of a square field is 4 m. What will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonals is 2 m?
Answer 13:
We have,
Side of a square = 4 m and one diagonal of a square = 2 m
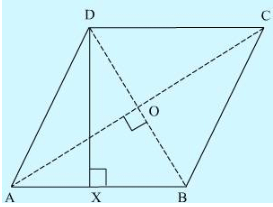
Area of the rhombus = Area of the square of side 4 m
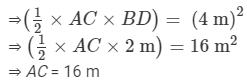
We know that the diagonals of a rhombus are perpendicular bisectors of each other.
⇒ AO=1/2AC = 8 m and BO =1/2BD=1 m
By Pythagoras theorem, we have:
AO2 + BO2 = AB2
⇒ AB2 = (8 m)2 + (1m)2 = 64 m2 + 1 m2 = 65 m2
⇒ Side of a rhombus = AB = 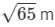
Let DX be the altitude.
Area of the rhombus = AB × DX
16 m2 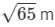 x Dx
x Dx
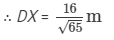
Hence, the altitude of the rhombus will be 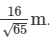
Question 14:
Two sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the sides of length 25 cm is 10 cm, find the altitude corresponding to the other pair of sides.
Answer 14:
We have,
ABCD is a parallelogram with longer side AB = 25 cm and altitude AE = 10 cm.
As ABCD is a parallelogram .hence AB=CD (opposite sides of parallelogram are equal)
The shorter side is AD = 20 cm and the corresponding altitude is CF.
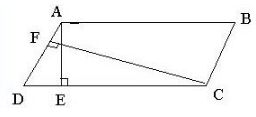
Area of a parallelogram = Base × Height
We have two altitudes and two corresponding bases.
So,
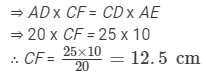
Hence, the altitude corresponding to the other pair of the side AD is 12.5 cm.
Question 15:
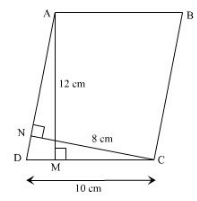
The base and corresponding altitude of a parallelogram are 10 cm and 12 cm respectively. If the other altitude is 8 cm, find the length of the other pair of parallel sides.
Answer 15:
We have,
ABCD is a parallelogram with side AB = CD = 10 cm (Opposite sides of parallelogram are equal) and corresponding altitude AM = 12 cm.
The other side is AD and the corresponding altitude is CN = 8 cm
Area of a parallelogram = Base × Height
We have two altitudes and two corresponding bases.
So,
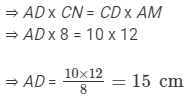
Hence, the length of the other pair of the parallel side = 15 cm.
Question 16:
A floral design on the floor of a building consists of 280 tiles. Each tile is in the shape of a parallelogram of altitude 3 cm and base 5 cm. Find the cost of polishing the design at the rate of 50 paise per cm2.
Answer 16:
We have,
Altitude of a tile = 3 cm
Base of a tile = 5 cm
Area of one tile = Altitude x Base = 5 cm x 3 cm = 15 cm2
Area of 280 tiles = 280 x 15 cm2 = 4200 cm2
Rate of polishing the tiles at 50 paise per cm2 = Rs. 0.5 per cm2
Thus,
Total cost of polishing the design = Rs. (4200 x 0.5) = Rs. 2100
FAQs on RD Sharma Solutions (Part - 2) - Ex-20.3, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the different shapes and figures covered in RD Sharma Solutions (Part - 2) for Class 7 Math? |  |
| 2. How can I find the area of a rectangle using RD Sharma Solutions (Part - 2) for Class 7 Math? |  |
| 3. What is the formula for finding the area of a triangle in RD Sharma Solutions (Part - 2) for Class 7 Math? |  |
| 4. How can I calculate the perimeter of a circle using RD Sharma Solutions (Part - 2) for Class 7 Math? |  |
| 5. Can RD Sharma Solutions (Part - 2) for Class 7 Math help me solve problems related to irregular shapes? |  |





















