RD Sharma Solutions (Part - 2) - Ex-20.4, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 11:
Calculate the area of the quadrilateral ABCD as shown in Fig. 33, given that BD = 42 cm, AC = 28 cm, OD= 12 cm and AC ⊥ BD.
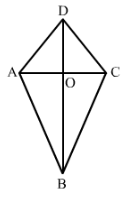
Answer 11:
We have,
BD = 42 cm, AC = 28 cm, OD = 12 cm
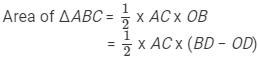
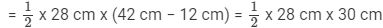
= 14 cm x 30 cm = 420 cm2
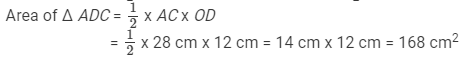
Hence,
Area of the quadrilateral ABCD = Area of Δ ABC + Area of Δ ADC
= (420 + 168) cm2 = 588 cm2
Question 12:
Find the area of a figure formed by a square of side 8 cm and an isosceles triangle with base as one side of the square and perimeter as 18 cm.
Answer 12:
Let x cm be one of the equal sides of an isosceles triangle.
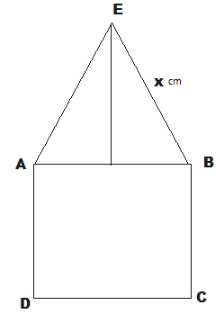
Given that the perimeter of the isosceles triangle = 18 cm
Then,
x + x + 8 = 18
⇒ 2x = (18 − 8) cm = 10 cm
⇒ x = 5 cm
Area of the figure formed = Area of the square + Area of the isosceles triangle
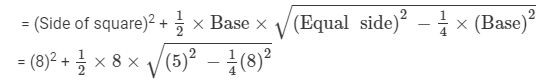
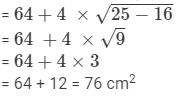
Question 13:
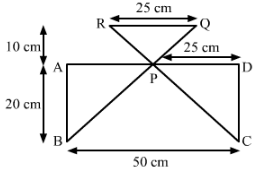
Find the area of Fig. 34 in the following ways:
(i) Sum of the areas of three triangles
(ii) Area of a rectangle − sum of the areas of five triangles
Answer 13:
We have,
(i) P is the midpoint of AD.
Thus AP = PD = 25 cm and AB = CD = 20 cm
From the figure, we observed that,
Area of Δ APB = Area of Δ PDC
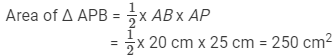
Area of Δ PDC = Area of Δ APB = 250 cm2
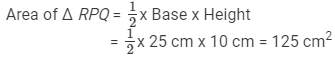
Hence,
Sum of the three triangles = (250 + 250 + 125) cm2
= 625 cm2
(ii) Area of the rectangle ABCD = 50 cm x 20 cm = 1000 cm2
Thus,
Area of the rectangle − Sum of the areas of three triangles (There is a mistake in the question; it should be area of three triangles)
= (1000 − 625 ) cm2 = 375 cm2
Question 14:
Calculate the area of quadrilateral field ABCD as shown in Fig. 35, by dividing it into a rectangle and a triangle.
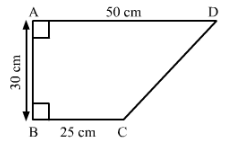
Answer 14:
We have,
Join CE, which intersect AD at point E.
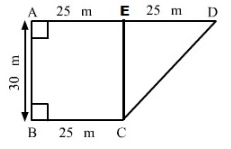
Here, AE = ED = BC = 25 m and EC = AB = 30 m
Area of the rectangle ABCE = AB x BC
= 30 m x 25 m
= 750 m2
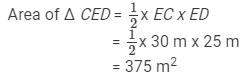
Hence,
Area of the quadrilateral ABCD = (750 + 375) m2
= 1125 m2
Question 15:
Calculate the area of the pentagon ABCDE, where AB = AE and with dimensions as shown in Fig. 36.
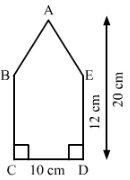
Answer 15:
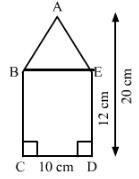
Join BE.
Area of the rectangle BCDE = CD x DE
= 10 cm x 12 cm = 120 cm2
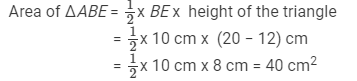
Hence,
Area of the pentagon ABCDE = (120 + 40) cm2 = 160 cm2
Question 16:
The base of a triangular field is three times its altitude. If the cost of cultivating the field at Rs 24.60 per hectare is Rs 332. 10, find its base and height.
Answer 16:
Let altitude of the triangular field be h m
Then base of the triangular field is 3h m.
Area of the triangular field = 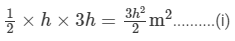
The rate of cultivating the field is Rs 24.60 per hectare.
Therefore,
Area of the triangular field = 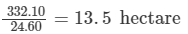
= 135000 m2 [Since 1 hectare = 10000 m2 ]..........(ii)
From equation (i) and (ii) we have,
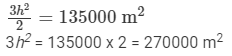
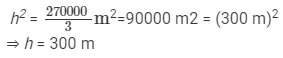
Hence,
Height of the triangular field = 300 m and base of the triangular field = 3 x 300 m = 900 m
Question 17:
A wall is 4.5 m long and 3 m high. It has two equal windows, each having form and dimensions as shown in Fig. 37. Find the cost of painting the wall (leaving windows) at the rate of Rs 15 per m2.
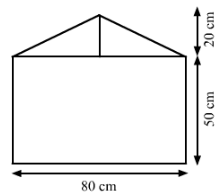
Answer 17:
We have,
Length of a wall = 4.5 m
Breadth of the wall =3 m
Area of the wall = Length x Breadth = 4.5 m x 3 m = 13.5 m2
From the figure we observed that,
Area of the window = Area of the rectangle + Area of the triangle

Area of two windows = 2 x 0.48 = 0.96 m2
Area of the remaining wall (leaving windows ) = (13.5 − 0.96 )m2 = 12.54 m2ost of painting the wall per m2 = Rs. 15
Hence, the cost of painting on the wall = Rs. (15 x 12.54) = Rs. 188.1
FAQs on RD Sharma Solutions (Part - 2) - Ex-20.4, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the importance of studying mensuration in mathematics? |  |
| 2. How can I calculate the area of a triangle? |  |
| 3. What is the formula to find the volume of a cylinder? |  |
| 4. How do I calculate the perimeter of a rectangle? |  |
| 5. What is the difference between area and volume? |  |
















