RD Sharma Solutions (Part - 2) - Ex-21.1, Mensuration - II Area of Circle, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 11:
How long will John take to make a round of a circular field of radius 21 m cycling at the speed of 8 km/hr?
Answer 11:
We have:
The radius of the circular field = 21 m
∴ Circumference of the circular field = 2πr = 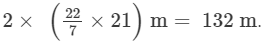
If John cycles at the speed of 8 km/hr (In 1 hour John covers 8 km = 8000 m ), then,
John covers 8000 m in 1 hour.
∴ Time required to cover 132 m = 132/8000 = 0.0165 hours
1 hour = 3600 seconds
∴ 0.0615 hours = 0.0615 x 3600 = 59.4 seconds.
Question 12:
The hour and minute hands of a clock are 4 cm and 6 cm long respectively. Find the sum of the distances travelled by their tips in 2 days.
Answer 12:
The radius of the path inscribed by the hour hand = Length of the hour hand = 4 cm
The radius of the path inscribed by the minute hand = Length of the minute hand = 6 cm
The circumference of the path inscribed by the hour hand = 2πr = 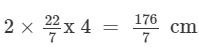
The hour hand makes 2 revolutions in one day.
∴ The distance covered by the hour hand in 2 days = 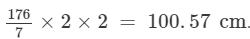
The distance covered by the minute hand in 1 revolution = 2πr = 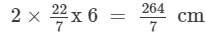
The minute hand makes 1 revolution in one hour.
∴ In 1 day, it makes 24 revolutions.
In 2 days, it makes 2 x 24 revolutions.
∴ The distance covered by the minute hand in 2 days =

The sum of the distances travelled by the hour and minute hands in 2 days = 1810.28 + 100.57 = 1910.85 cm.
Question 13:
A rhombus has the same perimeter as the circumference of a circle. If the side of the rhombus is 2.2 m, find the radius of the circle.
Answer 13:
We have:
The side of a rhombus = 2.2 m
Let C be the circumference of a circle having a radius r cm. Then,
the perimeter of the rhombus = 4×side×side = 4 x 2.2 = 8.8 m.
We know:
Perimeter of the rhombus = Circumference of the circle
⇒8.8 m = 2πr
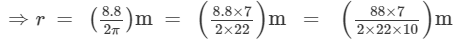
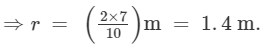
The radius of the circle is 1.4 m.
Question 14:
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
Answer 14:
We have:
The radius of the circle = 28 cm
∴ Circumference of the circle = 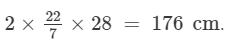
Let a cm be the side of the square. Then,
the circumference of the circle = the perimeter of the square
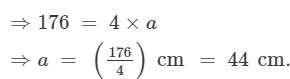
The side of the square is 44 cm.
Question 15:
A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Answer 15:
We have:
Total distance covered in 5000 revolutions = 11 km = 11,000 m
∴ Distance covered in 1 revolution = 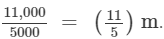
Distance covered in 1 revolution = Circumference of the wheel
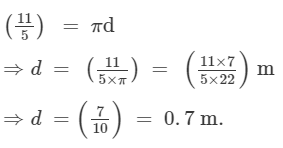
Thus, the diameter of the wheel is 0.7 m = 70 cm.
Question 16:
A boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
Answer 16:
We have:
The diameter of the wheel = 60 cm
Distance covered by the wheel in 1 revolution = Circumference of the wheel
∴ Distance covered by the wheel in 1 revolution = πd = 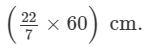
∴ Distance covered in 140 revolutions =
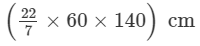
= 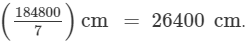
Thus, the wheel covers 26400 cm in 1 minute. Then,
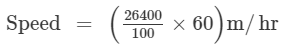 = (264×60)m/hr
= (264×60)m/hr
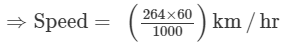 = 15.84 km/hr.
= 15.84 km/hr.
The speed with which the boy is cycling is 15.84 km/hr.
Question 17:
The diameter of the driving wheel of a bus is 140 cm. How many revolutions per minute must the wheel make in order to keep a speed of 66 km per hour?
Answer 17:
We have:
Diameter of the wheel = 140 cm, desired speed of the bus = 66 km/hr
∴ Distance covered in 1 revolution = The circumference of the wheel = πd = 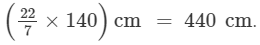
Now, the desired speed of the bus = 66 km/hr 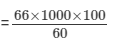 = 1,10,000 cm/min.
= 1,10,000 cm/min.
∴ Number of revolutions per minute = 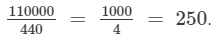
Thus, the bus must make 250 revolutions per minute to keep the speed at 66 km/hr.
Question 18:
A water sprinkler in a lawn sprays water as far as 7 m in all directions. Find the length of the outer edge of wet grass.
Answer 18:
The wet grass forms a circular region of radius 7 m.
∴ The length of the outer edge of the wet grass is 2πr = 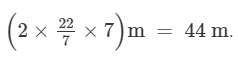
Question 19:
A well of diameter 150 cm has a stone parapet around it. If the length of the outer edge of the parapet is 660 cm, then find the width of the parapet.
Answer 19:
We have :
Diameter of the well = 150 cm
Length of the outer edge of the parapet = 660 cm
Width of the parapet = ?
Radius of well = 150 ÷ 2 = 75 cm.
Let the width of the stone parapet be x cm.Clearly, the outer edge of the parapet forms a circular region of radius (x +75 cm). Therefore,
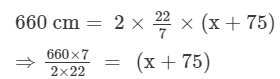
⇒15×7 = (x+75)
⇒x = 105 − 75
⇒x = 30 cm.
Thus, the width of the parapet is 30 cm.
Question 20:
An ox in a kolhu (an oil processing apparatus) is tethered to a rope 3 m long. How much distance does it cover in 14 rounds?
Answer 20:
We have :
Radius of the circular path traced by the ox in a kolhu = 3 m
Distance covered by the ox in 1 round = Circumference of the circular path =
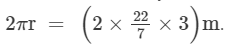
∴ Distance covered in 14 rounds = 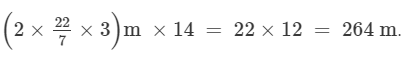
FAQs on RD Sharma Solutions (Part - 2) - Ex-21.1, Mensuration - II Area of Circle, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the formula to calculate the area of a circle? |  |
| 2. How do I find the radius of a circle if I know the area? |  |
| 3. Can I use the diameter instead of the radius to find the area of a circle? |  |
| 4. How can I find the circumference of a circle if I know the area? |  |
| 5. What is the value of π? |  |

|
Explore Courses for Class 7 exam
|

|

















