RD Sharma Solutions (Part - 2) - Ex-21.2, Mensuration - II Area of Circle, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 11:
The perimeter of a circle is 4πr cm. What is the area of the circle?
Answer 11:
We have :
Given perimeter of the circle = 4πr cm = 2π (2r) cm
We know that, the perimeter of a circle = 2ππr
∴ Radius of the circle = 2r cm
Area of the circle= πr2 = π (2r)2 = 4πr2
Question 12:
A wire of 5024 m length is in the form of a square. It is cut and made a circle. Find the ratio of the area of the square to that of the circle.
Answer 12:
We have:
Perimeter of the square = 5024 m = Circumference of the circle
⇒ 4 x Side of the square = 5024
∴ Side of the square = 5024/4 = 1256 m
Let the area of the square be A1 and the area of the circle be A2.
Area of the square (A1)= side x side = 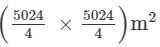
Circumference of the circle = 5024 m
⇒ 2 πr = 5024 m
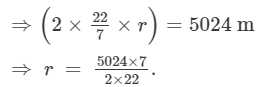
Area of the circle (A2)= πr2 = 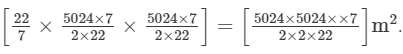
∴A1 : A2 = 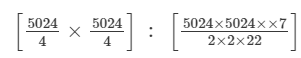
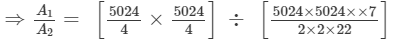
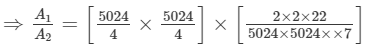
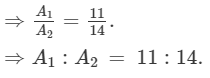
Hence, the ratio of the area of the square to the area of the circle is 11:14.
Question 13:
The radius of a circle is 14 cm. Find the radius of the circle whose area is double of the area of the circle.
Answer 13:
Let the area of the circle whose radius is 14 cm be A1.
Let the radius and area of the circle, whose area is twice the area of the circle A1 , be r2 and A2, respectively.
Thus,
A1 = π(r)2 = π(14)2 = 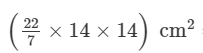 = =(44×14) cm2= 616 cm2
= =(44×14) cm2= 616 cm2
A1 = 2 × A1 = 2 × 616 = 1232 cm2
A2 = π(r2)2 = 1232 cm2
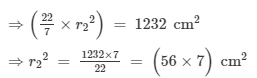
⇒r2 = 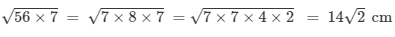
Hence, the radius of the circle A2 is 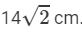
Question 14:
The radius of one circluar field is 20 m and that of another is 48 m. Find the radius of the third circular field whose area is equal to the sum of the areas of two fields.
Answer 14:
Let the area of the circle whose radius is 20 m be A1 , and the area of the circle whose radius
is 48 m be A2. Let A3 be the area of a circle that is equal to the sum of the areas of the two fields, with the radius of its field being r cm.
∴ A3 = A1 + A2
A1 = π(20)2 = 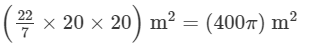
A2 = π (48)2 = 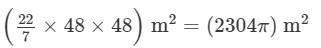
A3 = A1+A2 = (400π) +(2304π) = π(400 +2304) m2
⇒A3 = π(r)2 = π(400 +2304) m2
⇒(r)2 = (400 +2304) m2
⇒ r = 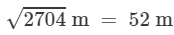
Question 15:
The radius of one circular field is 5 m and that of the other is 13 m. Find the radius of the circular field whose area is the difference of the areas of first and second field.
Answer 15:
Let the area of the circular field whose radius is 5 m be A1 , and the area of the circular field whose radius is 13 m be A2. Let A3 and r cm be the area and radius of the circular field, that is equal to the difference of the areas of the two fields.
∴ A3 = A2 -A1
A1 = π(5)2 = (25π) m2
A2 = π (13)2 = (169 π) m2
A3 = A2−A1 = (169π) −(25 π) = 144π m2
⇒A3 = π(r)2 = 144 π m2
⇒(r)2 = 144 m2
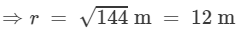
Hence, the radius of the circular field is 12 m.
Question 16:
Two circles are drawn inside a big circle with diameters 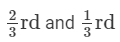 of the diameter of the big circle as shown in Fig. 18. Find the area of the shaded portion, if the length of the diameter of the circle is 18 cm.
of the diameter of the big circle as shown in Fig. 18. Find the area of the shaded portion, if the length of the diameter of the circle is 18 cm.
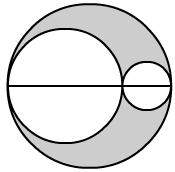
Answer 16:
Let the left circle be denoted as the 1st circle and the right circle be denoted as the 2nd circle.
Diameter of the big circle = 18 cm
Radius of the big circle = 9 cm
Diameter of the 1st circle =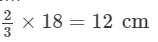
Radius of the 1st circle = 6 cm
Diameter of the 2nd circle = 
Radius of the 2nd circle = 3 cm
Area of the 1st circle = π(6)2=36π cm2
Area of the 2nd circle = π(3)2=π×3×3=9π cm2
Area of the big circle = π(9)2=π×9×9=81π cm2
Area of the shaded portion = Area of the big circle - (Area of the Ist circle + Area of the IInd circle)
Area of the shaded portion = 81π−(36π+9π)=36π cm2.
Question 17:
In Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
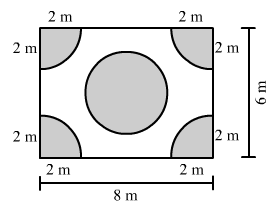
nswer 17:
Radius of the quarter circular plot = 2 m
Area of the quarter circular plot = 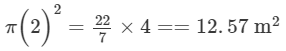
Radius of each flower bed = 2 m
Area of four flower beds = 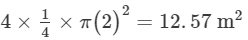
Area of the rectangular region = Length × Breadth
Area of the rectangular region = 8 × 6 = 48 m2
Area of the remaining field = Area of the rectangular region - (Area of the quarter circle + Area of the four flower beds)
Area of the remaining field = [48 - (12.57 + 12.57)] m2 = 22.86 m2
Question 18:
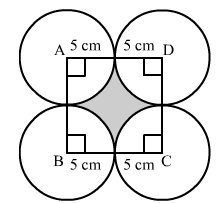
Four equal circles, each of radius 5 cm, touch each other as shown in Fig. 20. Find the area included between them. (Take π = 3.14).
Answer 18:
Side of the square = 10 cm
Area of the square = Side × Side
Area of the square = 10×10=100 cm2
Area of the four quarter circles = 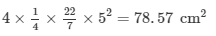
Area included in them = Area of the square - Area of the four quarter circles
Area included in them = ( 100 - 78.57 ) cm2 = 21.43 cm2 .
Question 19:
The area of circle is 100 times the area of another circle. What is the ratio of their circumferences?
Answer 19:
Let the area of the first circle be A1, the circumference be C1 and the radius be r1.
Let the area of the second circle be A2 , the circumference be C2 and the radius be r2.
Thus,
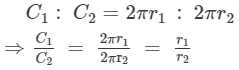
We know that :
A1 = 100A2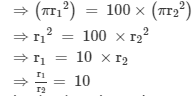
Substituting the values, we get:
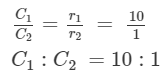
Hence, the ratio of their circumferences is 10:1.
FAQs on RD Sharma Solutions (Part - 2) - Ex-21.2, Mensuration - II Area of Circle, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the formula to calculate the area of a circle? |  |
| 2. How do I find the radius of a circle if I know its area? |  |
| 3. Can I use the diameter instead of the radius to calculate the area of a circle? |  |
| 4. What is the value of π? |  |
| 5. How can I use the formula for the area of a circle in real-life situations? |  |

|
Explore Courses for Class 7 exam
|

|

















