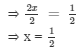RD Sharma Solutions (Part - 2) - Ex - 8.2, Linear Equations in One Variable, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 13:
Solve each of the following equations and check your answers:
3 (x + 2) = 15
Answer 13:
3 (x + 2) = 15
Dividing both sides by 3, we get
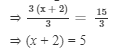
Subtracting 2 from both sides, we get
⇒ x + 2 −- 2 = 5 −- 2
⇒ x = 3
Verification:
Substituting x = 3 in LHS, we get
LHS = 3 (x + 2)= 3 (3+2) = 3××5 = 15, and RHS = 15
LHS = RHS
Hence, verified.
Question 14:
Solve each of the following equations and check your answers:
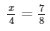
Answer 14:
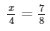
Multiplying both sides by 4, we get
Verification:
Substituting x = 7/2 in LHS, we get
LHS = 
LHS = RHS
Hence, verified.
Question 15:
Solve each of the following equations and check your answers:
Answer 15:
Subtracting 1/3 from both sides, we get
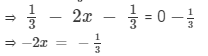
Multiplying both sides by −-1, we get
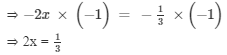
Dividing both sides by 2, we get
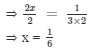
Verification:
Substituting x = 1/6 in LHS, we get
LHS = 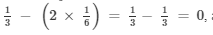
LHS = RHS
Hence, verified.
Question 16:
Solve each of the following equations and check your answers:
3(x + 6) = 24
Answer 16:
3(x + 6) = 24
Dividing both sides by 3, we get
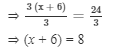
Subtracting 6 from both sides, we get
⇒ x + 6 − 6 = 8 − 6
⇒ x = 2
Verification:
Substituting x = 2 in LHS, we get
LHS = 3 (x + 6) = 3 (2 + 6) = 3×8 = 24, and RHS = 24
LHS = RHS
Hence, verified.
Question 17:
Solve each of the following equations and check your answers:
3(x + 2) − 2(x − 1) = 7
Answer 17:
3(x + 2) − 2(x − 1) = 7
On expanding the brackets, we get
⇒ (3× x) +( 3 × 2) − (2 × x) + (2 × 1) = 73× x + 3 × 2 - 2 × x + 2 × 1 = 7
⇒ 3x + 6 − 2x + 2 = 7
⇒ 3x − 2x + 6 + 2 = 7
⇒ x + 8 = 7
Subtracting 8 from both sides, we get
⇒ x + 8 − 8 = 7 − 8
⇒ x = −1
Verification:
Substituting x = −1 in LHS, we get
LHS = 3 (x + 2) −2(x −1), and RHS = 7
LHS = 3 (−1 + 2) −2(−1−1) = (3×1) − (2×−2) = 3 + 4 = 7, and RHS = 7
LHS = RHS
Hence, verified.
Question 18:
Solve each of the following equations and check your answers:
8(2x − 5) − 6(3x − 7) = 1
Answer 18:
8(2x − 5) − 6(3x − 7) = 1
On expanding the brackets, we get
⇒ (8×2x) − (8 × 5) − (6 × 3x) + (−6)×(−7) = 1
⇒ 16x − 40 − 18x + 42 = 1
⇒ 16x − 18x + 42 − 40 = 1
⇒ −2x + 2 = 1
Subtracting 2 from both sides, we get
⇒ −2x + 2 −2 = 1 − 2
⇒ −2x = −1
Multiplying both sides by −1, we get
⇒ −2x ×(−1) = −1×(−1)
⇒ 2x = 1
Dividing both sides by 2, we get
Verification:
Substituting x = 1/2 in LHS, we get
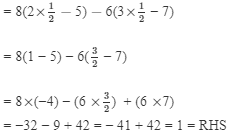
LHS = RHS
Hence, verified
Question 19:
Solve each of the following equations and check your answers:
6(1 − 4x) + 7(2 + 5x) = 53
Answer 19:
6(1 − 4x) + 7(2 + 5x) = 53
On expanding the brackets, we get
⇒ (6×1) − (6 × 4x) + (7 ×2) + (7×5x) = 53
⇒ 6 −24x + 14 + 35x = 53
⇒ 6 + 14 + 35x −24x = 53
⇒ 20 + 11x = 53
Subtracting 20 from both sides, we get
⇒ 20 + 11x −20 = 53 −- 20
⇒ 11x = 33
⇒ Dividing both sides by 11, we get
11x/11 = 33/11
⇒ x = 3
Verification:
Substituting x = 3 in LHS, we get
= 6(1 − 4××3) + 7(2 + 5××3)
= 6(1 − 12) + 7(2 + 15)
= 6(−11) + 7(17)
= −66 + 119 = 53 = RHS
LHS = RHS
Hence, verified.
Question 20:
Solve each of the following equations and check your answers:
5(2 − 3x) − 17(2x − 5) = 16
Answer 20:
5(2 − 3x) − 17(2x − 5) = 16
On expanding the brackets, we get
⇒ (5××2) −- (5 ×× 3x) − (17 ××2x ) + (17××5) = 16
⇒ 10 −- 15x − 34x + 85 = 16
⇒ 10 + 85 − 34x −- 15x = 16
⇒ 95 - 49x = 16
Subtracting 95 from both sides, we get
⇒ - 49x + 95 −- 95 = 16 −- 95
⇒ - 49x = -79
Dividing both sides by -49, we get
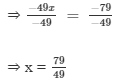
Verification:
Substituting x = 79/49 in LHS, we get
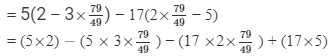
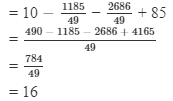
= RHS
So, LHS = RHS
Hence, verified.
Question 21:
Solve each of the following equations and check your answers:
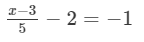
Answer 21:
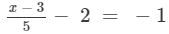
Adding 2 to both sides, we get
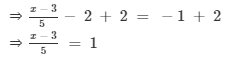
Multiplying both sides by 5, we get
Adding 3 to both sides, we get
⇒ x −3 + 3 = 5 + 3
⇒ x = 8
Verification:
Substituting x = 8 in LHS, we get
= RHS
LHS = RHS
Hence, verified.
Question 22:
Solve each of the following equations and check your answers:
5(x − 2) + 3(x + 1) = 25
Answer 22:
5(x − 2) + 3(x + 1) = 25
On expanding the brackets, we get
⇒ (5 ×× x) −- (5 ×× 2) + (3 ×× x) + (3××1) = 25
⇒ 5x −- 10 + 3x + 3 = 25
⇒ 5x + 3x −- 10 + 3 = 25
⇒ 8x −- 7 = 25
Adding 7 to both sides, we get
⇒ 8x −- 7 + 7 = 25 +7
⇒ 8x = 32
Dividing both sides by 8, we get
Verification:
Substituting x = 4 in LHS, we get
= 5(4 − 2) + 3(4 + 1)
= 5(2) + 3(5)
= 10 + 15
= 25
= RHS
LHS = RHS
Hence, verified.
FAQs on RD Sharma Solutions (Part - 2) - Ex - 8.2, Linear Equations in One Variable, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are linear equations in one variable? |  |
| 2. How can I solve linear equations in one variable? |  |
| 3. Can linear equations in one variable have multiple solutions? |  |
| 4. Are there any real-life applications of linear equations in one variable? |  |
| 5. Are there any tips or tricks to solve linear equations in one variable more efficiently? |  |