RD Sharma Solutions (Part - 3) - Ex-20.1, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
QUESTION 16:
A lane 180 m long and 5 m wide is to be paved with bricks of length 20 cm and breadth 15 cm. Find the cost of bricks that are required, at the rate of Rs 750 per thousand.
ANSWER 16:
We have,
Length of the lane = 180 m
Breadth of the lane = 5 m
Area of a lane = Length x Breadth = 180 m x 5 m = 900 m2
Length of the brick = 20 cm
Breadth of the brick = 15 cm
Area of a brick = Length x Breadth = 20 cm x 15 cm = 300 cm2 = 0.03 m2 [Since 1 m2 = 10000 cm2 ]
Required number of bricks = 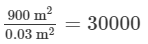
Cost of 1000 bricks = Rs. 750
∴ Total cost of 30,000 bricks = Rs. 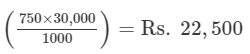
QUESTION 17:
How many envelopes can be made out of a sheet of paper 125 cm by 85 cm; supposing one envelope requires a piece of paper of size 17 cm by 5 cm?
ANSWER 17:
We have,
Length of the sheet of paper = 125 cm
Breadth of the sheet of paper = 85 cm
Area of a sheet of paper = Length x Breadth = 125 cm x 85 cm = 10,625 cm2
Length of sheet required for an envelope = 17 cm
Breadth of sheet required for an envelope = 5 cm
Area of the sheet required for one envelope = Length x Breadth = 17 cm x 5 cm = 85 cm2
Thus,
Required number of envelopes = 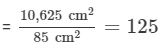
QUESTION 18:
The width of a cloth is 170 cm. Calculate the length of the cloth required to make 25 diapers, if each diaper requires a piece of cloth of size 50 cm by 17 cm.
ANSWER 18:
We have,
Length of the diaper = 50 cm
Breadth of the diaper = 17 cm
Area of cloth to make 1 diaper = Length x Breadth = 50 cm x 17 cm = 850 cm2
Thus,
Area of 25 such diapers = (25 x 850) cm2 = 21,250 cm2
Area of total cloth = Area of 25 diapers
= 21,250 cm2
It is given that width of a cloth = 170 cm
∴ Length of the cloth = 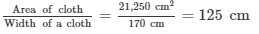
Hence, length of the cloth will be 125 cm.
QUESTION 19:
The carpet for a room 6.6 m by 5.6 m costs Rs 3960 and it was made from a roll 70 cm wide. Find the cost of the carpet per metro.
ANSWER 19:
We have,
Length of a room = 6.6 m
Breadth of a room = 5.6 m
Area of a room = Length x Breadth = 6.6 m x 5.6 m = 36.96 m2
Width of a carpet = 70 cm = 0.7 m [Since 1 m = 100 cm]
Length of a carpet = 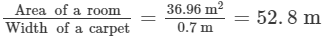
Cost of 52.8 m long roll of carpet = Rs. 3960
Therefore,
Cost of 1 m long roll of carpet = Rs. 3960/52.8= Rs. 75
QUESTION 20:
A room is 9 m long, 8 m broad and 6.5 m high. It has one door of dimensions 2 m × 1.5 m and three windows each of dimensions 1.5 m × 1 m. Find the cost of white washing the walls at Rs 3.80 per square metre.
ANSWER 20:
We have,
Length of a room = 9 m
Breadth of a room = 8 m
Height of a room = 6.5 m
Area of 4 walls = 2(l + b)h
= 2(9 m + 8 m) x 6.5 m = 2 x 17 m x 6.5 m = 221 m2
Length of a door = 2 m
Breadth of a door = 1.5 m
Area of a door = Length x Breadth = 2 m x 1.5 m = 3 m2
Length of a window = 1.5 m
Breadth of a window = 1 m
Since, area of one window = Length x Breadth = 1.5 m x 1 m = 1.5 m2
Thus,
Area of 3 such windows = 3 x 1.5 m2 = 4.5 m2
Area to be white-washed = Area of 4 walls − (Area of one door + Area of 3 windows)
Area to be white-washed = [221 − (3 + 4.5 )] m2
= (221 − 7.5 ) m2 = 213.5 m2
Cost of white-washing for 1 m2 area = Rs. 3.80
∴ Cost of white-washing for 213.5 m2 area = Rs. (213.5 x 3.80) = Rs. 811.30
QUESTION 21:
A hall 36 m long and 24 m broad allowing 80 m2 for doors and windows, the cost of papering the walls at Rs 8.40 per m2 is Rs 9408. Find the height of the hall.
ANSWER 21:
We have,
Length of the hall = 36 m
Breadth of the hall = 24 m
Let h be the height of the hall.
Now, in papering the wall, we need to paper the four walls excluding the floor and roof of the hall.
So, the area of the wall which is to be papered = Area of 4 walls
= 2h(l + b)
= 2h (36 + 24) = 120h m2
Now, area left for the door and the windows = 80 m2
So, the area which is actually papered = (120h − 80) m2
Again,
The cost of papering the walls at Rs 8.40 per m2 = Rs. 9408.
⇒ (120h − 80) m2 x Rs. 8.40 per m2 = Rs. 9408
⇒ (120h − 80) m2 = 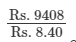
⇒ (120h − 80) m2 = 1120 m2
⇒ 120h m2 = (1120 + 80) m2
⇒ 120h m2 = 1200 m2

Hence, the height of the wall would be 10 m.
FAQs on RD Sharma Solutions (Part - 3) - Ex-20.1, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the different types of mensuration? |  |
| 2. How do you calculate the area of a rectangle? |  |
| 3. What is the formula for finding the volume of a cube? |  |
| 4. How do you find the surface area of a cylinder? |  |
| 5. How can I calculate the volume of a sphere? |  |
















