17.2, Constructions, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
QUESTION 1:
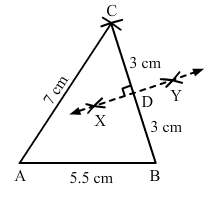
Draw ∆ ABC in which AB = 5.5 cm, BC = 6 cm and CA = 7 cm. Also, draw perpendicular bisector of side BC.
ANSWER 1:
Steps of construction:
- Draw a line segment AB of length 5.5 cm.
- From B, cut an arc of radius 6 cm.
- With centre A, draw an arc of radius 7 cm intersecting the previously drawn arc at say, C.
- Join AC and BC to obtain the desired triangle.
- With centre B and radius more than 1/2BC, draw two arcs on both sides of BC.
- With centre C and the same radius as in the previous step, draw two arcs intersecting the arcs drawn in the previous step at X and Y.
- Join XY to get the perpendicular bisector of BC.
QUESTION 2:
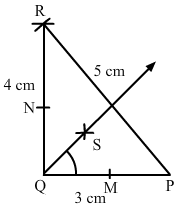
Draw ∆ PQR in which PQ = 3 cm, QR = 4 cm and RP = 5 cm. Also, draw the bisector of ∠Q.
ANSWER 2:
Steps of construction:
- Draw a line segment PQ of length 3 cm.
- With Q as centre and radius 4 cm, draw an arc.
- With P as centre and radius 5 cm, draw an arc intersecting the previously drawn arc at R.
- Join PR and QR to obtain the required triangle.
- From Q, cut arcs of equal radius intersecting PQ and QR at M and N, respectively.
- From M and N, cut arcs of equal radius intersecting at point S.
- Join QS and extend to produce the angle bisector of angle PQR.
- Verify that angle PQS and angle SQR are equal to 45° each.
QUESTION 3:
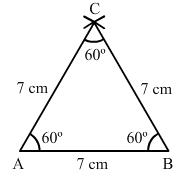
Draw an equilateral triangle one of whose sides is of length 7 cm.
ANSWER 3:
Steps of construction:
- Draw a line segment AB of length 7 cm.
- With centre A, draw an arc of radius 7 cm.
- With centre B, draw an arc of radius 7 cm intersecting the previously drawn arc at C.
- Join AC and BC to get the required triangle.
QUESTION 4:
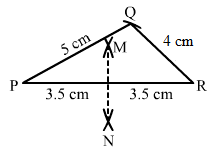
Draw a triangle whose sides are of lengths 4 cm, 5 cm and 7 cm. Draw the perpendicular bisector of the largest side.
ANSWER 4:
Steps of construction:
- Draw a line segment PR of length 7 cm.
- With centre P, draw an arc of radius 5 cm.
- With centre R, draw an arc of radius 4 cm intersecting the previously drawn arc at Q.
- Join PQ and QR to obtain the required triangle.
- From P, draw arcs with radius more than half of PR on either sides.
- With the same radius as in the previous step, draw arcs from R on either sides of PR intersecting the arcs drawn in the previous step at M and N.
- MN is the required perpendicular bisector of the largest side.
QUESTION 5:
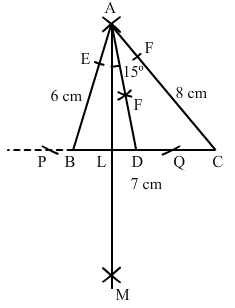
Draw a triangle ABC with AB = 6 cm, BC = 7 cm and CA = 8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
ANSWER 5:
Steps of construction:
- Draw a line segment BC of length 7 cm.
- With centre B, draw an arc of radius 6 cm.
- With centre C, draw an arc of radius 8 cm intersecting the previously drawn arc at A.
- Join AC and BC to get the required triangle.
Angle bisector steps:
1. From A, cut arcs of equal radius intersecting AB and AC at E and F, respectively.
2. From E and F, cut arcs of equal radius intersecting at point H.
3. Join AH and extend to produce the angle bisector of angle A, meeting line BC at D.
Perpendicular from Point A to line BC steps:
1. From A, cut arcs of equal radius intersecting BC at P and Q, respectively (Extend BC to draw these arcs).
2. From P and Q, cut arcs of equal radius intersecting at M.
3. Join AM cutting BC at L.
4. AL is the perpendicular to the line BC.
5. Angle LAD is 15o.
QUESTION 6:
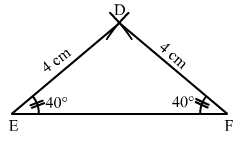
Draw ∆ DEF such that DE = DF = 4 cm and EF = 6 cm. Measure ∠E and ∠F.
ANSWER 6:
Steps of construction:
- Draw a line segment EF of length 6 cm.
- With E as centre, draw an arc of radius 4 cm.
- With F as centre, draw an arc of radius 4 cm intersecting the previous arc at D.
- Join DE and DF to get the desired triangle.DF, .
By measuring we get,∠E=∠F=40°∠E=∠F=40°
QUESTION 7:
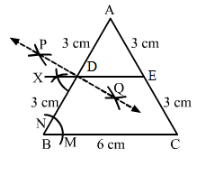
Draw any triangle ABC. Bisect side AB at D. Through D, draw a line parallel to BC, meeting AC in E. Measure AE and EC.
ANSWER 7:
We first draw a triangle ABC with each side = 6 cm.
Steps to bisect line AB:
1. Draw an arc from A on either side of line AB.
2. With the same radius as in the previous step, draw an arc from B on either side of AB intersecting the arcs drawn in the previous step at P and Q.
3. Join PQ cutting AB at D. PQ is the perpendicular bisector of AB.
Parallel line to BC:
1. With B as centre, draw an arc cutting BC and BA at M and N, respectively.
2. With centre D and the same radius as in the previous step, draw an arc on the opposite side of AB to cut AB at Y.
3. With centre Y and radius equal to MN, draw an arc cutting the arc drawn in the previous step at X.
4. Join XD and extend it to intersect AC at E.
5. DE is the required parallel line.
FAQs on 17.2, Constructions, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are RD Sharma Solutions? |  |
| 2. What is the significance of Class 7 RD Sharma Solutions? |  |
| 3. How can RD Sharma Solutions benefit Class 7 students? |  |
| 4. Are RD Sharma Solutions available online? |  |
| 5. Can RD Sharma Solutions help in exam preparation? |  |
















