Class 7 Exam > Class 7 Notes > RD Sharma Solutions for Class 7 Mathematics > RD Sharma Solutions - 17.4, Constructions, Class 7, Math
17.4, Constructions, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
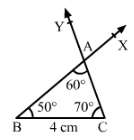
Question 1:
Construct ∆ ABC in which BC = 4 cm, ∠B = 50° and ∠C = 70°.
Answer 1:
Steps of construction:
- Draw a line segment BC of length 4 cm.
- Draw ∠CBX such that ∠CBX=50°.
- Draw ∠BCY with Y on the same side of BC as X such that ∠BCY = 70°°.
- Let CY and BX intersect at A.
- ABC is the required triangle.
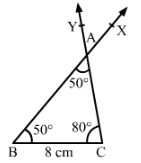
Question 2:
Draw ∆ ABC in which BC = 8 cm, ∠B = 50° and ∠A = 50°.
Answer 2:
∠ABC+∠BCA+∠CAB=180°
∠BCA=180°−∠ABC−∠CAB
∠BCA=180°−100°=80°
Steps of construction:
- Draw a line segment BC of length 8 cm.
- Draw ∠CBX such that ∠CBX = 50°.
- Draw ∠BCY with Y on the same side of BC as X such that ∠BCY = 80°°.
- Let CY and BX intersect at A.
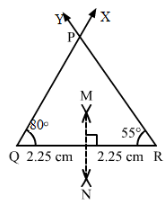
Question 3:
Draw ∆ PQR in which ∠Q = 80°, ∠R = 55° and QR = 4.5 cm. Draw the perpendicular bisector of side QR.
Answer 3:
Steps of construction:
- Draw a line segment QR = 4.5 cm.
- Draw ∠RQX = 80° and ∠QRY =55°.
- Let QX and RY intersect at P so that PQR is the required triangle.
- With Q as centre and radius more that 2.25 cm, draw arcs on either sides of QR.
- With R as centre and radius more than 2.25 cm, draw arcs intersecting the previous arcs at M and N.
- Join MN; MN is the required perpendicular bisector of QR.
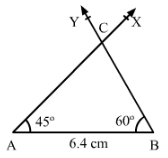
Question 4:
Construct ∆ ABC in which AB = 6.4 cm, ∠A = 45° and ∠B = 60°.
Answer 4:
Steps of construction:
- Draw a line segment AB = 6.4 cm.
- Draw ∠BAX = 45°∠BAX = 45°.
- Draw ∠ABY with Y on the same side of AB as X such that ∠ABY = 60°°.
Let AX and BY intersect at C; ABC is the required triangle.
Question 5:
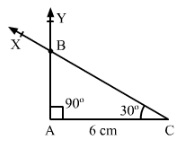
Draw ∆ ABC in which AC = 6 cm, ∠A = 90° and ∠B = 60°.
Answer 5:
We can see that ∠A+∠B+∠C = 180°. Therefore ∠C = 180°° − 60°° − 90°° = 30°.
Steps of construction:
- Draw a line segment AC = 6 cm.
- Draw ∠ACX=30°.
- Draw ∠CAY with Y on the same side of AC as X such that ∠CAY = 90°°.
- Join CX and AY. Let these intersect at B.
- ABC is the required triangle where angle ∠ABC = 60°
The document 17.4, Constructions, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics is a part of the Class 7 Course RD Sharma Solutions for Class 7 Mathematics.
All you need of Class 7 at this link: Class 7
FAQs on 17.4, Constructions, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are RD Sharma Solutions? |  |
Ans. RD Sharma Solutions are comprehensive solutions provided for the RD Sharma textbook, which is widely used for mathematics in the CBSE curriculum. These solutions are designed to help students understand and solve the mathematical problems in a step-by-step manner.
| 2. Which class and chapter does RD Sharma Solutions - 17.4, Constructions, Class 7, Math Class 7 cover? |  |
Ans. RD Sharma Solutions - 17.4, Constructions, Class 7, Math Class 7 covers the topic of Constructions in mathematics for Class 7 students.
| 3. What is the purpose of the chapter on constructions in mathematics? |  |
Ans. The chapter on constructions in mathematics teaches students how to construct various geometric shapes and figures using a compass, ruler, and other tools. It helps students develop their spatial visualization skills and understand the principles of construction.
| 4. Are RD Sharma Solutions helpful for exam preparation? |  |
Ans. Yes, RD Sharma Solutions are highly beneficial for exam preparation. These solutions provide detailed explanations and step-by-step solutions for the textbook problems, helping students understand the concepts thoroughly. By practicing with these solutions, students can improve their problem-solving skills and enhance their chances of performing well in exams.
| 5. Where can I find RD Sharma Solutions for Class 7, Math Class 7? |  |
Ans. RD Sharma Solutions for Class 7, Math Class 7 can be found in various formats. They are available in the RD Sharma textbook itself, or you can also find them online on educational websites, forums, or through mobile applications specifically designed for providing RD Sharma Solutions.
Related Searches





















