Chapter 14 - Compound Interest (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 14.4:
Question 1:
Find the compound interest when principal = Rs 3000, rate = 5% per annum and time = 2 years.
ANSWER:
Principal for the first year = Rs 3,000
Interest for the first year = Rs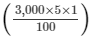
= Rs 150
Amount at the end of the first year = Rs 3,000 + Rs 150
= Rs 3,150
Principal for the second year = Rs 3,150
Interest for the second year = Rs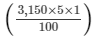
= Rs 157.50
Amount at the end of the second year = Rs 3,150 + Rs 157.50
= Rs 3307.50
∴ Compound interest = Rs(3,307.50 − 3,000)
= Rs 307.50
PAGE NO 14.4:
Question 2:
What will be the compound interest on Rs 4000 in two years when rate of interest is 5% per annum?
ANSWER:
We know that amount A at the end of n years at the rate of R% per annum is given by A = P(1 + R/100)n.
Given:P = Rs 4,000
R = 5% p.a.
n = 2 years
Now,A = 4,000(1 + 5/100)²
= 4,000(1.05)²
= Rs 4,410
And,CI = A − P
= Rs 4,410 − Rs 4,000
= Rs 410
PAGE NO 14.4:
Question 3:
Rohit deposited Rs 8000 with a finance company for 3 years at an interest of 15% per annum. What is the compound interest that Rohit gets after 3 years?
ANSWER:
We know that amount A at the end of n years at the rate of R% per annum is given by A = P(1 + R/100)n.
Given:P = Rs 8,000
R = 15% p.a.
n = 3 years
Now,A = 8,000(1 + 15/100)³
= 8,000(1.15)³
= Rs 12,167
And,CI = A − P
= Rs 12,167 − Rs 8,000
= Rs 4,167
PAGE NO 14.4:
Question 4:
Find the compound interest on Rs 1000 at the rate of 8% per annum for 1.5 years when interest is compounded half-yearly.
ANSWER:
Given:P = Rs 1,000
R = 8% p.a.
n = 1.5 years
We know that:A = P(1 + R/200)²n
= 1,000(1 + 8/200)³
= 1,000(1.04)³
= Rs 1,124.86
Now,CI = A − P
= Rs 1,124.86 − Rs 1,000
= Rs 124.86
PAGE NO 14.4:
Question 5:
Find the compound interest on Rs 160000 for one year at the rate of 20% per annum, if the interest is compounded quarterly.
ANSWER:
Given:P = Rs 16,000
R = 20% p.a.
n = 1 year
We know that:A = P(1 + R/400)4n
= 16,000(1 + 20/400)4
= 16,000(1.05)4
= Rs 19,448.1
Now,CI = A − P
= Rs 19,448.1 − Rs 16,000
= Rs 3,448.1
PAGE NO 14.5:
Question 6:
Swati took a loan of Rs 16000 against her insurance policy at the rate of 12.5% per annum. Calculate the total compound interest payable by Swati after 3 years.
ANSWER:
Given:P = Rs 16,000
R = 12.5% p.a.
n = 3 years
We know that:A = P(1 + R/100)n
= 16,000(1 + 12.5/100)³
= 16,000(1.125)³ = Rs 22,781.25
Now, CI = A − P
= Rs 22,781.25 − Rs 16,000
= Rs 6,781.25
PAGE NO 14.5:
Question 7:
Roma borrowed Rs 64000 from a bank for 1.5 years at the rate of 10% per annum. Compute the total compound interest payable by Roma after 1.5 years, if the interest is compounded half-yearly.
ANSWER:
Given:P = Rs 64,000
R = 10% p.a.
n = 1.5 years
Amount after n years:
A = P(1 + R/200)²n
= 64,000(1 + 10/200)³
= 64,000(1.05)³
= Rs 74,088
Now,CI = A − P
= Rs 74,088 − Rs 64,000
= Rs 10,088
PAGE NO 14.5:
Question 8:
Mewa Lal borrowed Rs 20000 from his friend Rooplal at 18% per annum simple interest. He lent it to Rampal at the same rate but compounded annually. Find his gain after 2 years.
ANSWER:
SI for Mewa Lal = PRT/100
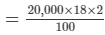
= Rs 7,200
Thus, he has to pay Rs 7,200 as interest after borrowing.
CI for Mewa Lal = A − P
= 20,000(1 + 18/100)² − 20,000
= 20,000(1.18)² − 20,000
= 27,848 − 20,000
= Rs 7,848
He gained Rs 7,848 as interest after lending.
His gain in the whole transaction = Rs 7,848 − Rs 7,200
= Rs 648
PAGE NO 14.5:
Question 9:
Find the compound interest on Rs 8000 for 9 months at 20% per annum compounded quarterly.
ANSWER:
P = Rs 8,000
T = 9 months = 3 quarters
R = 20% per annum = 5% per quarter
A = 8,000(1 + 5/100)³
= 8,000(1.05)³
= 9,261
The required amount is Rs 9,261.
Now,CI = A − P
= Rs 9,261 − Rs 8,000
= Rs 1,261
PAGE NO 14.5:
Question 10:
Find the compound interest at the rate of 10% per annum for two years on that principal which in two years at the rate of 10% per annum gives Rs 200 as simple interest.
ANSWER:
SI = PRT100
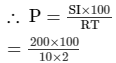
Rs 1,000
A = P(1 + R/100)n
= 1,000(1 + 10/100)²
= 1,000(1.10)² = Rs 1,210
Now,CI = A − P
= Rs 1,210 − Rs 1,000
= Rs 210
PAGE NO 14.5:
Question 11:
Find the compound interest on Rs 64000 for 1 year at the rate of 10% per annum compounded quarterly.
ANSWER:
To calculate the interest compounded quarterly, we have:
A = P(1 + R/400)4n
= 64,000(1 + 10/400)4×1
= 64,000(1.025)4
= 70,644.03
Thus, the required amount is Rs 70,644.03.
Now,CI = A − P
= Rs 70,644.025 − Rs 64,000
= Rs 6,644.03
PAGE NO 14.5:
Question 12:
Ramesh deposited Rs 7500 in a bank which pays him 12% interest per annum compounded quarterly. What is the amount which he receives after 9 months.
ANSWER:
Given:P = Rs 7,500
R = 12% p.a. = 3% quarterly
T = 9 months = 3 quarters
We know that:A = P(1 + R/100)n
A = 7,500(1 + 3/100)³
= 7,500(1.03)³ = 8,195.45
Thus, the required amount is Rs 8,195.45.
PAGE NO 14.5:
Question 13:
Anil borrowed a sum of Rs 9600 to install a handpump in his dairy. If the rate of interest is 5.5% per annum compounded annually, determine the compound interest which Anil will have to pay after 3 years.
ANSWER:
A = P(1 + R/100)n
= 9,600(1 + 5.5/100)³
= 9,600(1.055)³ = Rs 11,272.72
Now,CI = A − P
= Rs 11,272.72 − Rs 9,600
= Rs 1,672.72
PAGE NO 14.5:
Question 14:
Surabhi borrowed a sum of Rs 12000 from a finance company to purchase a refrigerator. If the rate of interest is 5% per annum compounded annually, calculate the compound interest that Surabhi has to pay to the company after 3 years.
ANSWER:
A = P(1 + R/100)n
= 12,000(1 + 5/100)³
= 12,000(1.05)³ = 13,891.50
Thus, the required amount is Rs 13,891.50.
Now,CI = A − P
= Rs 13,891.50 − Rs 12,000
= Rs 1,891.50
PAGE NO 14.5:
Question 15:
Daljit received a sum of Rs. 40000 as a loan from a finance company. If the rate of interest is 7% per annum compounded annually, calculate the compound interest that Daljit pays after 2 years.
ANSWER:
A = P(1 + R/100)n
= 40,000(1 + 7/100)²
= 40,000(1.07)²
= 45,796
Thus, the required amount is Rs 45,796.
Now,CI = A − P
= Rs 45,796 − Rs 40,000
= Rs 5,796
FAQs on Chapter 14 - Compound Interest (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is compound interest and how is it different from simple interest? |  |
| 2. How is compound interest calculated? |  |
| 3. Can you provide an example to understand compound interest better? |  |
| 4. How does the frequency of compounding affect compound interest? |  |
| 5. Is compound interest always beneficial? |  |





















