RD Sharma Solutions Ex-1.4, Number System, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Define an irrational number.
Solution: An irrational number is a real number which can be written as a decimal but not as a fraction i.e. it cannot be expressed as a ratio of integers. It cannot be expressed as terminating or repeating decimal.
Q2. Explain how an irrational number is differing from rational numbers?
Solution: An irrational number is a real number which can be written as a decimal but not as a fraction i.e. it cannot be expressed as a ratio of integers. It cannot be expressed as terminating or repeating decimal.
For example, 0.10110100 is an irrational number
A rational number is a real number which can be written as a fraction and as a decimal i.e. it can be expressed as a ratio of integers. . It can be expressed as terminating or repeating decimal.
For examples,
0.10 and 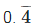 both are rational numbers
both are rational numbers
Q3. Find, whether the following numbers are rational and irrational
(i) √7
(ii) √4
(iii) 2+√3
(iv) √3+√2
(v) √3+5
(vi) (√2 − 2)2
(vii) (2−√2)(2+√2)
(viii) (√2+√3)2
(ix) √5 – 2
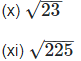
(xii) 0.3796
(xiii) 7.478478……
(xiv) 1.101001000100001……
Solution:
(i) √7is not a perfect square root so it is an Irrational number.
(ii) √4 is a perfect square root so it is an rational number.
We have,
√4 can be expressed in the form of
ab, so it is a rational number. The decimal
representation of √9 is 3.0. 3 is a rational number.
(iii) 2+√3
Here, 2 is a rational number and √3 is an irrational number
So, the sum of a rational and an irrational number is an irrational number.
(iv) √3+√2
√3 is not a perfect square and it is an irrational number and √2 is not a perfect square and is an irrational number. The sum of an irrational number and an irrational number is an irrational number, so √3+√2 is an irrational number.
(v) √3+√5
√3 is not a perfect square and it is an irrational number and √5 is not a perfect square and is an irrational number. The sum of an irrational number and an irrational number is an irrational number, so √3+√5 is an irrational number.
(vi) (√2−2)2
We have, (√2−2)2
= 2 + 4 - 4 √2
= 6 + 4 √2
6 is a rational number but 4√2 is an irrational number.
The sum of a rational number and an irrational number is an irrational number, so (√2+√4)2 is an irrational number.

We have,
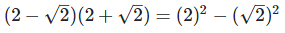 [Since, (a + b)(a - b) = a2 – b2]
[Since, (a + b)(a - b) = a2 – b2]
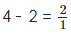
Since, 2 is a rational number.
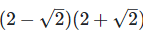 is a rational number.
is a rational number.
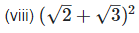
We have,
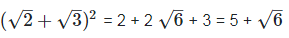 [Since, (a+b)2 = a2 + 2ab + b2
[Since, (a+b)2 = a2 + 2ab + b2
The sum of a rational number and an irrational number is an irrational number, so 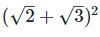 is an irrational number.
is an irrational number.
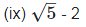
The difference of an irrational number and a rational number is an irrational number.
(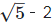 ) is an irrational number.
) is an irrational number.
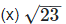
 = 4.795831352331…
= 4.795831352331…
As decimal expansion of this number is non-terminating, non-recurring so it is an irrational number.
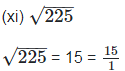
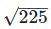 is rational number as it can be represented in p/q form.
is rational number as it can be represented in p/q form.
(xii) 0.3796
0.3796, as decimal expansion of this number is terminating, so it is a rational number.
(xiii) 7.478478……
7.478478 = 7.478, as decimal expansion of this number is non-terminating recurring so it is a rational number.
(xiv) 1.101001000100001……
1.101001000100001……, as decimal expansion of this number is non-terminating, non-recurring so it is an irrational number
Q4. Identify the following as irrational numbers. Give the decimal representation of rational numbers:
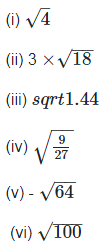
Solution:
(i) We have,
√4 can be written in the form of
p/q. So, it is a rational number. Its decimal
representation is 2.0
(ii). We have,

Since, the product of a ratios and an irrational is an irrational number.
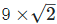 is an irrational.
is an irrational.
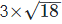 is an irrational number.
is an irrational number.
(iii) We have,
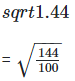
= 12/10
= 1.2
Every terminating decimal is a rational number, so 1.2 is a rational number.
Its decimal representation is 1.2.
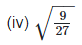
We have,
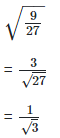
Quotient of a rational and an irrational number is irrational numbers so
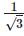 is an irrational number.
is an irrational number.
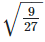 is an irrational number.
is an irrational number.
(v) We have,
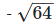
= - 8
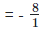 can be expressed in the form of a/b,
can be expressed in the form of a/b,
so 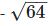
is a rational number.
Its decimal representation is - 8.0.
(vi) We have,

= 10 can be expressed in the form of a/b,
so 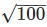 is a rational number
is a rational number
Its decimal representation is 10.0.
Q5. In the following equations, find which variables x, y and z etc. represent rational or irrational numbers:
(i) x2 = 5
(ii) y2 = 9
(iii) z2 = 0.04
(iv) u2 = 17/4
(v) v2 = 3
(vi) w2 = 27
(vii) t2 = 0.4
Solution:
(i) We have,
x2 = 5
Taking square root on both the sides, we get
x = √5
√5 is not a perfect square root, so it is an irrational number.
(ii) We have,
= y2 = 9
= 3
= 3/1 can be expressed in the form of a/b, so it a rational number.
(iii) We have,
z2 = 0.04
Taking square root on the both sides, we get
z = 0.2
2/10 can be expressed in the form of a/b, so it is a rational number.
(iv) We have,
u2 = 17/4
Taking square root on both sides, we get,
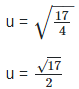
Quotient of an irrational and a rational number is irrational, so u is an Irrational number.
(v) We have,
v2 = 3
Taking square root on both sides, we get,
v = √3
√3 is not a perfect square root, so v is irrational number.
(vi) We have,
w2 = 27
Taking square root on both the sides, we get,
w = 3√3
Product of a irrational and an irrational is an irrational number. So w is an irrational number.
(vii) We have,
t2 = 0. 4
Taking square root on both sides, we get,
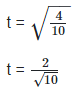
Since, quotient of a rational and an Irrational number is irrational number. t2 = 0.4 is an irrational number.
Q6. Give an example of each, of two irrational numbers whose:
(i) Difference in a rational number.
(ii) Difference in an irrational number.
(iii) Sum in a rational number.
(iv) Sum is an irrational number.
(v) Product in a rational number.
(vi) Product in an irrational number.
(vii) Quotient in a rational number.
(viii) Quotient in an irrational number.
Solution:  is an irrational number.
is an irrational number.
Now, 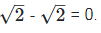
0 is the rational number.
(ii) Let two irrational numbers are 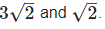
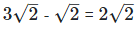
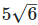 is the rational number.
is the rational number.
(iii) 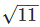 is an irrational number.
is an irrational number.
Now, 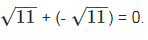
0 is the rational number.
(iv) Let two irrational numbers are 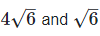
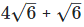
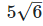 is the rational number.
is the rational number.
(iv) Let two Irrational numbers are  and √ 5
and √ 5
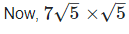
= 7 × 5
= 35 is the rational number.
(v) Let two irrational numbers are 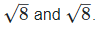
Now, 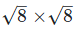
8 is the rational number.
(vi) Let two irrational numbers are 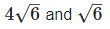
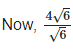
= 4 is the rational number
(vii) Let two irrational numbers are 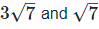
Now, 3 is the rational number.
(viii) Let two irrational numbers are 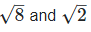
Now 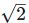 is an rational number.
is an rational number.
Q7. Give two rational numbers lying between 0.232332333233332 and 0.212112111211112.
Solution: Let a = 0.212112111211112
And, b = 0.232332333233332...
Clearly, a < b because in the second decimal place a has digit 1 and b has digit 3 If we consider rational numbers in which the second decimal place has the digit 2, then they will lie between a and b.
Let. x = 0.22
y = 0.22112211... Then a < x < y < b
Hence, x, and y are required rational numbers.
Q8. Give two rational numbers lying between 0.515115111511115 and 0. 5353353335
Solution: Let, a = 0.515115111511115...
And, b = 0.5353353335..
We observe that in the second decimal place a has digit 1 and b has digit 3, therefore, a < b.
So If we consider rational numbers
x = 0.52
y = 0.52062062...
We find that,
a < x < y < b
Hence x and y are required rational numbers.
Q9. Find one irrational number between 0.2101 and 0.2222 ... 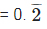
Solution: Let, a = 0.2101 and,
b =0.2222...
We observe that in the second decimal place a has digit 1 and b has digit 2, therefore a < b in the third decimal place a has digit 0.
So, if we consider irrational numbers
x = 0.211011001100011....
We find that a < x < b
Hence x is required irrational number.
Q10. Find a rational number and also an irrational number lying between the numbers 0.3030030003... and 0.3010010001...
Solution: Let,
a = 0.3010010001 and,
b = 0.3030030003...
We observe that in the third decimal place a has digit 1 and b has digit
3, therefore a < b in the third decimal place a has digit 1. So, if we
consider rational and irrational numbers
x = 0.302
y = 0.302002000200002.....
We find that a < x < b and, a < y < b.
Hence, x and y are required rational and irrational numbers respectively.
Q11. Find two irrational numbers between 0.5 and 0.55.
Solution: Let a = 0.5 = 0.50 and b =0.55
We observe that in the second decimal place a has digit 0 and b has digit
5, therefore a < 0 so, if we consider irrational numbers
x =0.51051005100051...
y = 0.530535305353530...
We find that a < x < y < b
Hence x and y are required irrational numbers.
Q12. Find two irrational numbers lying between 0.1 and 0.12.
Solution: Let a = 0.1 =0.10
And b = 0.12
We observe that In the second decimal place a has digit 0 and b has digit 2.
Therefore, a < b.
So, if we consider irrational numbers
x = 0.1101101100011... y=0.111011110111110... We find that a < x < y < 0
Hence, x and y are required irrational numbers.
Q13. Prove that 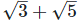 is an irrational number.
is an irrational number.
Solution: If possible, let 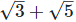 be a rational number equal to x.
be a rational number equal to x.
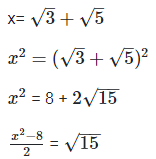
Now, 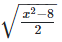 is rational
is rational
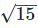 is rational
is rational
Thus, we arrive at a contradiction.
Hence,  is an irrational number.
is an irrational number.
FAQs on RD Sharma Solutions Ex-1.4, Number System, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are RD Sharma Solutions? |  |
| 2. What is Ex-1.4 in RD Sharma Solutions for Class 9? |  |
| 3. How can RD Sharma Solutions help in Class 9 Mathematics exam preparation? |  |
| 4. Are RD Sharma Solutions for Class 9 available online? |  |
| 5. Can RD Sharma Solutions for Class 9 be used for self-study purposes? |  |






















