RD Sharma Solutions Ex-13.3, (Part -1), Linear Equation In Two Variables, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1: Draw the graph of each of the following linear equations in two variables:
(i) x + y = 4
(ii) x – y = 2
(iii) -x + y = 6
(iv) y = 2x
(v) 3x + 5y = 15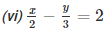
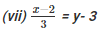
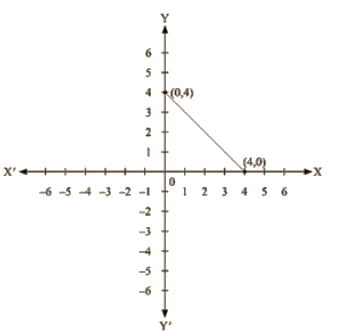
Ans. (i) We are given, x + y = 4
We get, y = 4 – x,
Now, substituting x = 0 in y = 4 – x,
we get y = 4
Substituting x = 4 in y = 4 — x, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given table
| X | 0 | 4 |
| Y | 4 | 0 |
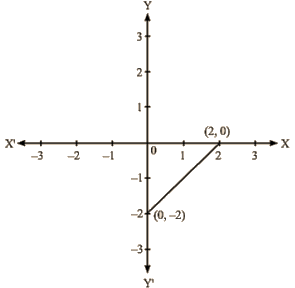
(ii) We are given, x – y = 2
We get, y = x – 2
Now, substituting x = 0 in y= x – 2, we get y = – 2
Substituting x = 2 in y = x – 2, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 2 |
| Y | -2 | 0 |
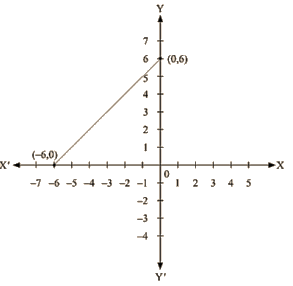
(iii) We are given, – x + y = 6
We get, y = 6 + x
Now, substituting x = 0 in y = 6 + x,
We get y =6
Substituting x = -6 in y = 6+ x, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation.
| X | 0 | -6 |
| Y | 6 | 0 |
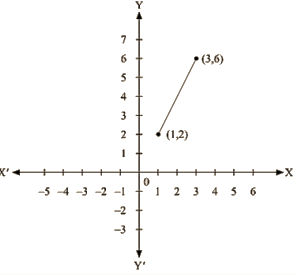
(iv) We are given, y = 2x
Now, substituting x = 1 in y = 2x
We get y = 2
Substituting x = 3 in y = 2x
We get y = 6
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 1 | 3 |
| Y | 2 | 6 |
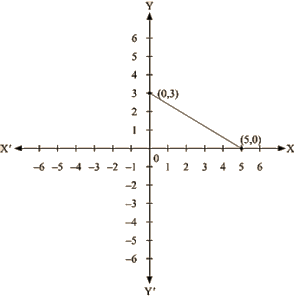
(v) We are given, 3x + 5y = 15
We get, 15 – 3x = 5y
Now, substituting x = 0 in 5y = 15 – 3x,
We get; 5y = 15
y =3
Substituting x = 5 in 5y = 15 – 3x
we get 5 y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 5 |
| Y | 3 | 0 |
(vi) we are given.
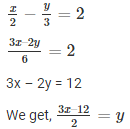
Now, substituting x = 0 in 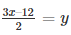
We get y = -6
Substituting x = 4 in
We get y = 0
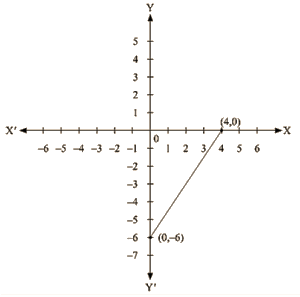
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 4 |
| Y | -6 | 0 |
(vii) We are given,
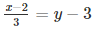
We get, x-2 = 3(Y-3)
x – 2 = 3y – 9
x = 3y – 7
Now, substituting x = 5 in x = 3y – 7,
We get; y = 4
Substituting x = 8 in x = 3y – 7 ,
We get; y = 5
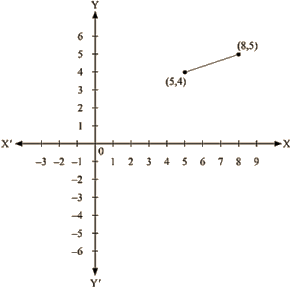
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 5 | 8 |
| Y | 4 | 5 |
(viii) We are given, 2y = – x +1
We get, 1 – x = 2Y
Now, substituting x =1 in1 – x = 2Y, we get
y = 0
Substituting x = 5 in 1 – x = 2Y , we get
y = – 2
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 1 | 5 |
| Y | 0 | -2 |
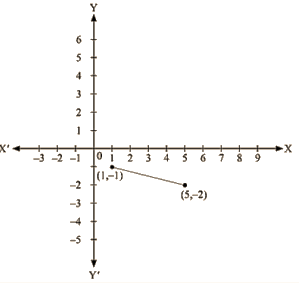
Q 2: Give the equations of two lines passing through ( 3, 12). How many more such lines are there, and why?
Ans. We observe that x = 3 and y = 12 is the solution of the following equations
4x – y = 0 and 3x – y + 3 = 0
So, we get the equations of two lines passing through (3, 12) are, 4x – y = 0 and 3x – y + 3 = 0.
We know that passing through the given point infinitely many lines can be drawn.
So, there are infinitely many lines passing through (3, 12)
Q 3 : A three-wheeler scooter charges Rs 15 for first kilometer and Rs 8 each for every subsequent kilometer. For a distance of x km, an amount of Rs y is paid. Write the linear equation representing the above information.
Ans. Total fare of Rs y for covering the distance of x km is given by
y = 15 + 8(x – 1)
y = 15 + 8x – 8
y = 8x + 7
Where, Rs y is the total fare (x – 1) is taken as the cost of first kilometer is already given Rs 15 and 1 has to subtracted from the total distance travelled to deduct the cost of first Kilometer.
Q 4 : A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Aarushi paid Rs 27 for a book kept for seven days. If fixed charges are Rs x and per day charges are Rs y. Write the linear equation representing the above information.
Ans. Total charges of Rs 27 of which Rs x for first three days and Rs y per day for 4 more days is given by
x + y ( 7 – 3 ) = 27
x + 4y = 27
Here, (7 —3) is taken as the charges for the first three days are already given at Rs x and we have to find the charges for the remaining four days as the book is kept for the total of 7 days.
Q5: A number is 27 more than the number obtained by reversing its digits. lf its unit’s and ten’s digit are x and y respectively, write the linear equation representing the statement.
Ans. The number given to us is in the form of ‘ yx ‘,
Where y represents the ten’s place of the number
And x represents the unit’s place of the number.
Now, the given number is 10y + x
Number obtained by reversing the digits of the number is 10x + y
It is given to us that the original number is 27 more than the number obtained by reversing its digits
So, 10y + x = 10x + y + 27
10y – y + x – 10x = 27
9y – 9x = 27
9 ( y – x ) = 27
y – x = 27/9 = 3
x – y + 3 = 0
Q6: The Sum of a two digit number and the number obtained by reversing the order of its digits is 121. If units and tens digit of the number are x and y respectively, then write the linear equation representing the above statement.
Ans. The number given to us is in the form of ‘ yx’ ,
Where y represents the ten’s place of the number and x represents the units place of the number
Now, the given number is 10y + x
Number obtained by reversing the digits of the number is 10x+ y
It is given to us that the sum of these two numbers is 121
So, (10y + x)+ (10x + y) = 121
10y + y + x + 10x = 121
11y + 11x = 121
11 (y + x) = 121
x + y = 121/11 = 11
x + y = 11
Q7 : Plot the Points (3,5) and (-1,3) on a graph paper and verify that the straight line passing through the points, also passes through the point (1,4)
Ans.
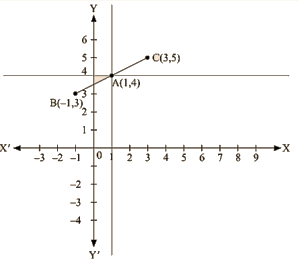
By plotting the given points (3, 5) and (-1, 3) on a graph paper, we get the line BC.
We have already plotted the point A (1, 4) on the given plane by the intersecting lines.
Therefore, it is proved that the straight line passing through (3, 5) and (-1, 3) also passes through A (1, 4).
FAQs on RD Sharma Solutions Ex-13.3, (Part -1), Linear Equation In Two Variables, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of studying linear equations in two variables in Class 9 Mathematics? |  |
| 2. How can we solve linear equations in two variables using the elimination method? |  |
| 3. Can linear equations in two variables have more than one solution? |  |
| 4. What is the graphical method of solving linear equations in two variables? |  |
| 5. How can linear equations in two variables be applied in real-life situations? |  |






















