Ex-15.2, (Part - 1), Properties Of Triangles, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Q1. Two angles of a triangle are of measures 150∘ and 30∘. Find the measure of the third angle.
Solution.
Let the third angle be x
Sum of all the angles of a triangle = 180∘
105∘+ 30∘+x = 180∘
135∘+ x = 180∘
x = 180∘ – 135∘
x = 45∘
Therefore the third angle is 45∘
Q2. One of the angles of a triangle is 130∘, and the other two angles are equal What is the measure of each of these equal angles?
Solution.
Let the second and third angle be x
Sum of all the angles of a triangle = 180∘
130∘+ x+x = 180∘
130∘+2x = 180∘
2x = 180∘– 130∘
2x = 50∘
x = 50/2
x = 25∘
Therefore the two other angles are 25∘ each
Q3. The three angles of a triangle are equal to one another. What is the measure of each of the angles?
Solution.
Let the each angle be x
Sum of all the angles of a triangle = 180∘
x+x+x = 180∘
3x = 180∘
x = 1803
x = 60∘
Therefore angle is 60∘ each
Q4. If the angles of a triangle are in the ratio 1 : 2 : 3, determine three angles.
Solution.
If angles of the triangle are in the ratio 1:2:3 then take first angle as ‘x’, second angle as ‘2x’ and third angle as ‘3x’
Sum of all the angles of a triangle = 180∘
x+2x+3x = 180∘
6x = 180∘
x = 180/6
x=30∘
2x = 30∘×2 = 60∘
3x = 30∘×3 = 90∘
Therefore the first angle is 30∘, second angle is 60∘ and third angle is 90∘
Q5. The angles of a triangle are 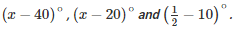 Find the value of x.
Find the value of x.
Solution.
Sum of all the angles of a triangle = 180∘
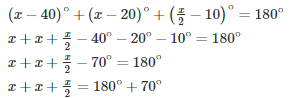
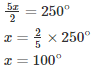
Hence we can conclude that x is equal to 100∘
Q6. The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is 10∘. Find the three angles.
Solution.
Let the first angle be x
Second angle be x+10∘
Third angle be x+10∘+ 10∘
Sum of all the angles of a triangle = 180∘
x+ x+10∘+ x+10∘+ 10∘ = 180∘
3x+30 = 180
3x = 180-30
3x = 150
x = 150/3
x = 50∘
First angle is 50
Second angle x+10∘ = 50+10 = 60∘
Third angle x+10∘+ 10∘ = 50+10+10 = 70∘
Q7. Two angles of a triangle are equal and the third angle is greater than each of those angles by 30∘. Determine all the angles of the triangle
Solution.
Let the first and second angle be x
The third angle is greater than the first and second by 30∘ = x+30∘
The first and the second angles are equal
Sum of all the angles of a triangle=180∘
x+x+x+30∘ = 180∘
3x+30 = 180
3x=180-30
3x = 150
x = 150/3
x = 50∘
Third angle = x+30∘ = 50∘+ 30∘ = 80∘
The first and the second angle is 50∘ and the third angle is 80∘
Q8. If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.
Solution.
One angle of a triangle is equal to the sum of the other two
x = y+z
Let the measure of angles be x,y,z
x+y+z = 180∘
x+x = 180∘
2x = 180∘
x = 180∘/2
x = 90∘
If one angle is 90∘ then the given triangle is a right angled triangle
Q9. If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Solution.
Each angle of a triangle is less than the sum of the other two
Measure of angles be x,y and z
x>y+z
y<x+z
z<x+y
Therefore triangle is an acute triangle
Q10. In each of the following, the measures of three angles are given. State in which cases the angles can possibly be those of a triangle:
(i) 63∘, 37∘, 80∘
(ii) 45∘, 61∘, 73∘
(iii) 59∘, 72∘, 61∘
(iv) 45∘, 45∘, 90∘
(v) 30∘, 20∘, 125∘
Solution.
(i) 63∘, 37∘, 80∘ = 180∘
Angles form a triangle
(ii) 45∘, 61∘, 73∘ is not equal to 180∘
Therefore not a triangle
(iii) 59∘, 72∘, 61∘ is not equal to 180∘
Therefore not a triangle
(iv) 45∘, 45∘, 90∘ = 180
Angles form a triangle
(v) 30∘, 20∘, 125∘ is not equal to 180∘
Therefore not a triangle
Q11. The angles of a triangle are in the ratio 3: 4 : 5. Find the smallest angle
Solution.
Given that
Angles of a triangle are in the ratio: 3: 4: 5
Measure of the angles be 3x, 4x, 5x
Sum of the angles of a triangle = 180∘
3x+4x+5x = 180∘
12x = 180∘
x = 180∘/12
x = 15∘
Smallest angle = 3x
= 3 x 15∘
= 45∘
Q12. Two acute angles of a right triangle are equal. Find the two angles.
Solution.
Given acute angles of a right angled triangle are equal
Right triangle: whose one of the angle is a right angle
Measured angle be x,x,90∘
x+x+180∘ = 180∘
2x = 90∘
x = 90∘/2
x = 45∘
The two angles are 45∘ and 45∘
Q13. One angle of a triangle is greater than the sum of the other two. What can you say about the measure of this angle? What type of a triangle is this?
Solution.
Angle of a triangle is greater than the sum of the other two
Measure of the angles be x,y,z
x>y+z or
y>x+z or
z>x+y
x or y or z>90∘ which is obtuse
Therefore triangle is an obtuse angle
Q14. AC, AD and AE are joined. Find ∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA
Solution.
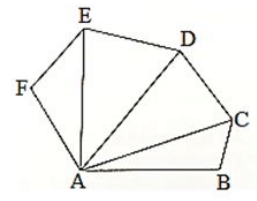
∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA
We know that sum of the angles of a triangle is 180∘
Therefore in ΔABC,we have
∠CAB+∠ABC+∠BCA = 180∘—(i)
In ΔACD,we have
∠DAC+∠ACD+∠CDA = 180∘—(ii)
In ΔADE,we have
∠EAD+∠ADE+∠DEA = 180∘—(iii)
In ΔAEF,we have
∠FAE+∠AEF+∠EFA = 180∘—(iv)
Adding (i),(ii),(iii),(iv) we get
∠CAB+∠ABC+∠BCA+∠DAC+∠ACD+∠CDA+∠EAD+∠ADE+∠DEA+∠FAE+∠AEF+∠EFA = 720∘
Therefore
∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA = 720∘
FAQs on Ex-15.2, (Part - 1), Properties Of Triangles, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are some properties of triangles? |  |
| 2. How can I determine if three given side lengths can form a triangle? |  |
| 3. What is the Pythagorean theorem and how is it used in triangles? |  |
| 4. How can I determine if two triangles are congruent? |  |
| 5. How can I find the area of a triangle? |  |

|
Explore Courses for Class 7 exam
|

|

















