Ex-15.3, (Part - 2), Properties Of Triangles, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
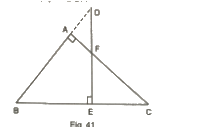
11. In Fig, ABC is a right triangle right angled at A. D lies on BA produced and DE perpendicular to BC intersecting AC at F. If ∠AFE = 130°, find
(i) ∠BDE
(ii) ∠BCA
(iii) ∠ABC
Solution.
(i)
Here,
∠BAF + ∠FAD = 180° (Linear pair)
∠FAD =180°-∠BAF =180°– 90° = 90°
Also,
∠AFE = ∠ADF + ∠FAD (Exterior angle property)
∠ADF + 90° = 130°
∠ADF = 130°−90°=40°
(ii) We know that the sum of all the angles of a triangle is 180°.
Therefore, for ΔBDE, we can say that :
∠BDE + ∠BED + ∠DBE = 180°.
∠DBE= 180°– ∠BDE ∠BED = 180°−90°−40°= 50°——(i)
Also,
∠FAD = ∠ABC + ∠ACB (Exterior angle property)
90° = 50° + ∠ACB
Or,
∠ACB = 90°– 50° = 40°
(iii) ∠ABC = ∠DBE =50° [From (i)]
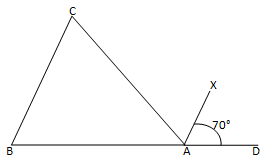
12. ABC is a triangle in which ∠B=∠C and ray AX bisects the exterior angle DAC. If ∠DAX=70°. Find ∠ACB.
Solution.
Here,
∠CAX = ∠DAX (AX bisects ∠CAD)
∠CAX =70°
∠CAX +∠DAX + ∠CAB =180°
70°+ 70° + ∠CAB =180°
∠CAB =180° –140°
∠CAB =40°
∠ACB +∠CBA + ∠CAB =180° (Sum of the angles of ΔABC)
∠ACB +∠ACB+ 40° =180° (∠C= ∠B)
2∠ACB= 180°– 40°
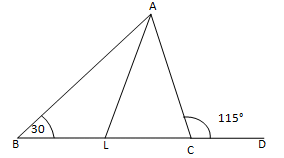
13. The side BC of ΔABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC=30°and ∠ACD=115°, find ∠ALC
Solution.
∠ACD and ∠ACL make a linear pair.
∠ACD+ ∠ACB = 180°
115° + ∠ACB =180°
∠ACB = 180°– 115°
∠ACB = 65°
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔABC, we can say that :
∠ABC + ∠BAC + ∠ACB = 180°
30° + ∠BAC + 65° = 180°
Or,

Using the above rule for ΔALC, we can say that :
∠ALC + ∠LAC + ∠ACL = 180°

Or,
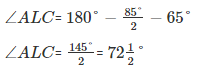
14. D is a point on the side BC of ΔABC. A line PDQ through D, meets side AC in P and AB produced at Q. If ∠A = 80°, ∠ABC = 60° and ∠PDC = 15°, find
(i) ∠AQD
(ii) ∠APD
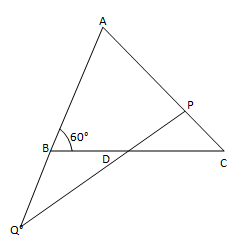
Solution.
∠ABD and ∠QBD form a linear pair.
∠ABC + ∠QBC =180°
60° + ∠QBC = 180°
∠QBC = 120°
∠PDC = ∠BDQ (Vertically opposite angles)
∠BDQ = 75°
In ΔQBD :
∠QBD + ∠QDB + ∠BDQ =180° (Sum of angles of ΔQBD)
120°+ 15° + ∠BQD = 180°
∠BQD = 180°– 135°
∠BQD=45°
∠AQD = ∠BQD = 45°
In ΔAQP:
∠QAP + ∠AQP + ∠APQ = 180° (Sum of angles of ΔAQP)
80° + 45° + ∠APQ = 180°
∠APQ= 55°
∠APD = ∠APQ
15. Explain the concept of interior and exterior angles and in each of the figures given below. Find x and y
Solution.
The interior angles of a triangle are the three angle elements inside the triangle.
The exterior angles are formed by extending the sides of a triangle, and if the side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.
Using these definitions, we will obtain the values of x and y.
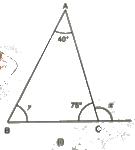
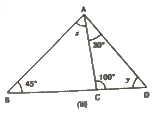
(I) From the given figure, we can see that:
∠ACB + x = 180° (Linear pair)
75°+ x = 180°
Or,
x = 105°
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔABC, we can say that :
∠BAC+ ∠ABC +∠ACB = 180°
40°+y+ 75° = 180°
Or,
y = 65°
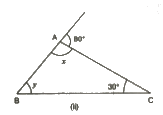
(ii)
x +80° = 180° (Linear pair)
= x = 100°
In ΔABC:
x+ y+ 30° = 180° (Angle sum property)
100° + 30° + y = 180°
= y = 50°
(iii)
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔACD, we can say that :
30° + 100° + y = 180°
Or,
y = 50°
∠ACB + 100° = 180°
∠ACB = 80° … (i)
Using the above rule for ΔACD, we can say that :
x+ 45° + 80° = 180°
= x = 55°
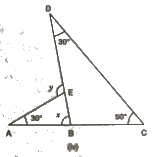
(iv)
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔDBC, we can say that :
30° + 50° + ∠DBC = 180°
∠DBC = 100°
x + ∠DBC = 180° (Linear pair)
x = 80°
And,
y = 30° + 80° = 110° (Exterior angle property)
16. Compute the value of x in each of the following figures

Solution.
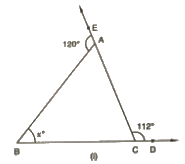
(i) From the given figure, we can say that :
∠ACD + ∠ACB = 180° (Linear pair)
Or,
∠ACB = 180°– 112° = 68°
We can also say that :
∠BAE + ∠BAC = 180° (Linear pair)
Or,
∠BAC = 180°– 120° = 60°
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔABC:
x+ ∠BAC + ∠ACB = 180°
x = 180°– 60°– 68° = 52°
= x = 52°
(ii) From the given figure, we can say that :
∠ABC + 120° = 180° (Linear pair)
∠ABC = 60°
We can also say that :
∠ACB+ 110° = 180° (Linear pair)
∠ACB = 70°
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔABC :
x+ ∠ABC + ∠ACB = 180°
= x = 50°
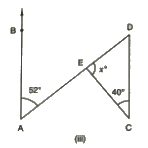
(iii)
From the given figure, we can see that :
∠BAD = ∠ADC = 52° (Alternate angles)
We know that the sum of all the angles of a triangle is 180°.
Therefore, for ΔDEC:
x + 40°+ 52° = 180°
= x = 88°
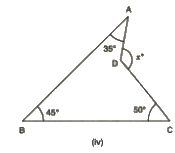
(iv) In the given figure, we have a quadrilateral whose sum of all angles is 360°.
Thus,
35° + 45° + 50° + reflex∠ADC = 360°
Or,
reflex∠ADC = 230°
230° + x = 360° (A complete angle)
= x = 130°
FAQs on Ex-15.3, (Part - 2), Properties Of Triangles, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the properties of triangles? |  |
| 2. What is the angle sum property of a triangle? |  |
| 3. How do we determine the type of triangle based on its angles? |  |
| 4. What is the triangle inequality theorem? |  |
| 5. How is the longest side of a triangle related to its largest angle? |  |





















