Ex-16.2, Congruence, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
In the following pairs of triangles (Fig. 12 to 15), the lengths of the sides are indicated along sides. By applying SSS condition, determine which are congruent. State the result in symbolic form.
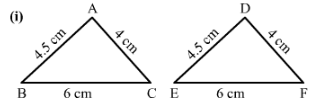
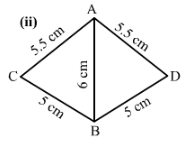
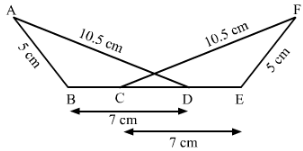
Answer 1:
1) In ΔABC and ΔDEF∆ABC and ∆DEF
AB = DE = 4.5 cm (Side)
BC = EF = 6 cm (Side)
and AC = DF = 4 cm (Side)
Therefore, by SSS criterion of congruence, △ABC≅△DEF△ABC≅△DEF.
2)
In △ACB and △ADB
AC =AD (Side)
BC = BD (Side)
and AB=AB (Side)
Therefore, by SSS criterion of congruence, △ACB≅△ADB
3)
In △ABD and △FEC,
AB = FE (Side)
AD = FC (Side)
BD = CE (Side)
Therefore, by SSS criterion of congruence, △ABD≅△FEC△ABD≅△FEC.
Question 2:
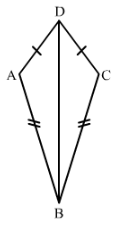
In Fig. 16, AD = DC and AB = BC.
(i) Is ∆ ABD ≅ ∆ CBD?
(ii) State the three parts of matching pairs you have used to answer (i).
Answer 2:
Yes △ABD≅△CBD△ABD≅△CBD by the SSS criterion.
We have used the three conditions in the SSS criterion as follows:
AD = DC
AB = BC
and DB = BD
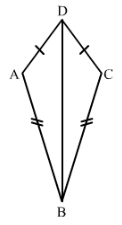
Question 3:
In Fig. 17, AB = DC and BC = AD.
(i) Is ∆ ABC ≅ ∆ CDA?
(ii) What congruence condition have you used?
(iii) You have used some fact, not given in the question, what is that?
Answer 3:
We have AB = DC
BC = AD
and AC = AC
Therefore by SSS △ABC≅△CDA.
We have used Side Side Side congruence condition with one side common in both the triangles.
Yes, we have used the fact that AC = CA.
Question 4:
If ∆ PQR ≅ ∆ EFD,
(i) Which side of ∆ PQR equals ED?
(ii) Which angle of ∆ PQR equals ∠E?
Answer 4:
△PQR ≅ △EDF
1) Therefore PR = ED since the corresponding sides of congruent triangles are equal.
2) ∠QPR = ∠FED since the corresponding angles of congruent triangles are equal.
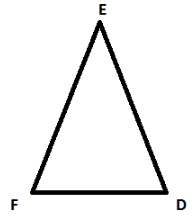
Question 5:
Triangles ABC and PQR are both isosceles with AB = AC and PQ = PR respectively. If also, AB = PQ and BC = QR, are the two triangles congruent? Which condition do you use?
If ∠B = 50°, what is the measure of ∠R?
Answer 5:
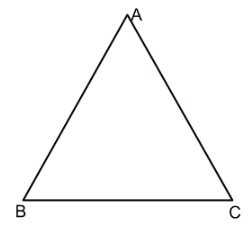
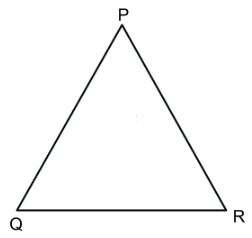
We have AB = AC in isosceles △ABC
and PQ = PR in isosceles △PQR.
Also, we are given that AB = PQ and QR = BC.
Therefore, AC = PR (AB = AC, PQ = PR and AB = PQ)
Hence, △ABC≅△PQR.
Now
∠ABC = ∠PQR (Since triangles are congruent)
However, △PQR is isosceles.
Therefore, ∠PRQ =∠PQR =∠ABC = 50°
Question 6:
ABC and DBC are both isosceles triangles on a common base BC such that A and D lie on the same side of BC. Are triangles ADB and ADC congruent? Which condition do you use? If ∠BAC = 40° and∠BDC = 100°; then find ∠ADB.
Answer 6:
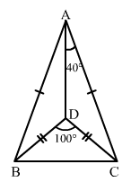
YES △ADB ≅△ADC (By SSS)
AB = AC , DB = DC AND AD= DA
∠BAD=∠CAD (c.p.c.t)
∠BAD+∠CAD=40°
2∠BAD=40°
∠BAD=40°/2=20°
∠ABC+∠BCA+∠BAC=180° (Angle sum property)
Since ΔABC is an isosceles triangle,
∠ABC=∠BCA
∠ABC+∠ABC+40°=180°
2∠ABC=180°−40°=140°
∠ABC=140°/2=70°
∠DBC+∠BCD+∠BDC=180° (Angle sum property)
Since ΔABC is an isosceles triangle,
∠DBC=∠BCD
∠DBC+∠DBC+100°=180°
2∠DBC=180°−100°=80°
∠DBC=80°/2=40°
In ΔBAD,
∠ABD+∠BAD+∠ADB=180°(Angle sum property)
30°+20°+∠ADB=180° (∠ABD=∠ABC-∠DBC)
∠ADB=180°−20°−30°
∠ADB=130°
∠ADB =130°
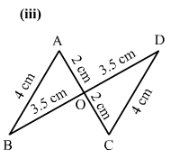
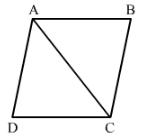
Question 7:
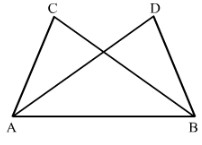
∆ ABC and ∆ ABD are on a common base AB, and AC = BD and BC = AD as shown in Fig. 18. Which of the following statements is true?
(i) ∆ ABC ≅ ∆ ABD
(ii) ∆ ABC ≅ ∆ ADB
(iii) ∆ ABC ≅ ∆ BAD
Answer 7:
In △ABC and △BAD we have,
AC = BD (given)
BC = AD (given)
and AB = BA (common)
Therefore by SSS criterion of congruency, △ABC ≅≅△BAD.
There option (iii) is true.
Question 8:
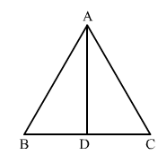
In Fig. 19, ∆ ABC is isosceles with AB = AC, D is the mid-point of base BC.
(i) Is ∆ ADB ≅ ∆ ADC?
(ii) State the three pairs of matching parts you use to arrive at your answer.
Answer 8:
We have AB = AC.
Also since D is the midpoint of BC, BD = DC.
And AD = DA.
Therefore by SSS condition, △ABD ≅△ADC△ABD ≅△ADC.
We have used AB, AC : BD, DC and AD, DA.
Question 9:
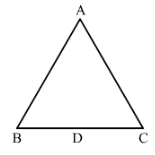
In Fig. 20, ∆ ABC is isosceles with AB = AC. State if ∆ ABC ≅ ∆ ACB. If yes, state three relations that you use to arrive at your answer.
Answer 9:
Yes △ABC ≅△ACB by SSS condition.
Since ABC is an isosceles triangle, AB = AC, BC = CB and AC = AB.
Question 10:
Triangles ABC and DBC have side BC common, AB = BD and AC = CD. Are the two triangles congruent? State in symbolic form. Which congruence condition do you use? Does ∠ABD equal ∠ACD? Why or why not?
Answer 10:
Yes.
In ΔABC and ΔDB
CAB=DB (Given)
AC=DC (Given)
BC=BC (Common)
By SSS criterion of congruency, ΔABC≅ΔDBC
No, ∠ABD and∠ACD are not equal
because AB ≠ AC.
FAQs on Ex-16.2, Congruence, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the concept of congruence in mathematics? |  |
| 2. How is congruence represented in geometric notation? |  |
| 3. What are the criteria for congruence of triangles? |  |
| 4. How do congruent figures help in solving problems in mathematics? |  |
| 5. Can congruent figures have different orientations? |  |

|
Explore Courses for Class 7 exam
|

|

















