Ex-16.5, Congruence, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
In each of the following pairs of right triangles, the measures of some parts are indicated along side. State by the application of RHS congruence condition which are congruent. State each result in symbolic form. (Fig. 46)
Answer 1:
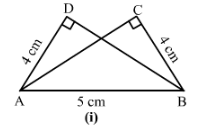
i)
∠ADC= ∠BCA =90°
AD = BC
and hyp AB = hyp AB
Therefore, by RHS, △ADB≅△ACB.
.
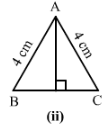
ii)
AD=AD (Common)
hyp AC = hyp AB (Given)
∠ADB+∠ADC = 180°(Linear pair)
∠ADB+90°=180°
∠ADB=180°−90°=90°
∠ADB=∠ADC = 90°
Therefore, by RHS, △ADB=△ADC
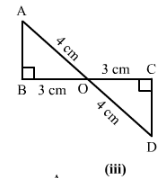
iii)
hyp AO = hyp DO
BO = CO
∠B =∠C =90°
Therefore, by RHS, △AOB≅△DOC
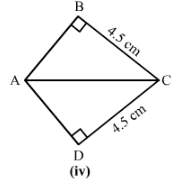
iv)
Hyp AC = Hyp CA
BC= DC
∠ABC=∠ADC = 90°
Therefore, by RHS, △ABC≅△ADC
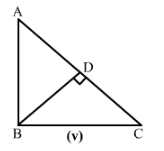
v)
BD = DB
Hyp AB =Hyp BC, as per the given figure.
∠BDA +∠BDC = 180°
∠BDA +90° = 180°
∠BDA= 180°−90°= 90°
∠BDA =∠BDC = 90°
Therefore, by RHS, △ABD≅△CBD
Question 2:
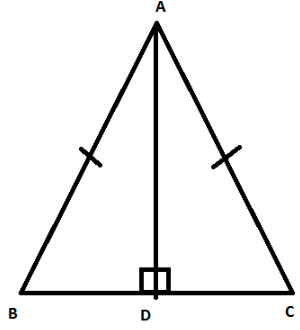
∆ ABC is isosceles with AB = AC. AD is the altitude from A on BC.
(i) Is ∆ ABD ≅ ACD?
(ii) State the pairs of matching parts you have used to answer (i).
(ii) Is it true to say that BD = DC?
Answer 2:
(i)Yes, △ABD≅△ACD△ABD≅△ACD by RHS congruence condition.
(ii) We have used Hyp AB = Hyp AC
AD = DA
and ∠ADB = ∠ADC = 90°∠ADB = ∠ADC = 90° (AD⊥BC at point D)
(iii)Yes, it is true to say that BD = DC (c.p.c.t) since we have already proved that the two triangles are congruent.
Question 3:
∆ ABC is isoseles with AB = AC. Also, AD ⊥ BC meeting BC in D. Are the two triangles ABD and ACD congruent? State in symbolic form. Which congruence condtion do you use? Which side of ∆ ADC equls BD? Which angle of ∆ ADC equals ∠B?
Answer 3:
We have AB = AC ......(1)
AD = DA (common)........(2)
and ∠ADC=∠ADB∠ADC=∠ADB (AD⊥BC at point D)........(3)
Therefore from 1, 2 and 3, by RHS congruence condition,
△ABD≅△ACD
Now, the triangles are congruent .
Therefore, BD= CD.
And ∠ABD=∠ACD (c.p.c.t).
Question 4:
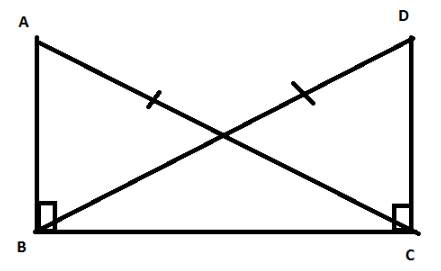
Draw a right triangle ABC. Use RHS condition to construct another triangle congruent to it.
Answer 4:
Consider
△ABC with ∠B as right angle.
We now construct another right triangle on base BC, such that ∠C is a right angle and AB = DC
Also, BC = CB
Therefore, by RHS, △ABC≅△DCB
Question 5:
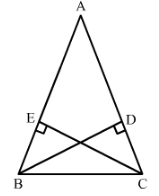
In Fig. 47, BD and CE are altitudes of ∆ ABC and BD = CE.
(i) Is ∆ BCD ≅ ∆ CBE?
(ii) State the three pairs of matching parts you have used to answer (i).
Answer 5:
(i) Yes, △BCD≅△CBE by RHS congruence condition.
(ii) We have used hyp BC = hyp CB
BD = CE (given in question)
and ∠BDC = ∠CEB =90°
FAQs on Ex-16.5, Congruence, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the importance of congruence in mathematics? |  |
| 2. How do we prove congruence between two triangles? |  |
| 3. Can two congruent triangles have different orientations or positions? |  |
| 4. What are the applications of congruence in real life? |  |
| 5. How does congruence relate to the concept of symmetry? |  |





















