Ex-22.1 (Part - 2), Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q13. Write the class size and class limits in each of the following:
(i) 104,114,124,134,144,154 and 164.
(ii) 47,52,57,62,67,72,78,82,87,92,97,102.
(iii) 12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5.
Solution 13:
(1) 104,114,124,134,144,154 and 164.
Class size = 114-104 = 10
| Class mark | Lower class limit | Upper class limit | Class limit |
| 104 | 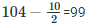 | 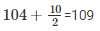 | 99-109 |
| 114 |  | 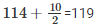 | 109-119 |
| 124 | 119 | 129 | 119-129 |
| 134 | 129 | 139 | 129-139 |
| 144 | 139 | 149 | 139-149 |
| 154 | 149 | 159 | 149-159 |
| 164 | 159 | 169 | 159-169 |
(2) 47,52,57,62,67,72,78,82,87,92,97,102.
Class size = 52-47 = 5
| Class mark | Lower class limit | Upper class limit | Class limit |
| 47 | 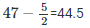 | 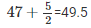 | 44.5-49.5 |
| 52 | 49.5 | 54.5 | 49.5-54.5 |
| 57 | 54.5 | 59.5 | 54.5-59.5 |
| 62 | 59.5 | 64.5 | 59.5-64.5 |
| 67 | 64.5 | 69.5 | 64.5-69.5 |
| 72 | 69.5 | 74.5 | 69.5-74.5 |
| 77 | 74.5 | 79.5 | 74.5-79.5 |
| 82 | 79.5 | 84.5 | 79.5-84.5 |
| 87 | 84.5 | 89.5 | 84.5-89.5 |
| 92 | 89.5 | 94.5 | 89.5-94.5 |
| 97 | 94.5 | 99.5 | 94.5-99.5 |
| 102 | 99.5 | 104.5 | 9.5-104.5 |
(3)12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5.
Class size = 17.5-12.5 = 5
| Class mark | Lower class limit | Upper class limit | Class limit |
| 12.5 | 12.5-2.5 = 10 | 12.5+2.5 = 15 | 10-15 |
| 17.5 | 17.5-2.5 = 15 | 17.5+2.5 = 20 | 15-20 |
| 22.5 | 22.5-2.5 = 20 | 22.5+2.5 = 25 | 20-25 |
| 27.5 | 27.5-2.5 = 25 | 27.5+2.5 = 30 | 25-30 |
| 32.5 | 32.5-2.5 = 30 | 32.5+2.5 = 35 | 30-35 |
| 37.5 | 37.5-2.5 = 35 | 37.5+2.5 = 40 | 35-40 |
| 42.5 | 42.5-2.5 = 40 | 42.5+2.5 = 45 | 40-45 |
| 47.5 | 47.5-2.5 = 45 | 47.5+2.5 = 50 | 45-50 |
Q14. Following data gives the number of children in 40 families:
1,2,6,5,1,5,1,3,2,6,2,3,4,2,0,0,4,4,3,2,2,0,0,1,2,2,4,3,2,1,0,5,1,2,4,3,4,1,6,2,2.
Represent it in the form of a frequency distribution.
Solution 14:
| Number of children | Tally marks | Number of families |
| 0 | |||| | 5 |
| 1 | |||| || | 7 |
| 2 | |||| |||| || | 12 |
| 3 | |||| | 5 |
| 4 | |||| | | 6 |
| 5 | ||| | 3 |
| 6 | ||| | 3 |
Q15. Marks scored by 40 students of class IX in mathematics are given below:
81,55,68,79,85,43,29,68,54,73,47,35,72,64,95,44,50,77,64,35,79,52,45,54,70,83,62,64,72,92,84,76,63,43,54,38,73,68,52,54.
Prepare a frequency distribution with class size of 10 marks.
Solution 15:
| Marks | Tally marks | Frequency |
| 20-30 | | | 1 |
| 30-40 | ||| | 3 |
| 40-50 | |||| | 5 |
| 50-60 | |||| ||| | 8 |
| 60-70 | |||| ||| | 8 |
| 70-80 | |||| |||| | 9 |
| 80-90 | |||| | 4 |
| 90-100 | || | 2 |
| Total = 40 |
Q16. Heights (in cm) of 30 students of class IX are given below:
155,158,154,158,160,148,149,150,153,159,161,148,157,153,157,162,159, 151, 154, 156 , 152 , 156 , 160, 152, 147, 155, 163, 155 , 157 , 153.
Prepare a frequency distribution table with 160-164 as one of the class intervals.
Solution 16:
| Height(in cm) | Tally marks | Frequency |
| 145-149 | |||| | 4 |
| 150-154 | |||| |||| | 9 |
| 155-159 | |||| |||| || | 12 |
| 160-164 | |||| | | 6 |
| Total = 30 |
Q17. The monthly wages of 30 workers in a factory are given below:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878, 840, 868, 890, 806, 840, 890.
Represent the data in the form of a frequency distribution table with class size 10.
Solution 17:
| Height(in cm) | Tally marks | Frequency |
| 800-810 | ||| | 3 |
| 810-820 | || | 2 |
| 820-830 | || | 1 |
| 830-840 | |||| ||| | 8 |
| 840-850 | |||| | 5 |
| 850-860 | | | 1 |
| 860-870 | ||| | 3 |
| 870-880 | | | 1 |
| 880-890 | | | 1 |
| 890-900 | |||| | 5 |
| Total = 30 |
Q18. The daily maximum temperatures (in degree Celsius) recorded in a certain city during the month of November are as follows:
25.8,24.5,25.6,20.7,21.8,20.5,20.6,20.9,22.3,22.7,23.1,22.8,22.9,21.7,21.3,20.5,20.9,23.1,22.4, 21.5,22.7,22.8,22.0,23.9,24.7,22.8,23.8,24.6,23.9,21.1.
Represent the data in the form of a frequency distribution table with class size 1 10CC.
Solution 18:
| Maximum temperature(in degree Celsius) | Tally marks | Frequency |
| 20.0-21.0 | |||| | | 6 |
| 21.0-22.0 | |||| | 5 |
| 22.0-23.0 | |||| |||| | 9 |
| 23.0-24.0 | |||| | 5 |
| 24.0-25.0 | ||| | 3 |
| 25.0-26.0 | || | 2 |
| Total = 30 |
Q19. Construct a frequency table with equal class intervals from the following data on the monthly wages (in rupees) of 28 laborers working in a factory, taking one of the class intervals as 210-230(230 not included).
220,268,258,242,210,268,272,242,311,290,300,320,319,304,302,218,306,292,254,278,210,240,280,316,306,215,256,236.
Solution 19:
| Monthly wages(in rupees) | Tally marks | Frequency |
| 210-230 | |||| | 4 |
| 230-250 | |||| | 4 |
| 250-270 | |||| | 5 |
| 270-290 | ||| | 3 |
| 290-310 | |||| || | 7 |
| 310.0-330.0 | |||| | 5 |
| Total = 28 |
Q20 The daily minimum temperatures in degree Celsius recorded in a certain arctic region are as follows:
-12.5,-10.8,-18.6,-8.4-10.8,-4.2,-4.8,-6.7,-13.2,-11.8,-2.3,-1.2,
-2.6,0,2.4,0,3.2,2.7,3.4,0,-2.4,-2.4,0,3.2,2.7,3.4,0,-2.4,-5.8,-8.9,-14.6,-12.3,
-11.5,-7.8,-2.9.
Represent them as frequency distribution table taking -19.9 to -15 as the first class interval.
Solution 20:
Since first class interval is -19.9 to -15, frequency distribution with lower limit included and upper limit excluded is:
| Temperature | Tally marks | Frequency |
| -19.9 to -15 | || | 2 |
| -15 to -10.1 | |||| || | 7 |
| -10.1 to -5.2 | |||| | 5 |
| -5.2 to -0.3 | |||| | 4 |
| -0.3 to -4.6 | |||| |||| |||| || | 17 |
| Total = 35 |
Q21. The blood groups of 30 students of class VIII are recorded as follows:
A,B,O,O,AB,O,A,O,B,A,O,B,A,O,O,A,AB,O,A,A,O,O,AB,B,A,O,B,A,B,O
Represent this data in the form of a frequency distribution table .Find out which is the most common and which is the most rarest blood group among these students.
Solution 21:
Here 9 students have blood group A,6 as B,3 as AB and 12 as O
So the table representing the data is as follows:
| Blood group | Number of students |
| A | 9 |
| B | 6 |
| AB | 3 |
| O | 12 |
| Total | 30 |
As 12 students have their blood group O and 3 students have their blood group as AB. Therefore the most common blood group is O and the rarest blood group is AB.
Q22. Three coins were tossed 30 times. Each time the number of heads occurring was noted down as follows:
0, 1, 2, 2, 1, 2, 3, 1, 3, 0
1, 3, 1, 1, 2, 2, 0, 1, 2, 1
3, 0, 1, 1, 2, 3, 2, 2, 0
Prepare a frequency distribution table for the data given above.
Solution 22:
By observing the data given above , the following frequency table can be constructed:
| Number of heads | Frequency |
| 0 | 6 |
| 1 | 10 |
| 2 | 9 |
| 3 | 5 |
| Total | 30 |
Q23. Thirty children were asked about the number of hours they watched TV programes in the previous week. The results were found as follows:
1, 6, 2, 3, 5, 12, 5, 8, 4, 8
10, 3, 4, 12, 2, 8, 15, 1, 17, 6
3, 2, 8, 5, 9, 6, 8, 7, 14, 2.
(i)Make a frequency distribution table for this data , taking class width 5 and one of the class intervals as 5-10.
(ii)How many children watched television for 15 or more hours a week.
Solution 23:
(i) Class intervals will be 0-5, 5-10, 10-15 …
The grouped frequency distribution table is as follows:
| Hours | Number of children |
| 0-5 | 10 |
| 5-10 | 13 |
| 10-15 | 5 |
| 15-20 | 2 |
| Total | 30 |
(ii) The number of children who watched TV for 15 or more hours a week is 2(i.e number of children in class interval 15-20).
FAQs on Ex-22.1 (Part - 2), Tabular Representation Of Statistical Data, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is tabular representation of statistical data? |  |
| 2. Why is tabular representation of statistical data important? |  |
| 3. What are the different types of tables used for tabular representation of statistical data? |  |
| 4. How to construct a frequency distribution table? |  |
| 5. What are the advantages of using tabular representation of statistical data? |  |






















